【单元测试】北师大版数学七年级上册《第1章 丰富的图形世界》单元测试卷(有答案)
展开2022-2023学年北师大新版七年级上册数学《第1章 丰富的图形世界》单元测试卷
一.选择题(共10小题,满分30分)
1.如图所示几何图形中,是棱柱的是( )
A.![]() B.
B. C.
C.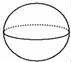 D.
D.
2.中国讲究五谷丰登,六畜兴旺,如图是一个正方体展开图,图中的六个正方形内分别标有六畜:“猪”,“牛”,“羊”,“马”,“鸡”,“狗”,将其围成一个正方体后,则与“牛”相对的是( )

A.羊 B.马 C.鸡 D.狗
3.一个四边形切掉一个角后变成( )
A.四边形
B.五边形
C.四边形或五边形
D.三角形或四边形或五边形
4.如图,几何体圆锥的面数是( )
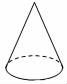
A.1 B.2 C.3 D.4
5.求圆柱形水桶能装多少升水,是求它的ㅤㅤ;制作一节圆柱形通风管要多少铁皮,是求它的ㅤㅤ.( )
A.容积、侧面积 B.容积、表面积
C.体积、表面积
6.如图是一个粉笔盒的表面展开图,若字母A表示粉笔盒的上盖,B表示侧面,则底面在表面展开图中的位置是( )
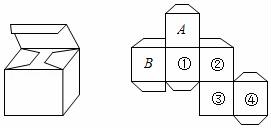
A.① B.② C.③ D.④
7.如图是一个几何体的展开图,则这个几何体是( )
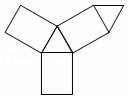
A.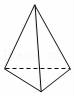 B.
B.
C.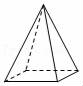 D.
D.![]()
8.一个圆柱形容器中装75.36dm3的面粉恰好装满,底面半径2dm,则容器高是( )dm.(π取3.14)
A.8 B.4 C.6 D.12
9.如图,虚线左边的图形绕虚线旋转一周,能形成的几何体是( )
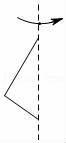
A.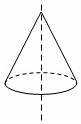 B.
B.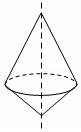
C. D.
D.
10.下列选项中,左边的平面图形能够折成右边封闭的立体图形的是( )
A.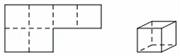
B.
C.
D.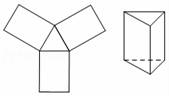
二.填空题(共10小题,满分30分)
11.如图是正方体的一种展开图,表面上的语句为北京2022年冬奥会和冬残奥会的主题口号“一起向未来!”,那么在正方体的表面与“!”相对的汉字是 .

12.一个长方体的底面是一个边长为10cm的正方形,如果高为h(cm)时,体积为V(cm3),则V与h的关系为 .
13.六个长方体包装盒按“规则方式“打包,所谓“规则方式“是指每相邻两个长方体必须以完全一样的面对接,最后得到的形状是一个更大的长方体,已知每一个小包装盒的长宽高分别为5、4、3,则按“规则方式”打包后的大长方体的表面积最小是 .

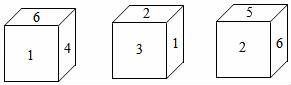
14.如图所示的几何体由 个面围成,面与面相交成 条线,其中直的线有 条,曲线有 条.
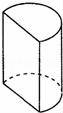
15.如图,三棱柱的底面边长都为2cm,侧棱长为5cm,则这个三棱柱的侧面展开图的面积为 .
16.小强用5个大小一样的正方形制成如图所示的拼接图形(阴影部分),若在图中只添加一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子,这样的拼接方式有 种.

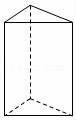
17.有一个正方体,六个面上分别写有数字1,2,3,4,5,6,如图是我们能看到的三种情况,如果记6的对面数字为a,2的对面数字为b,那么a+b的值为 .
18.用一个平面去截一个几何体,若截面是长方形,则该几何体可能是 (写三个).
19.一个n棱柱有24条棱,一条侧棱长10cm,底面的每条边长都是5cm,所有棱长的和为 cm.
20.夏天的夜晚,萤火虫飞过,在夜空中划出一条线,这蕴含的数学原理是 .
三.解答题(共7小题,满分90分)
21.一圆柱形桶内装满了水,已知桶的底面直径为a,高为b.又知另一长方体形容器的长为b,宽为a,若把圆柱形桶中的水倒入长方体形容器中(水不溢出),水面的高度是多少?
22.补画长方体(被遮住的线段用虚线表示).

23.如图所示的是一个棱柱,请问:
(1)这个棱柱由几个面围成?各面的交线有几条?它们是直的还是曲的?
(2)这个棱柱的底面和侧面各是什么形状?
(3)该棱柱有几个顶点?

24.如图所示的平面图形分别是由哪种几何体展开形成的?

(1) ;
(2) ;
(3) ;
(4) ;
(5) ;
(6) .
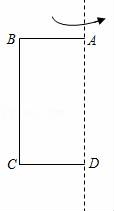
25.已知长方形的长为4cm,宽为3cm,将其绕它的一边所在的直线旋转一周,得到一个立体图形.
(1)得到的几何图形的名称为 ,这个现象用数学知识解释为 .
(2)求此几何体的体积;(结果保留π)

26.已知长方形的长为5cm,宽为4cm,将其绕它的一边所在的直线旋转一周,得到一个立体图形.
(1)得到的几何图形的名称为 ,这个现象用数学知识解释为 .
(2)求此几何体的表面积;(结果保留π)
(3)求此几何体的体积.(结果保留π)
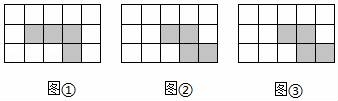
27.已知:图①,②,③均为5×3的正方形网格,在网格中选择2个空白的正方形并涂上阴影,与图中的4个阴影正方形一起构成正方体表面展开图,且3种方法得到的展开图不完全重合.
参考答案与试题解析
一.选择题(共10小题,满分30分)
1.解:A、是圆柱,故选项错误;
B、是棱柱,故选项正确;
C、是球,故选项错误;
D、是圆锥,故选项错误.
故选:B.
2.解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“猪”相对的字是“羊”;
“马”相对的字是“鸡”;
“牛”相对的字是“狗”.
故选:D.
3.解:如图可知,一个四边形截去一个角后变成三角形或四边形或五边形.

故选:D.
4.解:圆锥体是由一个底面和一个侧面围成的,
故选:B.
5.解:根据题意可得:求圆柱形水桶能装多少升水,是求它的容积;
因为圆柱形通风管只有侧面,没有底面,所以制作一节圆柱形通风管要多少铁皮就是求它的侧面积.
故选:A.
6.解:根据题意可得,
若字母A表示粉笔盒的上盖,B表示侧面,则底面在表面展开图中的位置是③.
故选:C.
7.解:侧面为3个长方形,底边为三角形,故原几何体为三棱柱.
故选:B.
8.解:设容器的高为hdm,由圆柱体的容积的计算方法得,
3.14×22×h=75.36,
解得h=6,
故选:C.
9.解:根据“面动成体”可得,旋转后的几何体为两个底面重合的圆锥的组合体,
因此选项B中的几何体符合题意.
故选:B.
10.解:A、不能折叠成正方体,故选项错误;
B、不能折成圆锥,故选项错误;
C、能折成圆柱,故选项正确;
D、不能折成三棱柱,故选项错误.
故选:C.
二.填空题(共10小题,满分30分)
11.解:对于正方体的平面展开图中相对的面一定相隔一个小正方形,由图形可知,与“!”字相对的字是“一”.
故答案为:一.
12.解:由题意得:
V=102h=100h,
故答案为:V=100h.
13.解:因为有6个长方体,6=1×6=2×3,
因此,规则方式打包有两类:“1×6”和“2×3”,
S①=2×4×5+12×5×3+12×3×4=364,
S②=4×4×5+6×3×4+12×5×3=332,
S③=4×4×5+12×3×4+6×5×3=314,
S④=6×4×5+4×3×5+6×4×6=324,
∵S①>S②>S④>S③,
还有两种情形,3×4的面折叠在一起,表面积,显然比较大,
∴最小表面积是314,
故答案为:314.
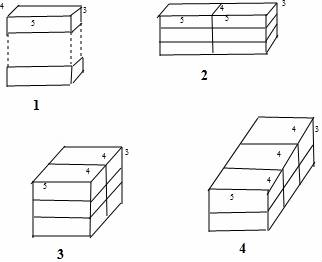
14.解:根据图形可得:如图的几何体有4个面,面与面相交成6条线,直线有4条,曲线有2条.
故答案为:4,6,4,2.
15.解:∵三棱柱的底面边长都为2cm,侧棱长为5cm,
∴此棱柱为正三棱柱,有三个侧面,且是三个全等的矩形,
∴这个三棱柱的侧面展开图的面积为:2×5×3=30(cm2),
故答案为:30cm2.
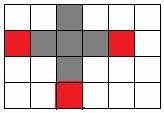
16.解:根据正方体的表面展开图可得共有3种,
如图:
17.解:根据给出的图形可得:6的对面数字为3,2的对面数字为4,
则a=3,b=4,
所以a+b的值为7;
故答案为:7.
18.解:用一个平面去截一个几何体,如果截面的形状是长方形,原来的几何体可能是长方体、正方体、圆柱.
故答案为:长方体、正方体、圆柱(答案不唯一).
19.解:∵一个n棱柱有24条棱,
∴3n=24.
∴n=8.
∴这个几何体是八棱柱,有16条底面边长,8条侧棱.
∵10×8+5×16=160(cm).
故答案为;160.
20.解:夏天的夜晚,萤火虫飞过,在夜空中划出一条线,这蕴含的数学原理是点动成线.
故答案为:点动成线.
三.解答题(共7小题,满分90分)
21.解:π×![]() ×b÷(ab)=
×b÷(ab)=![]() .
.
答:水面的高度是![]() .
.
22.解:如图所示,长方体ABCD﹣EFGH'即为所求.

23.解:(1)这个棱柱有5个面,各面的交线有9条,它们是直的;
(2)棱柱的底面是三角形,侧面是矩形;
(3)3棱柱有6个顶点.
24.解:由分析如下:
(1)正方体;
(2)长方体;
(3)三棱柱;
(4)四棱锥;
(5)圆柱;
(6)三棱柱.
故答案为:正方体;长方体;三棱柱;四棱锥;圆柱;三棱柱.
25.解:(1)长方形绕着它的一边所在的直线旋转一周,得到的立体图形是圆柱体,
故答案为:圆柱,面动成体;
(2)绕着4cm的边为轴,旋转一周所得到的是底面半径为3cm,高为4cm的圆柱体,因此体积为π×32×4=36π(cm3),
绕着3cm的边为轴,旋转一周所得到的是底面半径为4cm,高为3cm的圆柱体,因此体积为π×42×3=48π(cm3),
故答案为:36π或48π.
26.解:(1)长方形绕一边旋转一周,得圆柱,
这个现象用数学知识解释为面动成体,
故答案为:圆柱,面动成体;
(2)①以长方形的长为轴旋转,则圆柱的底面半径r=4cm,
∴圆柱的表面积为:2πrl+2πr2=2π×4×5+2π×42=72π (cm2);
②以长方形的宽为轴旋转,则圆柱的底面半径r=5cm,
∴圆柱的表面积为:2πrl+2πr2=2π×5×4+2π×52=90π (cm2).
∴圆柱的表面积为72πcm2或90πcm2;
(3)分(2)中两种情况:
①圆柱的体积为V=πr2l=π×42×5=80π( cm3);
②圆柱的体积为V=πr2l=π×52×4=100π (cm3).
∴圆柱的体积为80πcm3或100πcm3.
27.解:如图所示:(答案不唯一)