【单元测试】北师大版数学七年级上册《第5章 一元一次方程》单元测试卷（有答案）

2022-2023学年北师大新版七年级上册数学《第5章 一元一次方程》单元测试卷

一．选择题（共8小题，满分24分）

1．下列属于方程的是（　　）

A．2x＝3 B．2x＞﹣1 C．1﹣3＝﹣2 D．7y﹣1

2．若方程x+2a＝﹣3的解为x＝1，则a为（　　）

A．1 B．﹣1 C．2 D．﹣2

3．新型冠状肺炎疫情正在全球蔓延肆虐，口罩成了人们生活中必不可少的物品．某口罩厂有50名工人，每人每天可以生产800个口罩面或1000个口罩耳绳，一个口罩面需要配两个耳绳，为使每天生产的口罩刚好配套，设安排x名工人生产口罩面，则下面所列方程正确的是（　　）

A．2×1000（50﹣x）＝800x B．1000（25﹣x）＝800x 

C．1000（50﹣x）＝2×800x D．1000（50﹣x）＝800x

4．已知关于x的方程2（x+1）﹣m＝﹣2（x﹣2）与3（2x+1）＝5x﹣4的解相同，则m的值为（　　）

A．﹣30 B．30 C．﹣7 D．7

5．某轮船在两个码头之间航行，已知顺水航行需要3小时，逆水航行需要5小时，水流速度是4千米/小时，求两个码头之间的距离，若设两个码头之间的距离为x千米，则可得方程为（　　）

A． +4 B． C． D．

6．根据等式的性质，下列变形正确的是（　　）

A．若，则a＝b B．若，则3x+4x＝1 

C．若ab＝bc，则a＝c D．若4x＝a，则x＝4a

7．某商品按原价的8折出售，仍可获利20%，若商品的原价为2400元，则该商品的进价为（　　）

A．1600元 B．1640元 C．1680元 D．1860元

8．如图，已知A，B两点在数轴上，点A表示的数为﹣10，OB＝2OA，点M以每秒1个单位长度的速度从点A向右运动．点N以每秒3个单位长度的速度从点B向左运动（点M、点N同时出发）．经过几秒，点M、点N分别到原点O的距离相等？（　　）

A．5秒 B．5秒或者4秒 C．5秒或秒 D．秒

二．填空题（共10小题，满分30分）

9．方程的解为 　   　．

10．方程2x+1＝7与a﹣＝0的解相同，则a的值是 　   　．

11．写出一个解为x＝3的方程：　   　．

12．已知2xm﹣2+3＝0是关于x的一元一次方程，则m＝　   　．

13．三个连续奇数的和是57，这三个连续的奇数分别是 　   　．

14．为响应国家号召，某单位组织所有员工分x组去接种新冠疫苗加强针．若每组50人，则只有一组缺15人；若每组45人，则余下10人，根据题意，可列方程为 　   　．

15．已知：x＝4是关于x的一元一次方程3a﹣x＝+3的解，则a＝　   　．

16．甲，乙两人在一条长400米的环形跑道上跑步，甲的速度是360米/分，乙的速度是240米/分．甲在乙前面100米处，两人同时向前面跑，则甲第一次追上乙时，两人一共跑了 　   　米．

17．两块试验田去年共生产地瓜450千克，今年共生产地瓜525千克，已知第一块田的产量比去年增产16%，第二块田的产量比去年增加17%，则改良后第一块田的产量为 　   　千克．

18．某车间有22名工人，每人每天可以生产1200个螺钉或2000个螺母，1个螺钉需要配2个螺母，为使每天生产的螺钉和螺母刚好配套，若设x名工人生产螺母，则可列一元一次方程为 　   　．

三．解答题（共7小题，满分66分）

19．阅读理解；我们知道|x|的几何意义是在数轴上数x对应的点与原点的距离，即|x|＝|x﹣0|，也就是说|x|表示在数轴上数x与数0对应点之间的距离；这个结论可以推广为：|x﹣y|表示在数轴上数x、y对应点之间的距离．在解题中，我们常常运用绝对值的几何意义．

①解方程|x|＝2，容易看出，在数轴上与原点距离为2的点对应的数为±2，即该方程的解为x＝±2．

②在方程|x﹣1|＝2中，x的值就是数轴上到1的距离为2的点对应的数，所以该方程的解是x＝3或x＝﹣1．

知识运用：根据上面的阅读材料，求下列方程的解：

（1）方程|x|＝5的解；

（2）方程|x﹣2|＝3的解．

20．已知A＝2x2+mx﹣m，B＝x2+m．

（1）求A﹣2B．

（2）若x＝3是关于x的方程A﹣2B＝x+5m的解，求m的值．

21．若关于x的方程2x+5＝a的解和关于x的方程与的解相同，求字母a的值，并写出方程的解．

22．要比较a，b两个数的大小，有时可以通过比较a﹣b与0的大小来解决．

（1）如果a﹣b＞0，则a＞b．

（2）如果a﹣b＝0，则a＝b．

（3）如果a﹣b＜0，则a＜b．若x＝2a2+6b，y＝a2+2a﹣b2﹣11，试比较x，y的大小．

23．已知方程（1﹣m2）x2﹣（m+1）x+8＝0是关于x的一元一次方程．

（1）求m的值及方程的解．

（2）求代数式5x2﹣2（xm+2x2）﹣3（xm+2）的值．

24．惠民超市“十一”大酬宾，对顾客实行优惠购物，规定如下：若顾客一次性购物不超过200元，则不予优惠；若顾客一次性购物超过200元，但不超过500元，则按标价给予九折优惠；若顾客一次性购物超过500元，其中500元按上述给予九折优惠，超过500元的部分给予八折优惠．

（1）刘阿姨在该超市购买了一台标价750元的吸尘器，她应付多少元？

（2）何叔叔先后两次去该超市购物，分别付款189和554元，如果何叔叔一次性购买，只需要付款多少元？

25．在初中数学中，我们学习了各种各样的方程．以下给出了6个方程，请你把属于一元方程的序号填入圆圈（1）中，属于一次方程的序号填入圆圈（2）中，既属于一元方程又属于一次方程的序号填入两个圆圈的公共部分．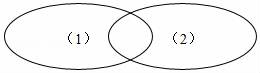

①3x+5＝9：②x2+4x+4＝0；③2x+3y＝5：④x2+y＝0；⑤x﹣y+z＝8：⑥xy＝﹣1．

参考答案与试题解析

一．选择题（共8小题，满分24分）

1．解：A、是含有未知数的等式，所以是方程，故符合题意；

B、不是等式，所以不是方程，故不符合题意；

C、是等式，但不含有未知数，所以不是方程，故不符合题意；

D、含有未知数，但不是等式，所以不是方程，故不符合题意．

故选：A．

2．解：∵方程x+2a＝﹣3的解为x＝1，

∴1+2a＝﹣3，

解得a＝﹣2．

故选：D．

3．解：设安排x名工人生产口罩面，则（50﹣x）人生产耳绳，由题意得

1000（50﹣x）＝2×800x．

故选：C．

4．解：3（2x+1）＝5x﹣4，

6x+3＝5x﹣4，

6x﹣5x＝﹣4﹣3，

x＝﹣7，

把x＝﹣7代入方程2（x+1）﹣m＝﹣2（x﹣2）得：2×（﹣7+1）﹣m＝﹣2×（﹣7﹣2），

解得：m＝﹣30，

故选：A．

5．解：设若设两个码头之间的距离为x千米，

因此可列方程为﹣4＝+4，

故选：A．

6．解：A．若，而c≠0，两边都乘以c可得a＝b，因此选项A符合题意；

B．若，两边都乘以12可得3x+4x＝12，因此选项B不符合题意；

C．当b＝0时，就不成立，因此选项C不符合题意；

D．若4x＝a，则x＝，因此选项D不符合题意；

故选：A．

7．解：设该商品的进价为x元，

则有（1+20%）x＝2400×0.8，

解得：x＝1600．

故选：A．

8．解：∵点A表示的数为﹣10，OB＝2OA，

∴点B表示的数为20，

设点M、点N运动时间是t秒，根据题意，M表示的数是﹣10+t，N表示的数是20﹣3t，

∵点M、点N分别到原点O的距离相等，

∴|﹣10+t|＝|20﹣3t|，

∴﹣10+t＝20﹣3t或﹣10+t＝﹣（20﹣3t），

解得t＝或t＝5，

故选：C．

二．填空题（共10小题，满分30分）

9．解：，

移项，得，

合并同类项，得，

系数化为1，得x＝8．

故答案为：x＝8．

10．解：2x+1＝7，

2x＝6，

x＝3，

∵方程2x+1＝7与a﹣＝0的解相同，

∴a﹣＝0，

解得a＝﹣，

故答案为：﹣．

11．解：∵方程的解为x＝3，

∴方程为x﹣3＝0，

故答案为：x﹣3＝0（答案不唯一）．

12．解：∵2xm﹣2+3＝0是关于x的一元一次方程，

∴m﹣2＝1，

解得：m＝3．

故答案为：3．

13．解：设最小一个为x，则其它两个分别是x+2，x+4，

根据题意得：x+x+2+x+4＝57，

解得x＝17，

∴x+2＝17+2＝19，x+4＝17＝4＝21，

答：这三个连续的奇数分别是17，19，21；

故答案为：17，19，21．

14．解：根据题意，可列方程为50x﹣15＝45x+10．

故答案为：50x﹣15＝45x+10．

15．解：把x＝4代入方程3a﹣x＝+3得：3a﹣4＝+3，

解得：a＝3，

故答案为：3．

16．解：设甲第一次追上乙用x分钟，则此时两人一共跑了（360+240）x米，

由题意得：（360﹣240）x＝400﹣100，

解得：x＝，

∴（360+240）x＝600×＝1500，

答：甲第一次追上乙时，两人一共跑了1500米，

故答案为：1500．

17．解：设改良前第一块田的产量为x千克，第二块田的产量为（450﹣x）千克，依题意有：

（1+16%）x+（1+17%）（450﹣x）＝525，

解得x＝150，

（1+16%）x＝1.16×150＝174．

答：改良后第一块田的产量为174千克．

故答案为：174．

18．解：由题意可得：2000x＝2×1200（22﹣x），

故答案为：2000x＝2×1200（22﹣x）．

三．解答题（共7小题，满分66分）

19．解：（1）方程|x|＝5中，x的值就是数轴上到原点的距离为5的点对应的数为±5，即该方程的解为x＝±5，

即方程|x|＝5的解是x＝5或﹣5；

（2）方程|x﹣2|＝3中x的值就是数轴上到2的距离为3的点对应的数，

∴|x﹣2|＝3的解就是x＝5或﹣1．

即方程|x﹣2|＝3的解是x1＝5，x2＝﹣1．

20．解：（1）∵A＝2x2+mx﹣m，B＝x2+m．

∴A﹣2B

＝（2x2+mx﹣m）﹣2（x2+m）

＝2x2+mx﹣m﹣2x2﹣2m

＝mx﹣3m；

（2）∵x＝3是关于x的方程A﹣2B＝x+5m的解，A﹣2B＝mx﹣3m，

∴3m﹣3m＝3+5m，

解得：m＝﹣．

21．解：2x+5＝a，

2x＝a﹣5，

x＝，

，

2（x﹣4）﹣12＝3（a﹣1），

2x＝3a+17，

x＝，

由题意得：

＝，

解得：a＝﹣11，

∴x＝＝﹣8，

∴字母a的值为﹣11，方程的解为x＝﹣8．

22．解：由于x﹣y＝2a2+6b﹣（a2+2a﹣b2﹣11）＝a2﹣2a+b2+11＝（a﹣1）2+b2+10＞0，即x﹣y＞0．

所以x＞y．

23．解：（1）∵方程（1﹣m2）x2﹣（m+1）x+8＝0是关于x的一元一次方程，

∴1﹣m2＝0且﹣（m+1）≠0，

∴m＝1，

原一元一次方程化为：﹣2x+8＝0，解得x＝4；

（2）∵5x2﹣2（xm+2x2）﹣3（xm+2）

＝5x2﹣2x﹣4x2﹣x﹣6

＝x2﹣3x﹣6，

当x＝4时，原式＝42﹣4×3﹣6＝﹣2，

即代数式5x2﹣2（xm+2x2）﹣3（xm+2）的值是﹣2．

24．解：（1）依题意得：

500×0.9+（750﹣500）×0.8

＝450+250×0.8

＝450+200

＝650（元）．

答：应付674元；

（2）设第一次优惠前应付款x元，第二次优惠前应付款y元，依题意得：

0.9x＝189，0.9×500+（y﹣500）×0.8＝554，

解得：x＝210，y＝630，

则如一次性购买应付款为：

500×0.9+（210+630﹣500）×0.8

＝450+272

＝722（元）．

答：何叔叔一次性购买，只需要付款722元．

25．解：（1）一元方程，①3x+5＝9②x2+4x+4＝0；

（2）一次方程①3x+5＝9⑤x﹣y+z＝8③2x+3y＝5；

（3）既属于一元方程又属于一次方程的是①3x+5＝9．