【单元测试】北师大版数学七年级上册《第1章 丰富的图形世界》单元测试卷2(有答案)
展开2022-2023学年北师大新版七年级上册数学《第1章 丰富的图形世界》单元测试卷
一.选择题(共10小题,满分30分)
1.把一个圆锥完全浸没在一个底面半径为r的圆柱形容器里,此时水位上升的高度为h,则这个圆锥的体积是( )
A.π•r2h B.![]() h C.2π•r2h D.3π•r2h
h C.2π•r2h D.3π•r2h
2.若圆柱的底面半径为3,母线长为5,则这个圆柱的侧面积为( )
A.15 B.12π C.15π D.30π
3.图2是图1中长方体的三视图,若用S表示面积,且S主视图=x2+2x,S![]() ,则S俯视图=( )
,则S俯视图=( )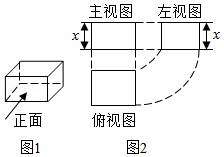
A.x2+4x+3 B.2x2+4x C.x2+2x+1 D.x2+3x+2
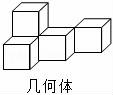
4.由5个大小相同的小正方体搭成的几何体如图所示,它的主视图是( )
A.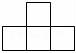 B.
B.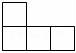 C.
C.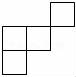 D.
D.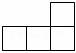
5.襄阳牛杂面因襄阳籍航天员聂海胜的一句“最想吃的还是我们襄阳的牛杂面”火爆出圈,引发了全国人民的聚焦和关注.襄阳某品牌牛杂面的包装盒及对应的立体图形如图所示,则该立体图形的主视图为( )

A. B.
B.![]()
C.![]() D.
D.
6.长方形长5厘米,宽3厘米,以宽为轴旋转一周得到圆柱的体积是( )立方厘米.
A.225.5 B.235.5 C.245.5 D.255.5
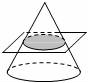
7.如图,用一个平行于圆锥底面的平面截圆锥,截面的形状是( )
A.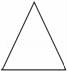 B.
B.
C.![]() D.
D.
8.下列图形中,( )是正方体的展开图.
A.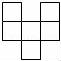 B.
B.![]()
C.![]() D.
D.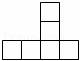
9.如图,裁掉一个正方形后能折叠成正方体,但不能裁掉的是( )
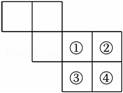
A.① B.② C.③ D.④
10.如图是正方体的表面展开图,每个面内都分别写有一个字,则与“创”字相对面上的字是( )
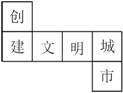
A.文 B.明 C.城 D.市
二.填空题(共10小题,满分30分)
11.一个圆柱形纸筒,它的底面直径4cm,高12cm,这个圆柱的体积是 cm3.
12.有6个棱长为1的小正方体,把它们拼成一个大的长方体,那么这个长方体的表面积为 .
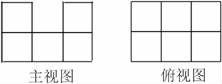
13.用几个小正方体指一个几何体,使它的主视图和俯视图如图所示,则需要的小正方体个数最少为 .
14.圆柱的侧面展开图是一个长6cm,宽4cm长方形,则这个圆柱的底面半径是 cm.(结果保留π)
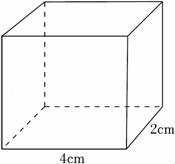
15.如图所示,水平放置的长方体的底面是长为4cm、宽为2cm的长方形,它的主视图的面积为16cm2,则长方体的体积等于 cm3.
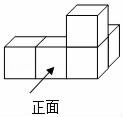
16.如图是由五个棱长均为1的正方体搭成的几何体,则从左面看到图形的面积为 .
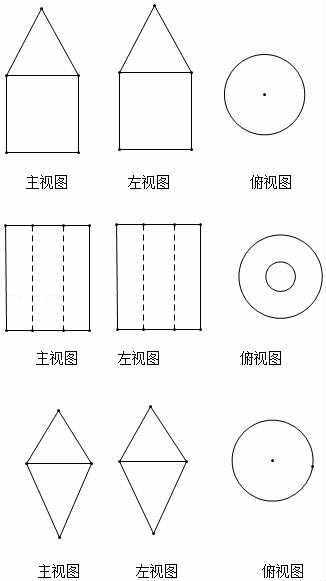
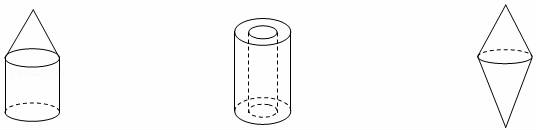
17.如图平面图形绕轴旋转一周,得到的立体图形分别是 .
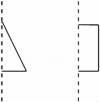
18.如图所示的A、B、C、D四个位置的某个正方形与实线部分的五个正方形组成的图形,不能拼成正方体的是位置 .
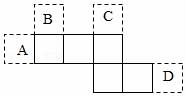
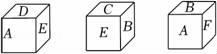
19.如图,一个正方体的六个面分别标有A、B、C、D、E、F,从三个不同方向看到的情况如图所示,则B的对面应该是字母 .
20.把高12分米的圆柱切成两段,表面积增加40平方厘米,原来圆柱的体积是 立方厘米.
三.解答题(共7小题,满分90分)
21.“数学活动”(课本第17页):做一个底面积为100cm2,长、宽、高的比分别为5:4:3的长方体.求:
(1)这个长方体的长、宽、高分别是多少?
(2)长方体的体积是多少?
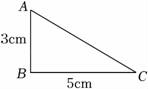
22.把三角形ABC沿BC边和AB边分别旋转一周,得到2个圆锥(如图),哪个圆锥的体积大?
23.一个几何体的三种视图如图所示.
(1)这个几何体的名称是 .
(2)求这个几何体的体积.(结果保留π)
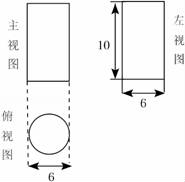
24.如图是一块长为35cm的长方体木块,点M把棱AB分成2:3的两段,过点M按平行于平面ADHE的方向把长方体切成两块后,表面积增加了800cm2,问:这两块长方体的体积分别是多少立方厘米?
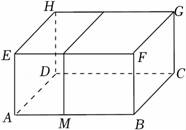
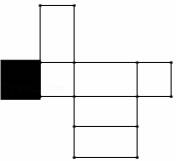
25.如图,小华用若干个正方形和长方形准备拼成一个长方体的展开图.拼完后,小华看来看去总觉得所拼图形似乎存在问题.
(1)请你帮小华分析一下拼图是否存在问题,若有多余块,则把图中多余部分涂黑;若还缺少,则直接在原图中补全;
(2)若图中的正方形边长为2cm,长方形的长为3cm,宽为2cm,求出修正后所折叠而成的长方体的体积.
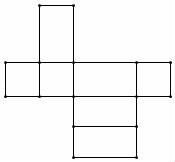
26.现有甲、乙两个圆柱体容器如图所示,甲容器的直径是10厘米,高是40厘米;乙容器的直径是20厘米,高是15厘米.若先在甲容器中倒满水,然后将其倒入乙容器中,则倒完以后,乙容器中的水面离容器口有多少厘米?(容器壁厚度忽略不计)
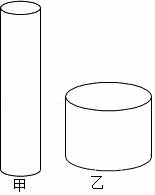
27.画出图中几何体的三视图:
参考答案与试题解析
一.选择题(共10小题,满分30分)
1.解:圆锥的体积就是圆柱体中水上升的体π•r2h.
故选:A.
2.解:根据侧面积公式可得:π×2×3×5=30π,
故选:D.
3.解:∵S主视图=x2+2x=x(x+2),S左视图=x2+x=x(x+1),
∴俯视图的长为x+2,宽为x+1,
则俯视图的面积S俯=(x+2)(x+1)=x2+3x+2.
故选:D.
4.解:从正面看,底层是三个小正方形,上层的左边是一个小正方形,
故选:B.
5.解:从正面看,是一个矩形,
故选:A.
6.解:由题意可知,圆柱体的底面半径为5厘米,高为3厘米,
所以体积为π×52×3=75π≈235.5(立方厘米),
故选:B.
7.解:用一个平行于圆锥底面的平面截圆锥,截面的形状是圆,
故选:B.
8.解:根据正方体展开图的11种特征分析,
图B是“3﹣3”型结构是正方体的展开图,
图A、图C、图D不符合正方体的展开图特征,不是正方体的展开图,
故选:B.
9.解:如图,裁掉一个正方形后能折叠成正方体,但不能裁掉的是①,
故选:A.
10.解:将正方体的表面展开图还原成正方体,以“文”字为底,则左边的是“建”字,右边的是“明”字,上面的是“城”字,正面的是“市”字,后面的是“创”字,可知“创”字与“市”字相对.
故选:D.
二.填空题(共10小题,满分30分)
11.解:圆柱的体积是V=Sh=π×22×12=48πcm3.
故答案为:48π.
12.解:第一种拼法是6个排成一排,其表面积为2+4×6=26;
第二种是6个排成两行,上下各3个,其表面积为3×6+2×2=22.
故答案为:22或26.
13.解:由俯视图可得最底层有6个小正方体,
由主视图可得第一列和第三列都有2个正方体,
那么最少需要6+2=8个正方体.
故答案为:8个.
14.解:当长6cm是底面圆的周长时,
根据圆的周长公式:l=2πr,
底面圆的半径为:6÷2÷π=![]() cm;
cm;
当宽4cm是底面圆的周长时,
根据圆的周长公式:l=2πr,
底面圆的半径为:4÷2÷π=![]() cm;
cm;
故答案为:![]() 或
或![]() .
.
15.解:依题意,得长方体的体积=16×2=32cm3.
故答案为:32.
16.解:从左边看,底层是两个小正方形,上层的右边是一个小正方形,
因为每个小正方形的面积为1,所以则它的左视图的面积为3.
故答案为:3.
17.解:由“面动成体”可知,将直角三角形绕着一条直角边旋转一周,所得到的几何体是圆锥体,
将长方形绕着一条边旋转一周,所得到的的几何体是圆柱体,
故答案为:圆锥、圆柱.
18.解:正方形A与实线部分的五个正方形组成的图形出现重叠的面,所以不能围成正方体.
故答案为:A.
19.解:由第二个图可得:
B与C,E是相邻的,
由第三个图可得:
B与A,F是相邻的,
所以,B的对面应该是字母D,
故答案为:D.
20.解:12分米=120厘米,
由题意得:
圆柱的底面积为:40÷2=20(cm2),
圆柱的体积为:20×120=2400(cm3),
故答案为:2400.
三.解答题(共7小题,满分90分)
21.(1)设长方体的长为5x cm,则宽为4x cm,高为3x cm,
由题意可得5x×4x=100,
解得x=![]() ,
,
则5x=5![]() ,4x=4
,4x=4![]() ,3x=3
,3x=3![]() .
.
答:这个长方体的长、宽、高分别是5![]()
![]() cm,4
cm,4![]()
![]() cm,3
cm,3![]()
![]() cm.
cm.
(2)5![]() ×4
×4![]() ×3
×3![]() =300
=300![]() (cm3).
(cm3).
答:长方体的体积是300![]()
![]() cm3.
cm3.
22.解:以AB边为轴旋转一周,得到圆锥体的体积为:![]() π×52×3=25π(cm3).
π×52×3=25π(cm3).
以CB边为轴旋转一周,得到圆锥体的体积为:![]() π×32×5=15π(cm3)
π×32×5=15π(cm3)
答:以AB边为轴旋转成圆锥的体积大.
23.解:(1)这个几何体是圆柱.
故答案为:圆柱;
(2)观察三视图知:该圆柱的高为10,底面直径为6,
所以其体积为:π×(![]() )2×10=90π.
)2×10=90π.
故这个几何体的体积为90π.
24.解:点M把棱AB分成1:2的两段,则可得:AM=35×![]() =14(厘米),则BM=35﹣14=21(厘米),
=14(厘米),则BM=35﹣14=21(厘米),
800÷2=400(平方厘米),
400×14=5600(立方厘米),
400×21=8400(立方厘米),
答:这两块长方体的体积分别是5600立方厘米、8400立方厘米.
25.解:(1)拼图存在问题,多了,如图:
(2)由题意得,围成的长方体长,宽,高分别为2,2,3,
∴体积为:2×2×3=12(cm3).
26.解:设倒完以后,乙容器中的水面离容器口有x cm,
则:π×(10÷2)2×40=π×(20÷2)2×(15﹣x),
解得:x=5,
答:乙容器中的水面离容器口有5 cm.
27.解:三视图,如图所示: