





- 人教版初中数学九年级上册22.1.4 第2课时《用待定系数法求二次函数的解析式》课件+教案+同步作业(含教学反思) 课件 2 次下载
- 人教版初中数学九年级上册22.2《二次函数与一元二次方程》课件+教案+同步作业(含教学反思) 课件 2 次下载
- 人教版初中数学九年级上册22.3 第2课时《实际问题与二次函数——商品利润》课件+教案+同步作业(含教学反思) 课件 3 次下载
- 人教版初中数学九年级上册22.3 第3课时《实际问题与二次函数——拱桥问题和运动中的抛物线》课件+教案+同步作业(含教学反思) 课件 2 次下载
- 人教版初中数学九年级上册 第22章《二次函数 小结与复习》课件+教案+同步检测(含教学反思) 课件 4 次下载
初中数学人教版九年级上册22.3 实际问题与二次函数教学ppt课件
展开22.3 实际问题与二次函数
第1课时 二次函数与图形面积 教学设计
![]()
在学习实际问题与二次函数之前,学生已经学习了二次函数的图象和性质,这为过渡到本节内容的学习起到了铺垫作用.教材中二次函数的应用设计了3个例题,故教学设计时把它分为二次函数与图形面积、二次函数与商品利润和实物抛物线3个课时,本课时研究二次函数与图形面积的相关内容.教学中通过掌握求最大值这一类问题,注意让学生学会用建模的思想去解决其他和函数有关的应用问题.
![]()
课题 | 22.3 第1课时 二次函数与图形面积 | 授课人 |
|
素养目标 | 1.通过图形的面积关系列出函数解析式;.用二次函数的知识分析解决有关面积的实际问题;体会二次函数是刻画现实世界的有效模型. 2.从“数”(解析式)和“形”(图象)的角度理解二次函数与实际生活中“最值”问题之间的联系,体会“数形结合”的思想.通过转化建模,会用数学的思维思考现实世界. | ||
教学重点 | 用二次函数的知识分析解决有关面积的实际问题. | ||
教学难点 | 通过图形的面积关系列出函数解析式. | ||
授课类型 | 新授课 | 课时 |
|
![]()
教学步骤 | 师生活动 | 设计意图 |
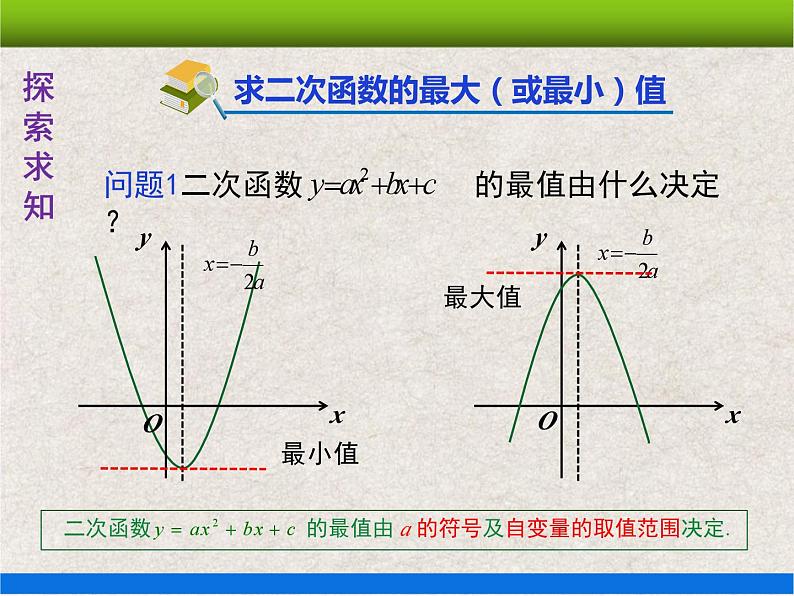
复习回顾 | 1.想一想:二次函数的常见形式有哪些? 二次函数y=ax2+bx+c(a≠0)的图象的顶点坐标是(-,),对称轴是直线x=-;二次函数y=ax2+bx+c(a≠0)的图象是一条抛物线,当a>0时,图象开口向上,当a<0时,图象开口向下. 2.通过配方求下列二次函数的最大值或最小值. (1)y=x2-6x; (2)y=-3x2+6x-1. 师生活动:学生自主进行解答,教师做好指导和点评. 提示:求解二次函数的最值一般有两种方法: 一是把一般式化为顶点式;二是利用顶点坐标公式求解. (1)y=x2-6x=(x-3)2-9,当x=3时,y有最小值-9. (2)y=-3(x-1)2+2,当x=1时,y有最大值2. | 通过回顾二次函数的最值问题,为讲解新课作铺垫,两种求解方法为学生深刻理解知识提供理论支持. |
活动一:创设情境、导入新课 | 【课堂引入】 问题:用总长为60 m的篱笆围成矩形场地,矩形场地的面积S随一边长l的变化而变化,当l是多少米时,矩形场地的面积S最大? 师生活动: 1.教师引导学生分析与矩形面积相关的量. 2.教师设问,如何用含l的代数式表示与其相邻的边的长度. 3.学生自主列函数解析式,并进行整理,讨论问题解答的正确性. 4.针对问题要求进行求解,并回答问题. 教师关注: 1.学生能否根据矩形的面积公式列函数解析式; 2.学生能否根据以前所学知识准确求出函数的最大值. | 通过实际应用,激发学生解答的欲望,让学生在合作中学习,共同解答问题,培养学生的探究能力和合作意识. |
活动二:实践探究、交流新知 | 1.探究新知 活动一:针对【课堂引入】的问题进行探究,教师总结解题过程. 师生活动: (1)确定解题的步骤:先表示矩形的长和宽,再利用面积公式列解析式,最后求最值. (2)解答过程:矩形场地的一边长为l m,则另一边长为(30-l)m, 所以矩形场地的面积S=l(30-l)=-l2+30l(0<l<30). 当l=-=15时,S有最大值=225. 也就是说,当l=15 m时,矩形场地的面积S最大. 2.师生总结 教师指导学生总结解答问题的方法和步骤,学生代表进行说明,全班互相交流,师生共同确定解题思路: (1)表示与面积相关的量.(2)利用面积公式列函数解析式,并进行整理.(3)确定自变量的取值范围.(4)利用公式求出最值. | 通过典型问题的设计和解答,让学生体会函数模型在解决实际问题中的作用. |
活动三:开放训练、体现应用 | 【典型例题】 例 如图,用长为6 m的铝合金条制成一个“日”字形窗框,已知窗框的宽为x m,窗户的透光面积为y m2(铝合金条的宽度不计). (1)求出y与x的函数关系式.
解:(1)由题意,得长为 m. ∴y=x·=-x2+3x(0<x<2). (2)由(1)可知,y和x是二次函数关系. ∵a=-<0,∴函数有最大值. ∴当x=-=1时,y最大=,此时=. 答:窗框的长和宽分别为 m和1 m时,窗户的透光面积最大,此时的最大面积为 m2. 师生活动:学生自主进行解答,教师巡视、指导、点评. 【变式训练】
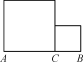
A.当C是AB的中点时,S最小 B.当C是AB的中点时,S最大 C.当C为AB的三等分点时,S最小 D.当C是AB的三等分点时,S最大 | 典型例题的设置是让学生跟着解题思路去解题,从而提高学生对二次函数与图形面积的应用能力.变式训练是对题目类型的补充. |
活动四:课堂检测 | 【课堂检测】 1.为搞好环保,某公司准备修建一个长方体的污水处理池,池底矩形的周长为100 m,则池底的最大面积是(B) A.600 m2 B.625 m2 C.650 m2 D.675 m2
则所围成矩形ABCD的最大面积是(C) A.60 m2 B.63 m2 C.64 m2 D.66 m2 3.手工课上,小明准备做一个形状是菱形的风筝,这个菱形的两条对角线长度之和恰好为60 cm,菱形的面积S(单位:cm2)随其中一条对角线的长x(单位: cm)的变化而变化. (1)请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围). (2)当x是多少时,菱形风筝面积S最大?最大面积是多少? 解:(略) | 针对本课时的主要问题,从多个角度、分层次进行检测,达到学有所成、了解课堂学习效果的目的. |
课堂小结 | 1.课堂小结: 你在本节课中有哪些收获?有哪些进步?还有哪些困惑?请谈一谈. 教师强调:(1)主要学习了如何将实际问题转化为数学问题,特别是如何利用二次函数的有关性质解决实际问题的方法. (2)利用二次函数解决实际问题时,根据面积公式等关系写出二次函数解析式是解决问题的关键. 2.布置作业: 教材第52页习题22.3第4,6题. | 课堂小结的设置能够让学生养成归纳课堂重点的习惯,提高学生的学习能力. |
板书设计 | 22.3 实际问题与二次函数 第1课时 二次函数与图形面积 解题方法: (1)用自变量表示与面积相关的量.(2)利用面积公式列函数解析式,并进行整理.(3)确定自变量的取值范围.(4)利用顶点坐标公式求出问题中最大面积. | 提纲挈领,重点突出. |
教学反思 | 二次函数是描述现实世界变量之间关系的重要模型,也是某些单变量最优化的数学模型,如最大利润、最大面积等实际问题,因此本课时主要结合这两类问题进行了一些探讨.生活中的最优化问题通过数学模型可抽象为二次函数的最值问题,由于学生对于这一转化过程较难理解,因此教学时教师可通过分步设问的方式让学生逐层深入、稳步推出,让学生自主建立数学模型,在这个过程中教师可通过让学生画图探讨最值.总之,在本课时的教学过程中,要让学生经历数学建模的基本过程,体验探究知识的乐趣.
| 反思教学过程和教师表现,进一步优化操作流程和提升自身素质. |
实际问题与二次函数PPT课件免费下载: 人教版初中数学九年级上册课文《实际问题与二次函数》,完整版PPT课件免费下载,优秀PPT背景图搭配,精美的免费ppt模板。轻松备课,欢迎免费下载使用。
初中人教版22.3 实际问题与二次函数集体备课ppt课件: 这是一份初中人教版22.3 实际问题与二次函数集体备课ppt课件,共14页。PPT课件主要包含了来到商场,我来当老板,牛刀小试,创新学习,解这类题目的一般步骤等内容,欢迎下载使用。
人教版九年级上册22.3 实际问题与二次函数教学演示课件ppt: 这是一份人教版九年级上册22.3 实际问题与二次函数教学演示课件ppt,共13页。PPT课件主要包含了一般步骤等内容,欢迎下载使用。