初中数学人教版九年级上册22.3 实际问题与二次函数教学演示ppt课件

这是一份初中数学人教版九年级上册22.3 实际问题与二次函数教学演示ppt课件，共21页。PPT课件主要包含了探究2，解如图，建立坐标系，设函数解析式为，怎样求解析式，-2-2，3问题求解等内容，欢迎下载使用。

何时窗户通过的光线最多
某建筑物的窗户如图所示,它的上半部是半圆,下半部是矩形,制造窗框的材料总长(图中所有的黑线的长度和)为15m.当x等于多少时,窗户通过的光线最多(结果精确到0.01m)?此时,窗户的面积是多少?
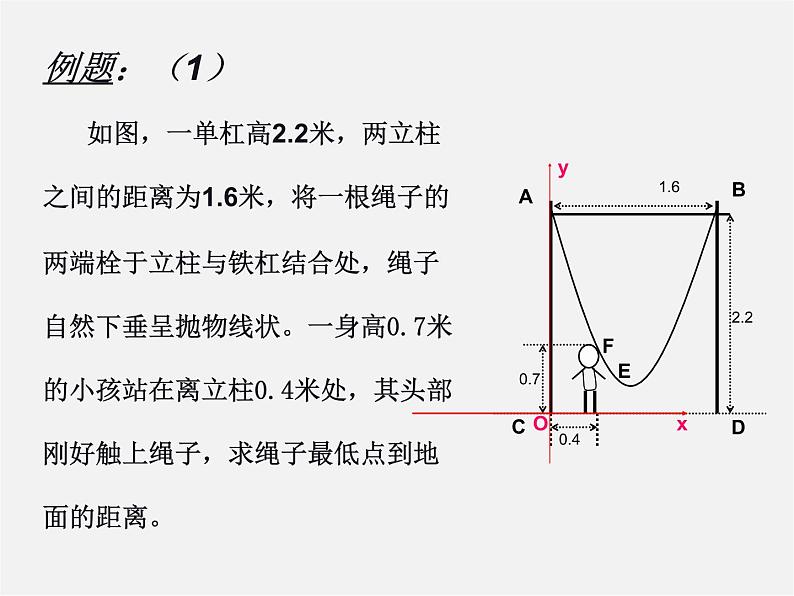
例题：（1） 如图，一单杠高2.2米，两立柱之间的距离为1.6米，将一根绳子的两端栓于立柱与铁杠结合处，绳子自然下垂呈抛物线状。一身高0.7米的小孩站在离立柱0.4米处，其头部刚好触上绳子，求绳子最低点到地面的距离。
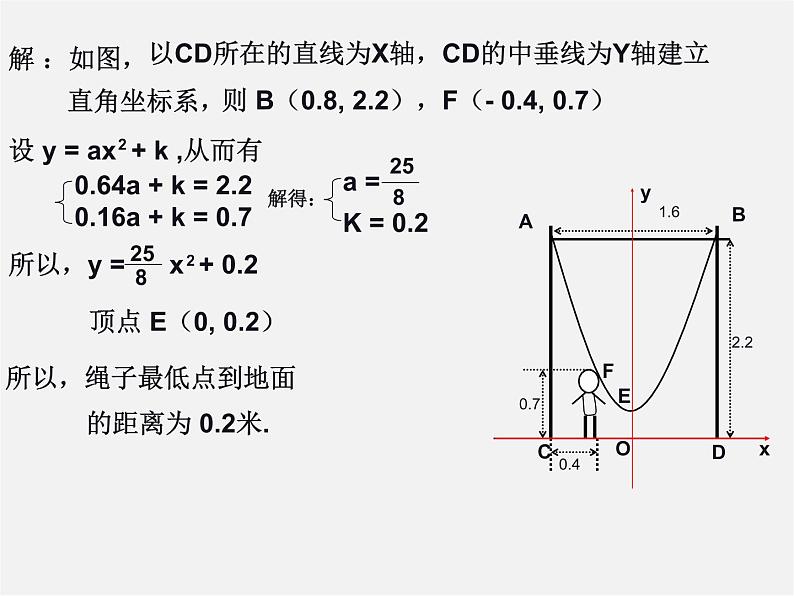
所以，绳子最低点到地面 的距离为 0.2米.
以CD所在的直线为X轴，CD的中垂线为Y轴建立 直角坐标系，
则 B（0.8, 2.2），F（- 0.4, 0.7）
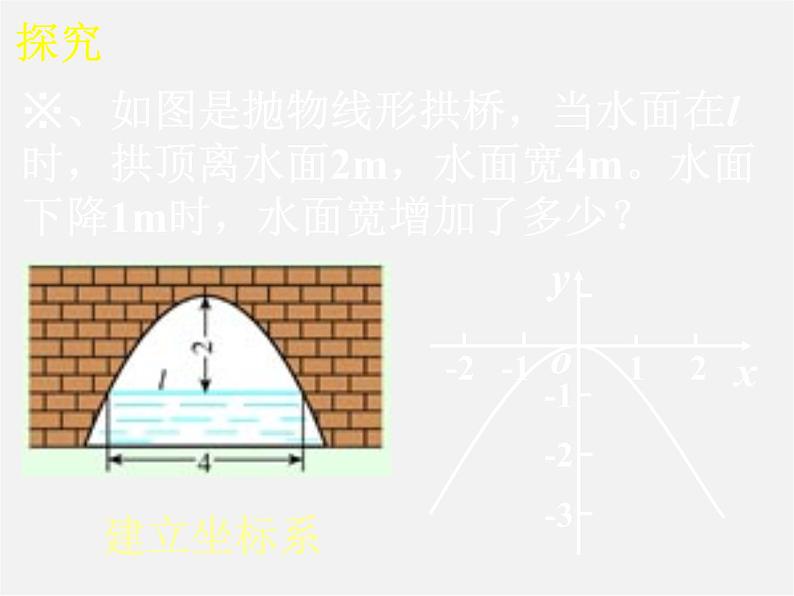
※、如图是抛物线形拱桥，当水面在l时，拱顶离水面2m，水面宽4m。水面下降1m时，水面宽增加了多少？
用函数解实际问题的一般步骤：
(1)建立平面直角坐标系；
(2)根据题意构建二次函数图象；
(4)找出实际问题的答案。
例1、如图，一座隧道的截面由抛物线和长方形构成。长方形的长OC为8m，宽AO为2m，隧道最高点P位于AB的中央且距地面6m，建立如图所示的坐标系。(1)求抛物线的解析式；
例1、如图，一座隧道的截面由抛物线和长方形构成。长方形的长OC为8m，宽AO为2m，隧道最高点P位于AB的中央且距地面6m，建立如图所示的坐标系。(2)一辆货车高4m，宽2m，能否从隧道通过？为什么？
例1、如图，一座隧道的截面由抛物线和长方形构成。长方形的长OC为8m，宽AO为2m，隧道最高点P位于AB的中央且距地面6m，建立如图所示的坐标系。(3)如果隧道内设双行道，那么这辆货车是否能顺利通过？为什么？
1、有一抛物线型的立交桥，桥的最大高度为16m，跨度为40m。现把它的图形放在平面直角坐标系里，如图所示，若在里跨度中点M5m处垂直竖立一铁柱支撑拱顶，该铁柱硬取多长？
2、如图，有一块铁皮，拱形边缘呈抛物线状，MN=4cm，顶点到MN的距离是4cm。要在铁皮上截下一矩形ABCD，使矩形顶点B、C落在MN上，A、D落在抛物线上，问这样截下的矩形铁皮的周长是否能等于8cm？
例2、如图，抛物线 经过A(1，0)、B(5，0)、C(0，5)三点。(1)求函数解析式；(2)若过点C的直线 与抛物线相交于点E(4，m)，请求出△CBE的面积S的值。
例2、如图，抛物线 经过A(1，0)、B(5，0)、C(0，5)三点。(3)在抛物线上取一点P0，使得△ABP0为等腰三角形并写出P0的坐标；
例2、如图，抛物线 经过A(1，0)、B(5，0)、C(0，5)三点。(4)除(3)中所求的P0点外，在抛物线上是否还存在其他的点P，使得△ABP为等腰三角形？若存在，请求出一共几个满足条件的点P；若不存在，请说明理由。
3、如图，抛物线 经过△ABC的三个顶点，BC∥x轴，点A在x轴上，点C在y轴上，AC=BC。(1)求出抛物线的对称轴；(2)写出A、B、C的坐标，求出抛物线的解析式；
3、如图，抛物线 经过△ABC的三个顶点，BC∥x轴，点A在x轴上，点C在y轴上，AC=BC。(3)探究：若点P是抛物线对称轴上且在x轴下方的动点，是否存在△PAB是等腰三角形？若存在，求出所有符合条件的点P坐标；若不存在，请说明理由。