





初中数学人教版九年级上册21.1 一元二次方程说课课件ppt
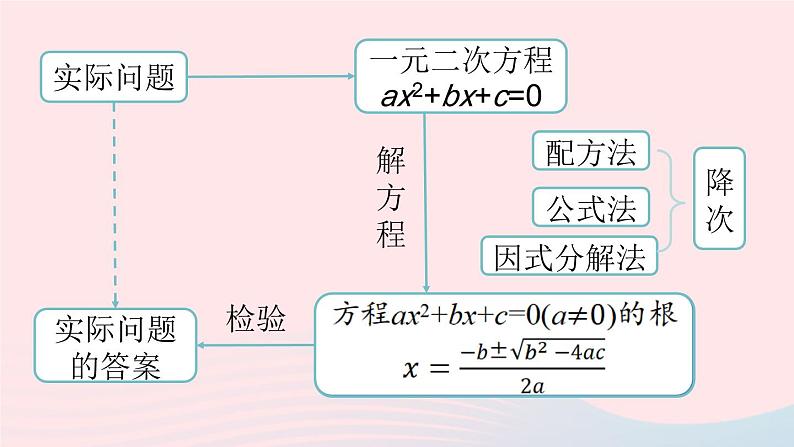
展开1.列一元二次方程解实际应用题的步骤.
检:检验所得的解是否符合题意
2.一元二次方程的实际应用.
(2)变化率问题:a(1±x)2=b
(1)疾病传播问题:(1+x)n=b
(4)双循环问题:n(n-1)
一元二次方程ax2+bx+c=0
1.某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是13,则每个支干长出( )
A.2根小分支B.3根小分支C.4根小分支D.5根小分支
解:设每个支干长出 x 个小分支.根据题意,得1+x+x·x=13,整理,得x2+x-12=0,解得x1=3,x2=-4(舍去).
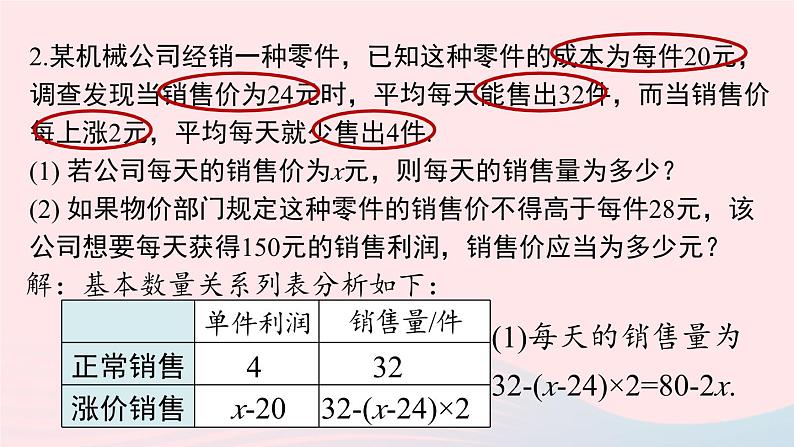
2.某机械公司经销一种零件,已知这种零件的成本为每件20元,调查发现当销售价为24元时,平均每天能售出32件,而当销售价每上涨2元,平均每天就少售出4件.(1) 若公司每天的销售价为x元,则每天的销售量为多少?(2) 如果物价部门规定这种零件的销售价不得高于每件28元,该公司想要每天获得150元的销售利润,销售价应当为多少元?
分析:销售问题的基本数量关系:
单件利润=单件的售价-单件的成本总利润=单件的利润×销售量总利润=总销售额-总成本
解:基本数量关系列表分析如下:
(1)每天的销售量为 32-(x-24)×2=80-2x.
32-(x-24)×2
解:(2)由题意可得(x-20)(80-2x)=150.解得 x1=25,x2=35.由题意知x≤28,∴x=25,即销售价应当为25元.
(2) 如果物价部门规定这种零件的销售价不得高于每件28元,该公司想要每天获得150元的销售利润,销售价应当为多少元?
3. 随着经济建设的发展,某省正加速布局以5G等为代表的战略性新兴产业. 据统计,2020年全省5G基站的数量约3.6万座. 若计划到2021年底,全省5G基站的数量是2020年的 倍;到2023年底,全省5G基站的数量将达到17.34万座. (1) 计划到2021年底,全省5G基站的数量是多少万座? (2) 按照计划,求2021年底至2023年底,全省5G基站数量的年平均增长率.
答: 计划到2021年底,全省5G基站的数量为6万座.
到2023年底,全省5G基站的数量将达到17.34万座. (2) 按照计划,求2021年底至2023年底,全省5G基站数量的年平均增长率.
解: (2) 设2021年底至2023年底,全省5G基站数量的年平均增长率为x. 列方程,得 6(1+x)2=17.34. 解方程,得 x1=0.7,x2=-2.7. 答: 2021年底至2023年底,全省5G基站数量的年平均增长率为70%.
4.为了响应市委政府提出的建设绿色家园的号召,我市某单位准备将院内一个长为30m,宽为20m的长方形空地,建成一个矩形的花园,要求在花园中修两条纵向平行和一条弯折的小道,剩余的地方种植花草,如图所示,要使种植花草的面积为532m2,那么小道的宽度应为多少米?(所有小道的进出口的宽度相等且每段小道为平行四边形)
解:设小道进出口的宽为 x m. 列方程,得 (30-2x)(20-x)=532, 整理,得x2-35x+34=0, 解得x1=1, x2=34(舍去).答:小道进出口的宽度应为1米.
1.某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮感染后就会有100台被感染.设每轮感染中平均每一台电脑会感染 x 台其他电脑,由题意列方程应为( )A.1+2x=100B.x(1+x)=100C.(1+x)2=100D.1+x+x2=100
2.有一个两位数,它的十位数字与个位数字之和是8,把十位数字和个位数字调换位置后,所得的两位数乘原来的两位数得1855,求原来的两位数.
解:设原来个位数为x,则十位数为8-x,由题意,得
[10(8-x)+x][(8-x)+10x]=1855.
整理,得x2-8x+15=0,
解得x1=3,x2=5.
经检验,x1=3,x2=5均是原方程的解,所以原来两位数为53或35.
3.(2020•上海中考)去年某商店“十一黄金周”进行促销活动期间,前六天的总营业额为450万元,第七天的营业额是前六天总营业额的12%.(1)求该商店去年“十一黄金周”这七天的总营业额;(2)去年,该商店7月份的营业额为350万元,8,9月份营业额的月增长率相同,“十一黄金周”这七天的总营业额与9月份的营业额相等.求该商店去年8,9月份营业额的月增长率.
解:(1)450+450×12%=504(万元).答:该商店去年“十一黄金周”这七天的总营业额为504万元.
(1)求该商店去年“十一黄金周”这七天的总营业额;
类似例题的素养解读见《教材帮》RJ九上21.3节中考帮
解:(2)设该商店去年8,9月份营业额的月增长率为x.依题意,得350(1+x)2=504,解得x1=0.2=20%,x2=-2.2(不合题意,舍去).答:该商店去年8,9月份营业额的月增长率为20%.
(2) 去年,该商店7月份的营业额为350万元,8,9月份营业额的月增长率相同,“十一黄金周”这七天的总营业额与9月份的营业额相等.求该商店去年8,9月份营业额的月增长率.
4.某扶贫单位为了提高贫困户的经济收入,购买了33m的铁栅栏,准备用这些铁栅栏为贫困户靠墙(墙长15m)围建一个中间带有铁栅栏的矩形养鸡场(如图所示).(1)若要建的矩形养鸡场面积为90m2,求养鸡场的长(AB)和宽(BC);(2)该扶贫单位想要建一个100m2的矩形养鸡场,这一想法能实现吗?请说明理由.
解:(1)设BC=x m,则AB=(33-3x)m.依题意,得x(33-3x)=90,解得x1=6,x2=5.当x=6时,33-3x=15,符合题意,当x=5时,33-3x=18,18>15,不合题意,舍去.答:鸡场的长(AB)为15m,宽(BC)为6m.
(1)若要建的矩形养鸡场面积为90m2,求养鸡场的长(AB)和宽(BC);
数学九年级上册21.1 一元二次方程习题课件ppt: 这是一份数学九年级上册21.1 一元二次方程习题课件ppt,共30页。
初中数学人教版九年级上册21.1 一元二次方程教学课件ppt: 这是一份初中数学人教版九年级上册21.1 一元二次方程教学课件ppt,共14页。PPT课件主要包含了直接开平方法,配方法,公式法,因式分解法,根的判别式,回顾交流,范例点击,售价进价,检测反馈,解下列方程等内容,欢迎下载使用。
初中数学第二十一章 一元二次方程综合与测试优质课件ppt: 这是一份初中数学第二十一章 一元二次方程综合与测试优质课件ppt,共21页。PPT课件主要包含了知识梳理,审审清题意,设设未知数,列列一元二次方程,解解一元二次方程,答写出答案,5几何图形问题,6商品销售问题,7数字问题,实际问题等内容,欢迎下载使用。













