





数学九年级上册第二十一章 一元二次方程综合与测试获奖ppt课件
展开1.一元二次方程的定义: 等号两边都是整式,只含有一个未知数 (一元),并且未知数的最高次数是2 (二次) 的方程叫做一元二次方程.2.一般形式:ax2 + bx +c=0 (a,b,c为常数,a≠0)3.方程的根:使方程左右两边相等的未知数的值就是这个一元二次方程的解,一元二次方程的解也叫做一元二次方程的根.
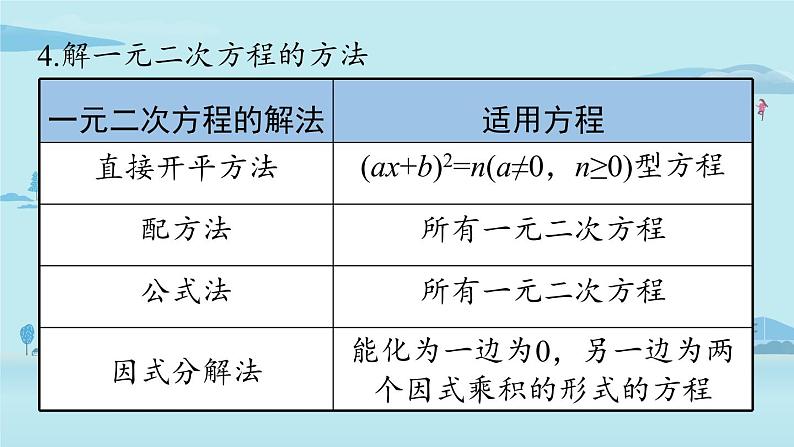
4.解一元二次方程的方法
5.一元二次方程 ax2+bx+c=0(a≠0) 的根与系数的关系
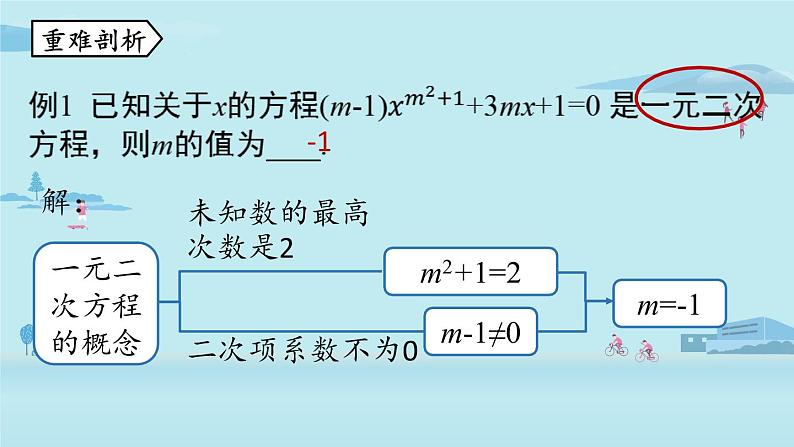
解:根据题意得,x=0是原方程的根所以m2-1=0,解得m=±1.又二次项系数不能为0,所以m≠1,即m=-1.
例2 若关于x的一元二次方程(m-1)x2+x+m2-1=0有一个根为0,则m= .
这种解题方法我们称之为“有根必代”.
例3 解下列方程 (1)x2+x-1=0 ; (2)(x-3)2=-2x(x-3) .
解:(1)a=1,b=1,c=-1
∴Δ=b2-4ac=1-4×1×(-1)=5,
根据方程的特征选择适当的方法进行解答,若多种方法都可以,则选择自己擅长的方法进行解答.
例3 解下列方程 (1)x2+x-1=0 ; (2)(x-3)2=-2x(x-3) .
解:(2)(x-3)2=-2x(x-3)
移项,得(x-3)2+2x(x-3)=0,
因式分解,得(x-3)(3x-3)=0,
∴x1=3,x2=1.
本题可以移项、因式分解,也可以化成一般式后用配方法或公式法,但是不能两边同除以(x-3).
解:解方程x2-13x+36=0得 x1=9,x2=4,即第三边长为9或4.∵9,3,6不能构成三角形,4,3,6能构成三角形,∴三角形的周长为3+4+6=13.
例4 三角形两边长分别为3和6,第三边的长是方程x2﹣13x+36=0 的根,则该三角形的周长为( )A.13 B.15 C.18 D.13或18
例5 关于x的一元二次方程 (m-1)x2-2x+1=0.(1)若方程有两个不相等的实数根,求m的取值范围;(2) 若方程的一个实数根为-1,求m的值及方程的另一个实数根.
由①得 m≠1.由②得 Δ=(-2)2-4(m-1)×1 解得 m<2.∴m<2且m≠1.
例5 关于x的一元二次方程 (m-1)x2-2x+1=0.(2) 若方程的一个实数根为-1,求m的值及方程的另一个实数根.
解:(2) 把x=-1代入原方程,得 (m-1)×(-1)2-2×(-1)+1=0. 解方程,得 m=-2. ∴原方程为 -3x2-2x+1=0.
例6 已知一元二次方程x2-4x-3=0的两根分别为m,n,则m2-mn+n2= .
解:根据根与系数的关系可知 m+n=4,mn=-3. m2-mn+n2 =m2+n2-mn =(m+n)2-3mn =42-3 ×(-3) =25.
化为含m+n与mn的形式
1.填空(1) 方程5x2-x-3=x2-3+x的二次项系数是 ,一次项系数是 ,常数项是 .
(2) 一元二次方程x2+px-2=0的一个根为2,则 p 的值为 .
一般式:4x2-2x=0
把 x=2代入方程,得 4+2p-2=0,解得 p=-1.
2.菱形ABCD的一条对角线长为6,边AB的长是方程x2-7x+12=0的一个根,则菱形ABCD的周长为( ) A. 16 B. 12 C. 16或12 D. 24
解:方程x2-7x+12=0可化为(x-3)(x-4)=0,所以x-3=0或 x-4=0,解得x1=3,x2=4,因为菱形ABCD的一条对角线长为6,所以边AB的长是4,所以菱形ABCD的周长为16.
3.用公式法和配方法分别解方程:x2-4x-1=0(要求:写出必要解题步骤).
3.用公式法和配方法分别解方程:x2-4x-1=0(要求写出必要解题步骤).
4.下列所给方程中,没有实数根的是( )A. x2+x=0 B. 5x2-4x-1=0 C.3x2-4x+1=0 D. 4x2-5x+2=0
5.关于x的一元二次方程 x2-(k+3)x+2k+2=0.(1) 求证:方程总有两个实数根;(2) 若方程有一个根小于1,求k的取值范围.
(1) 证明:Δ=[-(k+3)]2-4×1×(2k+2) =(k+3)2-8k-8 = k2-2k+1 =(k-1)2. ∵(k-1)2≥0, ∴方程总有两个实数根.
5.关于x的一元二次方程 x2-(k+3)x+2k+2=0.(2) 若方程有一个根小于1,求k的取值范围.
即 x1=k+1,x2=2.∵方程有一个根小于1,∴k+1<1,∴k<0,∴k的取值范围是k<0.
初中数学人教版九年级上册第二十五章 概率初步综合与测试完整版课件ppt: 这是一份初中数学人教版九年级上册第二十五章 概率初步综合与测试完整版课件ppt,共29页。PPT课件主要包含了直接列举法,列表法,画树状图法,用列举法求概率,用频率估计概率,知识梳理,第一枚,第二枚,跟踪训练,能力提升等内容,欢迎下载使用。
初中数学人教版九年级上册第二十五章 概率初步综合与测试优质ppt课件: 这是一份初中数学人教版九年级上册第二十五章 概率初步综合与测试优质ppt课件,共21页。PPT课件主要包含了知识梳理,随机事件,重点剖析,概率的概念,不可能发生,必然发生,概率的值,概率的取值范围,跟踪练习,能力提升等内容,欢迎下载使用。
数学第二十四章 圆综合与测试获奖课件ppt: 这是一份数学第二十四章 圆综合与测试获奖课件ppt,共46页。PPT课件主要包含了与圆有关的位置关系,直线和圆的位置关系,点和圆的位置关系,位置关系,切线的判定定理,切线的性质定理,切线长定理,知识梳理,圆内接正多边形,弧长公式等内容,欢迎下载使用。













