

- 新教材2023高中数学第六章计数原理6.2排列与组合6.2.1排列分层演练新人教A版选择性必修第三册 试卷 0 次下载
- 新教材2023高中数学第六章计数原理6.2排列与组合6.2.2排列数分层演练新人教A版选择性必修第三册 试卷 0 次下载
- 新教材2023高中数学第六章计数原理6.2排列与组合6.2.4组合数分层演练新人教A版选择性必修第三册 试卷 0 次下载
- 新教材2023高中数学第六章计数原理6.3二项式定理6.3.1二项式定理分层演练新人教A版选择性必修第三册 试卷 0 次下载
- 新教材2023高中数学第六章计数原理6.3二项式定理6.3.2二项式系数的性质分层演练新人教A版选择性必修第三册 试卷 0 次下载
人教A版 (2019)选择性必修 第三册6.2 排列与组合课后作业题
展开6.2 排列与组合 6.2.3 组合
A级 基础巩固
1.以下四个问题,属于组合问题的是( )
A.从3个不同的小球中,取出2个排成一列
B.老师在排座次时,将甲、乙两名同学安排为同桌
C.在电视节目中,主持人从100名幸运观众中选出2名幸运之星
D.从13名司机中任选出两名各开一辆车往返甲、乙两地
解析:从100名幸运观众中选出2名幸运之星,与顺序无关,是组合问题.
答案:C
2.从正方形四个顶点及其中心这5个点中,任取2个点,则这2个点的距离小于该正方形边长的线段条数为( )
A.4B.6C.8D.10
解析:如图.小于正方形边长的线段分别为OA,OB,OC,OD,共4条.
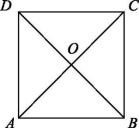
答案:A
3.A地至B地将开通高铁,共设有6个高铁站(包括A站和B站),则需设计不同票价的种类有(相同车站之间票价相同,不同车站之间票价不同)( )
A.12种B.15种 C.20种 D.30种
解析:不同的车票种类有![]() =30种,则不同的票价种类为15种.
=30种,则不同的票价种类为15种.
答案:B
4.设集合A={a1,a2,a3,a4 },则集合A中含有3个元素的子集共有
4个.
解析:从4个元素中取出3个元素组成一组就是集合A的子集,分别为{a1,a2,a3 },{a2,a3,a4 },{a1, a3,a4 },{a1,a2, a4 },共4个.
5.A,B,C,D四队女排邀请赛,通过单循环决出冠军、亚军.
(1)列出所有各场比赛的双方;
(2)列出所有冠军、亚军的可能情况.
解:(1)A—B A—C A—D B—C B—D C—D
(2)冠军、亚军的可能情况如下表.
冠军 | A | A | A | B | B | B | C | C | C | D | D | D |
亚军 | B | C | D | A | C | D | A | B | D | A | B | C |
B级 拓展提高
6.多选题下列几个问题属于组合问题的是( )
A.由1,2,3,4构成双元素集合
B.5支球队进行单循环足球比赛的分组情况
C.将全班同学按身高排队
D.由1,2,4组成无重复数字的两位数的方法
解析:由集合元素的无序性可知A属于组合问题;因为每两支球队比赛一次,没有顺序问题,故B是组合问题;按身高排队是有顺序的,故C是排列问题;D中组成的两位数与数字顺序有关,是排列问题.
答案:AB
7.古人认为,天下万物皆由金、木、水、火、土五类元素组成,如图,分别是金、木、水、火、土彼此之间存在的相生相克的关系.若从5类元素中任选2类元素,则2类元素相生的选取方案共有( )
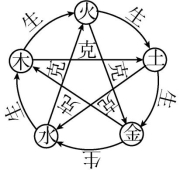
A.10种B.15种C.4种D.5种
解析:从5类元素中任选2类元素, 它们相生的选取有火土,土金,金水,水木,木火,共5种.
答案:D
8.从2,3,5,7四个数字中任取两个不同的数字相乘,有m个不同的积;任取两个不同的数字相除,有n个不同的商,则m∶n=1∶2.
解析:由题意,知不同的积有m=6个,不同的商有n=![]() =12个,
=12个,
则m∶n=1∶2.
9.某届世界杯举办期间,共32支球队参加比赛,它们先分成8个小组进行循环赛,决出16强(每队均与本组其他队赛1场,各组第一名、第二名晋级16强),这16支球队按确定的程序进行淘汰赛,每2支球队一组,每组比赛一场,即八分之一淘汰赛、四分之一淘汰赛、半决赛、决赛,最后决出冠军、亚军,此外还要决出第三名、第四名.这届世界杯总共将进行多少场比赛?
解:可分为如下几类比赛:
(1)小组循环赛,每组有6场,8个小组共有48场比赛;
(2)八分之一淘汰赛,8个小组的第一名、第二名组成16强,根据赛制规则,每2支球队一组,每组比赛1场,可以决出8强,共有8场比赛;
(3)四分之一淘汰赛,根据赛制规则,8强中每2支球队一组,每组比赛1场,可以决出4强,共有4场比赛;
(4)半决赛,根据赛制规则,4强中每2支球队一组,每组比赛1场,可以决出2强,共有2场比赛;
(5)决赛,2强比赛1场决出冠军、亚军,4强中的另2支球队比赛1场决出第三名、第四名,共有2场比赛.
综上所述,由分类加法计数原理,知总共将进行48+8+4+2+2=64场比赛.
C级 挑战创新
10.在象棋比赛中,参赛的任意两位选手都比赛一场,其中胜者得2分,负者得0分,平局各得1分.现有四名学生分别统计全部选手的总得分,统计结果为131分,132分,133分,134分,但其中只有一名学生的统计结果是正确的,则参赛选手共有( )
A.11位B.12位C.13位D.14位
解析:由题意,知“胜者得2分,负者得0分,平局各得1分”,所以每场比赛都会产生2分,那么最后总分一定为偶数,所以排除131和133,剩下132和134.假设有x位参赛选手,那么总共要进行的比赛场数为![]() ,如果132是正确的,那么x(x-1)=132,此方程的解为x=12,如果134是正确的,那么x(x-1)=134,此方程无整数解,所以共有12位参赛选手.
,如果132是正确的,那么x(x-1)=132,此方程的解为x=12,如果134是正确的,那么x(x-1)=134,此方程无整数解,所以共有12位参赛选手.
答案:B
11.甲、乙、丙等6名学生参加职业技能比赛,并根据成绩进行排名(无并列).甲、乙、丙3名学生一同去询问成绩,评委对甲说:“很遗憾,你和乙都没有得到冠军.”对乙说:“你当然不是最后两名.”对丙说:“你比甲和乙都好,但也不是冠军.”从这位评委的回答中分析,6名学生的名次情况共有( )
A.72种B.36C.96种D.48种
解析:由题意,知甲、乙、丙都不是第1名且乙不是最后两名,丙比甲和乙都好,则丙只能是第2名或第3名.当丙是第2名时,乙只能是第3名或第4名,甲只能是3至6名中除乙外的3个名次中的一个,所以有2×3×3×2×1=36种情况;当丙是第3名时,乙只能是第4名,甲只能是第5名或第6名,所以有2×3×2×1=12种情况.故共有36+12=48种不同的情况.
答案:D
人教A版 (2019)选择性必修 第三册第六章 计数原理6.2 排列与组合当堂检测题: 这是一份人教A版 (2019)选择性必修 第三册<a href="/sx/tb_c4000352_t7/?tag_id=28" target="_blank">第六章 计数原理6.2 排列与组合当堂检测题</a>,共4页。试卷主要包含了下列问题是组合问题的有等内容,欢迎下载使用。
高中数学人教A版 (2019)选择性必修 第三册6.2 排列与组合练习题: 这是一份高中数学人教A版 (2019)选择性必修 第三册6.2 排列与组合练习题,共6页。
人教A版 (2019)选择性必修 第三册6.2 排列与组合达标测试: 这是一份人教A版 (2019)选择性必修 第三册6.2 排列与组合达标测试,共5页。试卷主要包含了-=,已知=,则实数x的值为4,若-=,则n等于等内容,欢迎下载使用。













