拓展五：空间向量与立体几何大题专项训练（32道） （人教A版2019选择性必修第一册）讲义

这是一份拓展五：空间向量与立体几何大题专项训练（32道） -2023-2024学年高二数学同步精品讲义（人教A版2019选择性必修第一册），文件包含拓展五空间向量与立体几何大题专项训练32道-2023-2024学年高二数学同步精品讲义人教A版2019选择性必修第一册解析版docx、拓展五空间向量与立体几何大题专项训练32道-2023-2024学年高二数学同步精品讲义人教A版2019选择性必修第一册原卷版docx等2份试卷配套教学资源，其中试卷共92页， 欢迎下载使用。

 拓展五：空间向量与立体几何大题专项训练（32道）



类型一 异面直线所成的角（2道）
1、（2022·湖南岳阳·高二期末）如图，在直三棱柱中，侧面侧面分别为的中点，；

(1)求证：直线面；
(2)求异面直线与所成角的余弦值．







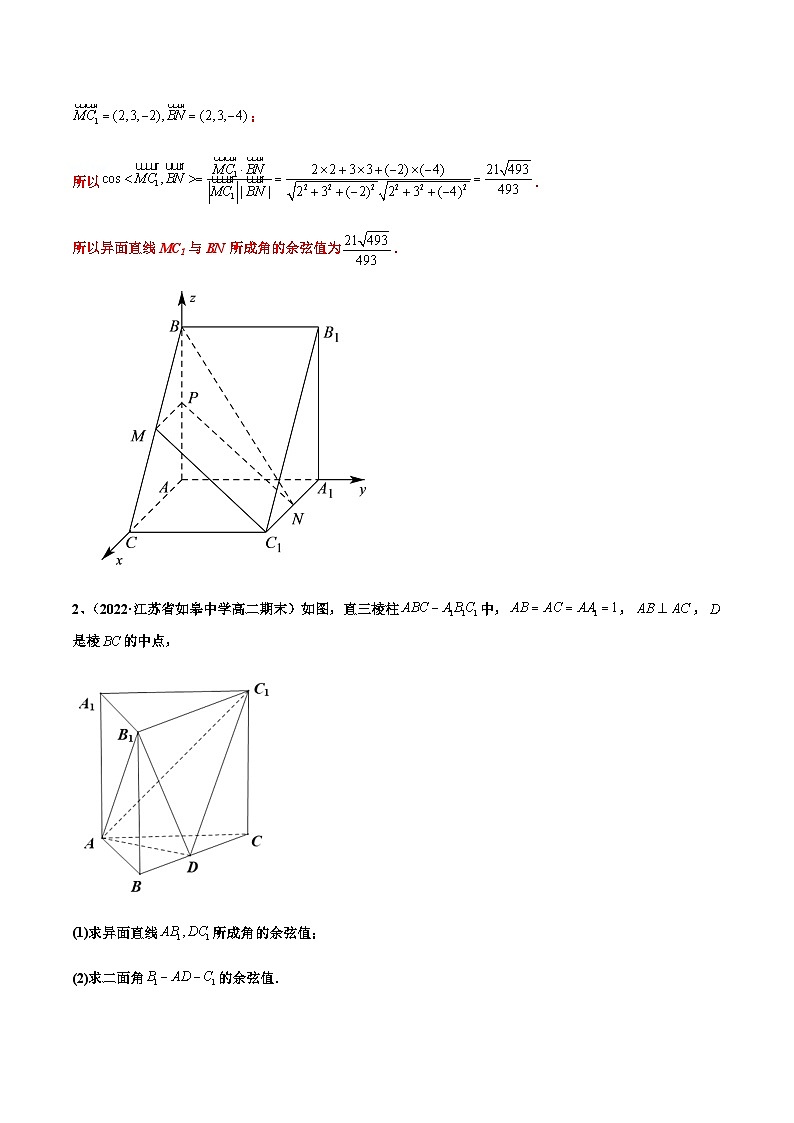
2、（2022·江苏省如皋中学高二期末）如图，直三棱柱中，，，是棱的中点，

(1)求异面直线所成角的余弦值；
(2)求二面角的余弦值．









类型二 直线与平面的夹角（5道）
3、（2022·广东·高二期末）四边形ABCD是平行四边形，，四边形ABEF是梯形，，且，，，平面平面．

(1)求证：；
(2)求直线EC与平面EFD所成角的正弦值．





4、（2022·云南玉溪·高二期末）如图，在四棱锥中，底面是矩形，，分别是，的中点．

(1)证明：平面；
(2)若是边长为的等边三角形，，平面平面，求直线与平面所成角的正弦值．
5、（2022·江苏·镇江市实验高级中学高二期末）在四棱锥中，底面ABCD为矩形，PD⊥底面ABCD，，直线PA与底面ABCD成角，点M，N分别是PA，PB的中点.

(1)求直线PA与平面PBC所成角的正弦值；
(2)求二面角的大小的余弦值.






6、（2022·江苏宿迁·高二期末）在直角梯形中，，A为线段的中点，四边形为正方形．将四边形沿折叠，使得，得到如图（2）所示的几何体．

(1)求直线与平面所成角的正弦值；
(2)当F为线段的中点时，求二面角的余弦值．

7、（2022·湖北咸宁·高二期末）如图，在梯形ABCD中，已知AB＝4，AD＝DC＝BC＝2，M为AB的中点.将沿DM翻折至，连接PC，PB．

(1)证明：DM⊥PC.
(2)若二面角P－DM－C的大小为60°，求PB与平面ABCD所成角的正弦值.




类型三 平面与平面的夹角（二面角）（12道）
8、（2022·湖北武汉·高二期末）如图，在四棱锥P−ABCD中，平面PAD⊥平面ABCD，点E为PC的中点，AB∥CD，CD⊥AD，CD＝2AB＝2，PA＝AD＝1，PA⊥AD．

(1)证明：BE⊥平面PCD；
(2)求二面角P−BD−E的余弦值．






9、（2022·广东梅州·高二期末）如图是一个四棱柱被一个平面所截的几何体，底面是正方形，是的中点，，，．

(1)证明：；
(2)求平面与平面所成二面角的余弦值．





10、（2022·江西上饶·高二期末（理））如图，在四棱锥中，底面，E､分别为棱的中点

(1)作出平面与平面BFE的交线，并说明理由.
(2)求二面角的余弦值.



11、（2022·福建·福州三中高二期末）如图，在三棱锥中，侧面为等边三角形，，，平面平面，为的中点.

(1)求证：；
(2)若，求二面角的大小.






12、（2022·四川省成都市新都一中高二期末（理））如图，点O是正方形ABCD的中心，，，，．

(1)证明：平面ABCD；
(2)若直线OE与平面ABCD所成角的正弦值为，求二面角的余弦值．

13、（2022·重庆市实验中学高二期末）已知底面ABCD为菱形的直四棱柱，被平面AEFG所截几何体如图所示.

(1)若，求证：；
(2)若，，三棱锥GACD的体积为，直线AF与底面ABCD所成角的正切值为，求锐二面角的余弦值.







14、（2022·安徽省临泉第一中学高二期末）如图，在四棱锥中，平面ABCD，M，N分别为PB，PD的中点，底面ABCD为正方形，且．

(1)若，证明：平面AMN．
(2)若平面MNA与底面ABCD所成锐二面角的大小为45°，求PC的长．



15、（2022·云南昆明·高二期末）如图，在三棱锥中，平面ABC，，，M是PA的中点.

(1)证明：；
(2)若，求平面PBC与平面BCM所成角的大小.







16、（2022·广东广州·高二期末）如图，在三棱锥中，，平面，，.

(1)求证：平面平面；
(2)若，求平面与平面的夹角大小.





17、（2022·广东广州·高二期末）如图，OP为圆锥的高，AB为底面圆O的直径，C为圆O上一点，并且，E为劣弧上的一点，且，.

(1)若E为劣弧的中点，求证：平面POE；
(2)若E为劣弧的三等分点（靠近点），求平面PEO与平面PEB的夹角的余弦值.





18、（2022·湖南郴州·高二期末）如图，直三棱柱中，是边长为的正三角形，为的中点．

（1）证明：平面；
（2）若直线与平面所成的角的正切值为，求平面与平面夹角的余弦值．






19、（2022·海南·海口中学高二期末）如图，在四棱锥中，∥,，,为边的中点，异面直线与所成的角为90°．

(1)在直线上找一点，使得直线平面PBE，并求的值；
(2)若直线CD到平面PBE的距离为，求平面PBE与平面PBC夹角的余弦值．





类型四 点到面的距离（3道）
20、（2022·江苏宿迁·高二期末）如图，三棱柱中，所有棱长都为2，且，平面平面，点P，Q分别在上，且．

(1)求证：平面；
(2)当点P是边的中点时，求点到直线的距离．


21、（2022·安徽·合肥一中高二期末）如图，在四棱锥中，底面为菱形，且，，，点为棱的中点.

（1）在棱上是否存在一点，使得平面，并说明理由；
（2）若，二面角的余弦值为时，求点到平面的距离.






22、（2022·江苏·南京师大附中高二期末）在矩形ABCD中，，点E是线段AD的中点，将△ABE沿BE折起到△PBE位置（如图），点F是线段CP的中点．

(1)求证：DF∥平面PBE：
(2)若二面角的大小为，求点A到平面PCD的距离．




类型五 空间向量动点的设法（3道）
23、（2022·江苏徐州·高二期末）如图，已知SA垂直于梯形ABCD所在的平面，矩形SADE的对角线交于点F，G为SB的中点，，.

(1)求证：平面AEG；
(2)求二面角的余弦值；
(3)在线段EG上是否存在一点H，使得BH与平面SCD所成角的大小为？若存在，求出GH的长；若不存在，说明理由.


24、（2022·江苏泰州·高二期末）如图，在正四棱锥P－ABCD中，AC，BD交于点O，，．

(1)求二面角的大小；
(2)在线段AD上是否存在一点Q，使得PQ与平面APB所成角的正弦值为？若存在，指出点Q的位置；若不存在，说明理由．
25、（2022·浙江绍兴·高二期末）如图，在四棱锥P-ABCD中，底面ABCD，，，且，，点E为棱PC的动点.

(1)当点E是棱PC的中点时，求直线BE与平面PBD所成角的正弦值；
(2)若E为棱PC上任一点，满足，求二面角P-AB-E的余弦值.




类型六 与动点有关的最值问题（4道）
26、（2022·江苏淮安·高二期末）已知四棱锥的底面为正方形，侧面PAD为等腰直角三角形，，平面平面ABCD，平面平面．

(1)求证：平面PAD；
(2)设M为l上一点，求PC与平面MAD所成角正弦值的最小值．




27、（2022·浙江·镇海中学高二期末）如图，在六面体中，是等边三角形，二面角的平面角为30°，.

(1)证明：；
(2)若点E为线段BD上一动点，求直线CE与平面所成角的正切的最大值.





28、（2022·福建省福州第八中学高二期末）已知直三棱柱中，侧面为正方形，，E，F分别为和的中点，D为棱上的点，.

(1)证明：；
(2)求当面与面所成的二面角的正弦值最小时，三棱锥的体积.



29、（2022·辽宁葫芦岛·高二期末）如图，在长方体中，底面是边长为1的正方形，侧棱长为2，且动点P在线段AC上运动．

(1)若Q为的中点，求点Q到平面的距离；
(2)设直线与平面所成角为，求的取值范围．





类型七 立体几何的探索性问题（3道）
30、（2022·广东汕尾·高二期末）如图（1）所示的四边形中，，，，，沿将进行翻折，使得，得到如图（2）所示的四棱锥.四棱锥的体积为，点为线段上的动点（与端点，不重合）.

(1)求证：平面；
(2)探求是否存在大小为的二面角.如果存在，求出此时线段的长度；若不存在，请说明理由.

31、（2022·江苏常州·高二期末）如图，在三棱柱ABC－A1B1C1中，四边形ABB1A1为正方形，四边形AA1C1C为菱形，且∠AA1C＝60°，平面AA1C1C⊥平面ABB1A1，点D为棱BB1的中点．

(1)求证：AA1⊥CD；
(2)棱B1C1（除两端点外）上是否存在点M，使得二面角B－A1M－B1的余弦值为？若存在，请指出点M的位置；若不存在，请说明理由．




32、（2022·江苏省如皋中学高二期末）如图，在四棱锥S−ABCD中，底面ABCD为矩形，，AB=2，，平面，，，E是SA的中点．

(1)求直线EF与平面SCD所成角的正弦值；
(2)在直线SC上是否存在点M，使得平面MEF平面SCD？若存在，求出点M的位置；若不存在，请说明理由．