人教A版 (2019)选择性必修 第一册3.2 双曲线学案设计

这是一份人教A版 (2019)选择性必修 第一册3.2 双曲线学案设计，共13页。学案主要包含了学习目标，自主学习，小试牛刀，经典例题，跟踪训练，当堂达标，参考答案等内容，欢迎下载使用。

【自主学习】
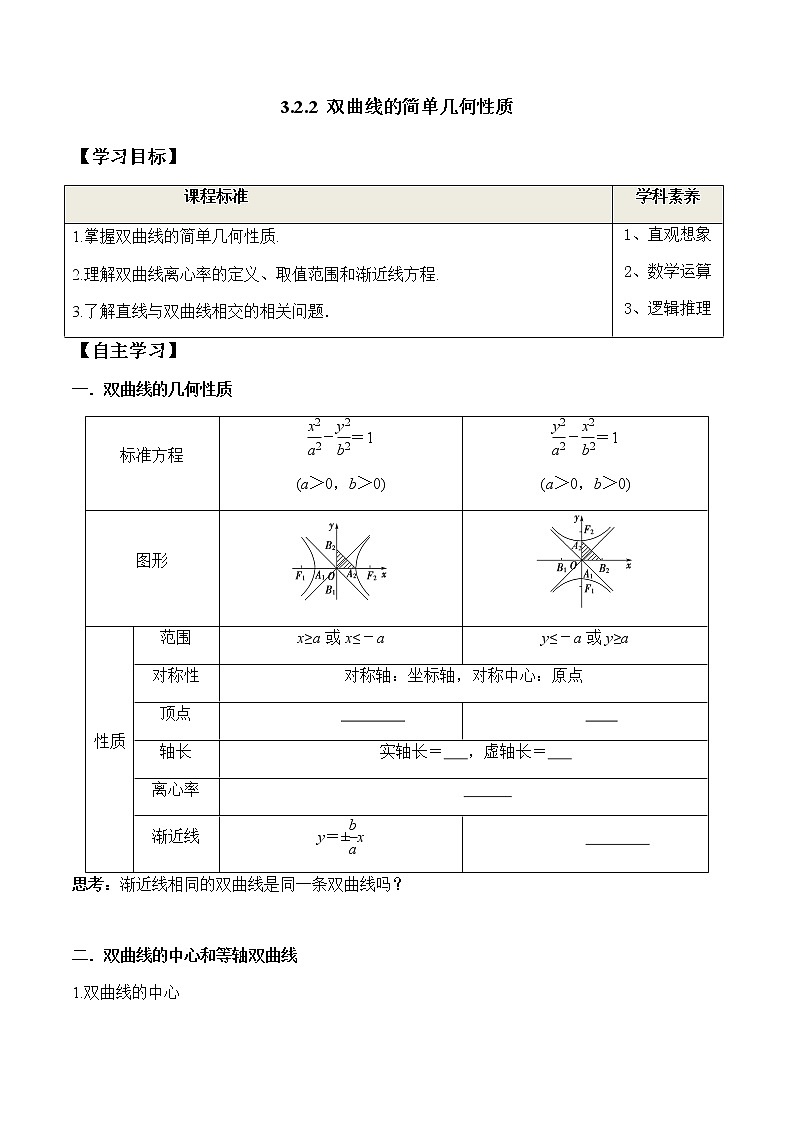
一．双曲线的几何性质
思考：渐近线相同的双曲线是同一条双曲线吗？
二．双曲线的中心和等轴双曲线
1.双曲线的中心
双曲线的 叫做双曲线的中心．
2.等轴双曲线
的双曲线叫做等轴双曲线，其离心率e＝ .
三．直线与双曲线的位置关系
将y＝kx＋m与eq \f(x2,a2)－eq \f(y2,b2)＝1联立消去y得一元方程(b2－a2k2)x2－2a2kmx－a2(m2＋b2)＝0.
【小试牛刀】
思考辨析(对的打“√”，错的打“×”)
(1)双曲线eq \f(x2,a2)－eq \f(y2,b2)＝1与eq \f(y2,a2)－eq \f(x2,b2)＝1(a>0，b>0)的形状相同．( )
(2)双曲线eq \f(x2,a2)－eq \f(y2,b2)＝1与eq \f(y2,a2)－eq \f(x2,b2)＝1(a>0，b>0)的渐近线相同．( )
(3)等轴双曲线的渐近线互相垂直，离心率e＝eq \r(2).( )
(4)椭圆的离心率与双曲线的离心率取值范围相同．( )
(5)双曲线有四个顶点，分别是双曲线与其实轴及虚轴的交点．( )
【经典例题】
题型一 根据双曲线方程研究几何性质
点拨：由双曲线的方程研究几何性质的解题步骤
(1)把双曲线方程化为标准形式；
(2)由标准方程确定焦点位置，确定a，b的值；
(3)由c2＝a2＋b2求出c值，从而写出双曲线的几何性质．
提醒：求性质时一定要注意焦点的位置．
例1 求双曲线9y2－4x2＝－36的顶点坐标、焦点坐标、实轴长、虚轴长、离心率和渐近线方程．
【跟踪训练】1 求双曲线9y2－16x2＝144的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程．
题型二 由几何性质求双曲线的标准方程
1．由几何性质求双曲线标准方程的解题思路
由双曲线的几何性质求双曲线的标准方程，一般用待定系数法．当双曲线的焦点不明确时，方程可能有两种形式，此时应注意分类讨论，为了避免讨论，也可设双曲线的方程为mx2－ny2＝1(mn＞0)．
2．常见双曲线方程的设法
(1)渐近线为y＝±eq \f(n,m)x的双曲线方程可设为eq \f(x2,m2)－eq \f(y2,n2)＝λ(λ≠0，m＞0，n＞0)；如果两条渐近线的方程为Ax±By＝0，那么双曲线的方程可设为A2x2－B2y2＝m(m≠0，A＞0，B＞0)．
(2)与双曲线eq \f(x2,a2)－eq \f(y2,b2)＝1或eq \f(y2,a2)－eq \f(x2,b2)＝1(a＞0，b＞0)共渐近线的双曲线方程可设为eq \f(x2,a2)－eq \f(y2,b2)＝λ或eq \f(y2,a2)－eq \f(x2,b2)＝λ(λ≠0)．
(3)与双曲线eq \f(x2,a2)－eq \f(y2,b2)＝1(a＞0，b＞0)离心率相等的双曲线系方程可设为eq \f(x2,a2)－eq \f(y2,b2)＝λ(λ＞0)或eq \f(y2,a2)－eq \f(x2,b2)＝λ(λ＞0)，这是因为由离心率不能确定焦点位置．
(4)与椭圆eq \f(x2,a2)＋eq \f(y2,b2)＝1(a＞b＞0)共焦点的双曲线系方程可设为eq \f(x2,a2－λ)－eq \f(y2,λ－b2)＝1(b2＜λ＜a2)．
例2 根据以下条件，求双曲线的标准方程．
(1)过点P(3，－eq \r(5))，离心率为eq \r(2)；
(2)与双曲线eq \f(x2,9)－eq \f(y2,16)＝1有共同渐近线，且过点(－3,2eq \r(3))．
【跟踪训练】2 求适合下列条件的双曲线的标准方程：
(1)虚轴长为12，离心率为eq \f(5,4)；
(2)顶点间距离为6，渐近线方程为y＝±eq \f(3,2)x.
题型三 求双曲线的离心率
点拨：求双曲线离心率的方法
(1)若可求得a，c，则直接利用e＝eq \f(c,a)得解．
(2)若已知a，b，可直接利用e＝eq \r(1＋\b\lc\(\rc\)(\a\vs4\al\c1(\f(b,a)))\s\up12(2))得解．
(3)若得到的是关于a，c的齐次方程pc2＋qac＋ra2＝0(p，q，r为常数，且p≠0)，则转化为关于e的方程pe2＋qe＋r＝0求解．
例3 已知点(2,3)在双曲线C：eq \f(x2,a2)－eq \f(y2,b2)＝1(a＞0，b＞0)上，C的焦距为4，则它的离心率为________．
【跟踪训练】3 已知双曲线的一条渐近线方程为y＝2x，则其离心率为________．
题型四 直线与双曲线的位置关系
点拨：
1.直线与双曲线位置关系的判定方法
通常把直线与双曲线的方程联立成方程组，通过消元后化为ax2＋bx＋c＝0的形式，在a≠0的情况下考查方程的判别式．
①Δ>0时，直线与双曲线有两个不同的公共点．
②Δ＝0时，直线与双曲线只有一个公共点．
③Δ<0时，直线与双曲线没有公共点．
当a＝0时，此时直线与双曲线的渐近线平行，直线与双曲线有一个公共点．
2.双曲线的弦长公式：与直线与椭圆相交所得的弦的长度求法一样．设直线y＝kx＋b与双曲线交于A(x1，y1)，B(x2，y2)，则|AB|＝eq \r(1＋k2)|x1－x2|＝eq \r(1＋k2)eq \r(x1＋x22－4x1x2)
或|AB|＝eq \r(1＋\f(1,k2))|y1－y2|＝eq \r(1＋\f(1,k2))eq \r(y1＋y22－4y1y2).
3.中点弦问题：设A(x1，y1)，B(x2，y2)是双曲线 eq \f(x2,a2) － eq \f(y2,b2) ＝1(a>0，b>0)上不同的两点，且x1≠x2，x1＋x2≠0，M(x0，y0)为线段AB的中点，则 eq \b\lc\{(\a\vs4\al\c1(\f(x eq \\al(\s\up1(2),\s\d1(1)) ,a2)－\f(y eq \\al(\s\up1(2),\s\d1(1)) ,b2)＝1，,\f(x eq \\al(\s\up1(2),\s\d1(2)) ,a2)－\f(y eq \\al(\s\up1(2),\s\d1(2)) ,b2)＝1.)) 两式相减可得 eq \f(y1－y2,x1－x2) · eq \f(y1＋y2,x1＋x2) ＝ eq \f(b2,a2) ，即kAB· eq \f(y0,x0) ＝ eq \f(b2,a2) .
例4 已知双曲线C：x2－y2＝1及直线l：y＝kx－1.
(1)若直线l与双曲线C有两个不同的交点，求实数k的取值范围；
(2)若直线l与双曲线C交于A，B两点，O是坐标原点，且△AOB的面积为eq \r(2)，求实数k的值．
【跟踪训练】4 已知双曲线焦距为4，焦点在x轴上，且过点P(2,3)．
(1)求该双曲线的标准方程；
(2)若直线m经过该双曲线的右焦点且斜率为1，求直线m被双曲线截得的弦长．
【当堂达标】
1.（多选）设中心在坐标原点，焦点在坐标轴上的双曲线的虚轴长为4，一条渐近线为，则双曲线的标准方程可以为（ ）
A．B．
C．D．
2.中心在原点，焦点在x轴上，且一个焦点在直线3x－4y＋12＝0上的等轴双曲线的方程是（ ）
A．x2－y2＝8 B．x2－y2＝4 C．y2－x2＝8 D．y2－x2＝4
3.已知双曲线eq \f(x2,a2)－eq \f(y2,b2)＝1(a＞0，b＞0)的一个焦点为F(2eq \r(5)，0)，且离心率为e＝eq \f(\r(5),2)，则双曲线的标准方程为________．
4.过双曲线x2－eq \f(y2,3)＝1的左焦点F1，作倾斜角为eq \f(π,6)的直线与双曲线交于A，B两点，则|AB|＝________.
5.若直线y＝kx与双曲线4x2－y2＝16相交，求实数k的取值范围．
6.若双曲线eq \f(x2,a2)－eq \f(y2,b2)＝1(a>0，b>0)的渐近线与圆(x－2)2＋y2＝1相切，求双曲线的离心率．
7.已知双曲线eq \f(x2,4)－y2＝1，求过点A (3，－1)且被点A平分的弦MN所在直线的方程．
【参考答案】
【自主学习】
(－a,0)，(a,0) (0，－a)，(0，a) 2a 2b e＝eq \f(c,a)>1 y＝±eq \f(a,b)x
思考：渐近线相同的双曲线有无数条，但它们实轴与虚轴的长的比值相同．
对称中心 实轴和虚轴等长 eq \r(2)
一个 两个 一个 没有
【小试牛刀】
√ × √ × ×
【经典例题】
例1 解：双曲线的方程化为标准形式是eq \f(x2,9)－eq \f(y2,4)＝1，
∴a2＝9，b2＝4，∴a＝3，b＝2，c＝eq \r(13).又双曲线的焦点在x轴上，∴顶点坐标为(－3,0)，(3,0)，
焦点坐标为(－eq \r(13)，0)，(eq \r(13)，0)，实轴长2a＝6，虚轴长2b＝4，离心率e＝eq \f(c,a)＝eq \f(\r(13),3)，渐近线方程为y＝±eq \f(2,3)x.
【跟踪训练】1 解：把方程9y2－16x2＝144化为标准方程为eq \f(y2,42)－eq \f(x2,32)＝1.
由此可知，实半轴长a＝4，虚半轴长b＝3；
c＝eq \r(a2＋b2)＝eq \r(42＋32)＝5，焦点坐标是(0，－5)，(0,5)；离心率e＝eq \f(c,a)＝eq \f(5,4)；渐近线方程为y＝±eq \f(4,3)x.
例2 解： (1)若双曲线的焦点在x轴上，设其方程为eq \f(x2,a2)－eq \f(y2,b2)＝1(a>0，b>0)，
∵e＝eq \r(2)，∴eq \f(c2,a2)＝2，即a2＝b2.①又双曲线过P(3，－eq \r(5))，∴eq \f(9,a2)－eq \f(5,b2)＝1，②
由①②得a2＝b2＝4，故双曲线方程为eq \f(x2,4)－eq \f(y2,4)＝1.
若双曲线的焦点在y轴上，设其方程为eq \f(y2,a2)－eq \f(x2,b2)＝1(a>0，b>0)，
同理有a2＝b2，③eq \f(5,a2)－eq \f(9,b2)＝1，④由③④得a2＝b2＝－4(舍去)．
综上，双曲线的标准方程为eq \f(x2,4)－eq \f(y2,4)＝1.
(2)设所求双曲线方程为eq \f(x2,9)－eq \f(y2,16)＝λ(λ≠0)，将点(－3,2eq \r(3))代入得λ＝eq \f(1,4)，
∴双曲线方程为eq \f(x2,9)－eq \f(y2,16)＝eq \f(1,4)，即双曲线的标准方程为eq \f(x2,\f(9,4))－eq \f(y2,4)＝1.
【跟踪训练】2 解：(1)设双曲线的标准方程为eq \f(x2,a2)－eq \f(y2,b2)＝1或eq \f(y2,a2)－eq \f(x2,b2)＝1(a＞0，b＞0)．
由题意知2b＝12，eq \f(c,a)＝eq \f(5,4)且c2＝a2＋b2，∴b＝6，c＝10，a＝8，
∴双曲线的标准方程为eq \f(x2,64)－eq \f(y2,36)＝1或eq \f(y2,64)－eq \f(x2,36)＝1.
(2)设以y＝±eq \f(3,2)x为渐近线的双曲线方程为eq \f(x2,4)－eq \f(y2,9)＝λ(λ≠0)，
当λ＞0时，a2＝4λ，∴2a＝2eq \r(4λ)＝6⇒λ＝eq \f(9,4).
当λ＜0时，a2＝－9λ，∴2a＝2eq \r(－9λ)＝6⇒λ＝－1.
∴双曲线的标准方程为eq \f(x2,9)－eq \f(4y2,81)＝1或eq \f(y2,9)－eq \f(x2,4)＝1.
例3 2 解析：由题意知eq \f(4,a2)－eq \f(9,b2)＝1，c2＝a2＋b2＝4，得a＝1，b＝eq \r(3)，∴e＝2.
【跟踪训练】3 eq \r(5)或eq \f(\r(5),2) 解析：当焦点在x轴上时，eq \f(b,a)＝2，这时离心率e＝eq \f(c,a)＝eq \r(1＋22)＝eq \r(5).
当焦点在y轴上时，eq \f(a,b)＝2，即eq \f(b,a)＝eq \f(1,2)，这时离心率e＝eq \f(c,a)＝eq \r(1＋\b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))\s\up12(2))＝eq \f(\r(5),2).
例4 解：(1)联立方程组eq \b\lc\{\rc\ (\a\vs4\al\c1(y＝kx－1，,x2－y2＝1，))消去y并整理得(1－k2)x2＋2kx－2＝0.
∵直线与双曲线有两个不同的交点，则eq \b\lc\{\rc\ (\a\vs4\al\c1(1－k2≠0，,Δ＝4k2＋81－k2＞0，))解得－eq \r(2)＜k＜eq \r(2)，且k≠±1.∴若l与C有两个不同交点，实数k的取值范围为(－eq \r(2)，－1)∪(－1,1)∪(1，eq \r(2))．
(2)设A(x1，y1)，B(x2，y2)，对于(1)中的方程(1－k2)x2＋2kx－2＝0，
由根与系数的关系，得x1＋x2＝－eq \f(2k,1－k2)，x1x2＝－eq \f(2,1－k2)，
∴|AB|＝eq \r(1＋k2)|x1－x2|＝eq \r(1＋k2)·eq \r(\b\lc\(\rc\)(\a\vs4\al\c1(－\f(2k,1－k2)))\s\up12(2)＋\f(8,1－k2))＝eq \r(\f(1＋k28－4k2,1－k22)).
又∵点O(0,0)到直线y＝kx－1的距离d＝eq \f(1,\r(1＋k2))，
∴S△AOB＝eq \f(1,2)·|AB|·d＝eq \f(1,2)eq \r(\f(8－4k2,1－k22))＝eq \r(2)，即2k4－3k2＝0，解得k＝0或k＝±eq \f(\r(6),2).
∴实数k的值为±eq \f(\r(6),2)或0.
【跟踪训练】4 解：(1)设双曲线方程为eq \f(x2,a2)－eq \f(y2,b2)＝1(a，b>0)，
由已知可得左、右焦点F1，F2的坐标分别为(－2,0)，(2,0)，则|PF1|－|PF2|＝2＝2a，所以a＝1，
又c＝2，所以b＝eq \r(3)，所以双曲线方程为x2－eq \f(y2,3)＝1.
（2）题意可知直线m的方程为y＝x－2，联立双曲线及直线方程消去y得2x2＋4x－7＝0，
设两交点为A(x1，y1)，B(x2，y2)，所以x1＋x2＝－2，x1x2＝－eq \f(7,2)，由弦长公式得|AB|＝eq \r(1＋k2)|x1－x2|＝eq \r(1＋k2)eq \r(x1＋x22－4x1x2)＝6.
【当堂达标】
1.AD 解析：中心在坐标原点，焦点在坐标轴上的双曲线的虚轴长为4，一条渐近线为，
可得b=2，一条渐近线为，如果双曲线的焦点坐标在x轴上，可得a=4，双曲线方程为：．如果双曲线的焦点坐标 在y轴上，可得a=1，此时双曲线方程为：．故选：AD．
2.A 解析：令y＝0，得x＝－4，∴等轴双曲线的一个焦点为(－4,0)，
∴c＝4，a2＝b2＝eq \f(1,2)c2＝eq \f(1,2)×16＝8，故选A.
3.eq \f(x2,16)－eq \f(y2,4)＝1 解析：由焦点坐标，知c＝2eq \r(5)，由e＝eq \f(c,a)＝eq \f(\r(5),2)，可得a＝4，所以b＝eq \r(c2－a2)＝2，则双曲线的标准方程为eq \f(x2,16)－eq \f(y2,4)＝1.
4. 3 解析：双曲线的左焦点为(－2,0)，设A(x1，y1)，B(x2，y2)，AB方程为y＝eq \f(\r(3),3)(x＋2)，即x－eq \r(3)y＋2＝0，由eq \b\lc\{\rc\ (\a\vs4\al\c1(x－\r(3)y＋2＝0，,x2－\f(y2,3)＝1))得8y2－12eq \r(3)y＋9＝0，则y1＋y2＝eq \f(3\r(3),2)，y1y2＝eq \f(9,8).
∴|AB|＝eq \r(\b\lc\(\rc\)(\a\vs4\al\c1(1＋\f(1,k2)))[y1＋y22－4y1y2])＝eq \r(1＋3\b\lc\[\rc\](\a\vs4\al\c1(\b\lc\(\rc\)(\a\vs4\al\c1(\f(3\r(3),2)))\s\up12(2)－4×\f(9,8))))＝3.
5. 解：易知k≠±2，将y＝kx代入4x2－y2＝16得关于x的一元二次方程(4－k2)x2－16＝0，由Δ>0可得－26.解：双曲线eq \f(x2,a2)－eq \f(y2,b2)＝1(a>0，b>0)的渐近线方程为y＝±eq \f(b,a)x，圆(x－2)2＋y2＝1的圆心为(2,0)，半径为1，则由圆心到直线的距离为1，可得eq \f(|2b|,\r(a2＋b2))＝1，解得a＝eq \r(3)b，
则c＝eq \r(a2＋b2)＝eq \r(a2＋\f(1,3)a2)＝eq \f(2\r(3),3)a，∴e＝eq \f(c,a)＝eq \f(2\r(3),3).
7.解：设M(x1，y1)，N(x2，y2)，∵M，N均在双曲线上，
∴eq \b\lc\{\rc\ (\a\vs4\al\c1(\f(x\\al(2,1),4)－y\\al(2,1)＝1，,\f(x\\al(2,2),4)－y\\al(2,2)＝1，))两式相减，得eq \f(x\\al(2,2)－x\\al(2,1),4)＝yeq \\al(2,2)－yeq \\al(2,1)，∴eq \f(y2－y1,x2－x1)＝eq \f(x2＋x1,4y2＋y1).
∵点A平分弦MN，∴x1＋x2＝6，y1＋y2＝－2.
∴kMN＝eq \f(y2－y1,x2－x1)＝eq \f(x2＋x1,4y2＋y1)＝－eq \f(3,4).
经验证，该直线MN存在．∴所求直线MN的方程为y＋1＝－eq \f(3,4)(x－3)，
即3x＋4y－5＝0.课程标准
学科素养
1.掌握双曲线的简单几何性质.
2.理解双曲线离心率的定义、取值范围和渐近线方程.
3.了解直线与双曲线相交的相关问题．
1、直观想象
2、数学运算
3、逻辑推理
标准方程
eq \f(x2,a2)－eq \f(y2,b2)＝1
(a＞0，b＞0)
eq \f(y2,a2)－eq \f(x2,b2)＝1
(a＞0，b＞0)
图形
性质
范围
x≥a或x≤－a
y≤－a或y≥a
对称性
对称轴：坐标轴，对称中心：原点
顶点


轴长
实轴长＝ ，虚轴长＝
离心率

渐近线
y＝±eq \f(b,a)x

Δ的取值
位置关系
交点个数
k＝±eq \f(b,a)时
相交
只有 交点
k≠±eq \f(b,a)且Δ＞0
有 交点
k≠±eq \f(b,a)且Δ＝0
相切
只有 交点
k≠±eq \f(b,a)且Δ＜0
相离
公共点