







初中湘教版1.1 反比例函数一等奖教学课件ppt
展开1.2.2 反比例函数?=?/?(?湘教版数学九年级上册
利用双曲线的性质解决简单的数学问题.
3
学习目标
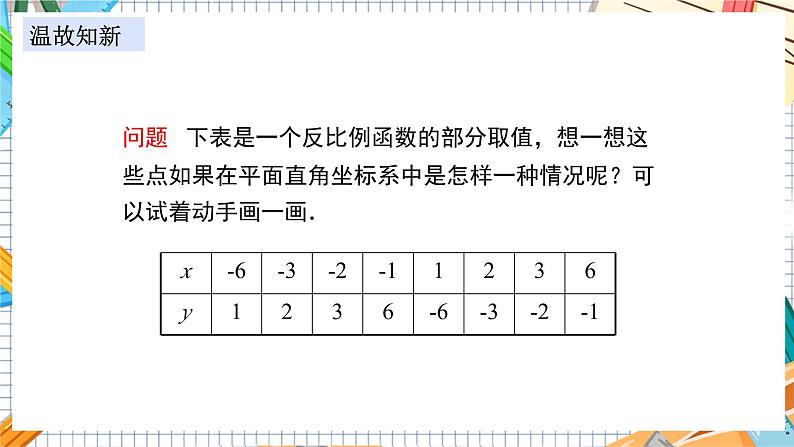
问题 下表是一个反比例函数的部分取值,想一想这些点如果在平面直角坐标系中是怎样一种情况呢?可以试着动手画一画.
温故知新
探究:画反比例函数 与 的图象.
提示:画函数的图象步骤一般分为:列表→描点→连线. 需要注意的是在反比例函数中自变量 x 不能为 0.
知识讲解
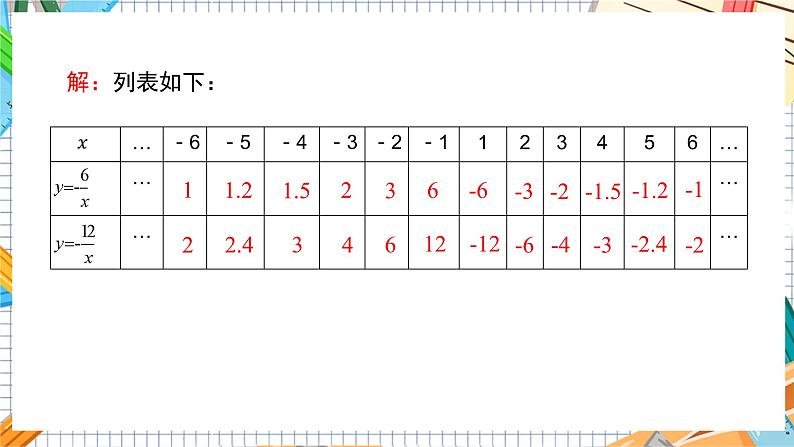
解:列表如下:
1
1.2
1.5
2
3
6
-6
-3
-2
-1.5
-1.2
-1
2
2.4
3
4
6
-6
-4
-3
-2.4
-2
12
-12
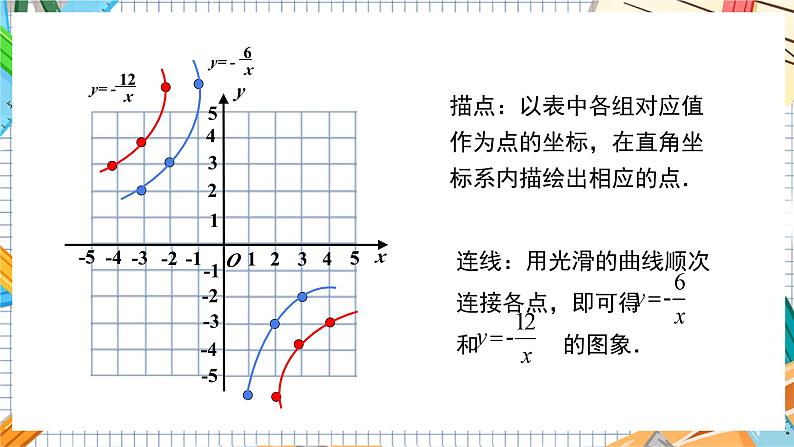
描点:以表中各组对应值作为点的坐标,在直角坐标系内描绘出相应的点.
第二、四象限
x>0时,y 随 x 的增大而增大x<0时,y 随 x 的增大而增加
x>0时,y 随 x 的增大而增大x<0时,y 随 x 的增大而增大
第二、四象限
由两条曲线组成,且分别位于第二、四象限,它们与 x 轴、y 轴都不相交;在每个象限内,y 随 x 的增大而增大.
归纳:
(1) 当 k > 0 时,双曲线的两支分别位于第一、三象限,在每一象限内,y 随 x 的增大而减小;
(2) 当 k < 0 时,双曲线的两支分别位于第二、四象限,在每一象限内,y 随 x 的增大而增大.
D
例2 如图是反比例函数 的图象,根据图像,回答下列问题:(1)k的取值范围是k>0还是k<0?说明理由;
由图可知,反比例函数的图像的两支双曲线分别位于第一三象限内,在每个象限内,函数值y随自变量x的增大而减小,因此,k>0.
(2)如果点A(-3,y1),B(-2,y2)是该函数上的两点,试比较y1、y2的大小.
因为点A(-3,y1),B(-2,y2)是该图像上的两点,且-3<0,-2<0,所以点A,B都位于第三象限.又因为-3<-2,由反比例函数图像的性质可知:y1>y2
双曲线的概念及性质
双曲线
是轴对称图形,也是以原点为对称中心的中心对称图形.
O
O
例3 如图,已知直线y=mx与双曲线 的一个交点坐标为(-1,3),则它们的另一个交点坐标是 ( )
A. (1,3) B. (3,1)C. (1,-3) D. (-1,3)
x
y
C
O
C
随堂训练
A
D
4. 下列关于反比例函数 的图象的三个结论: (1) 经过点 (-1,12) 和点 (10,-1.2); (2) 在每一个象限内,y 随 x 的增大而减小; (3) 双曲线位于二、四象限. 其中正确的是 (填序号).
(1)(3)
5.已知函数y=(m-1)xm2-5的图象是位于第二、四象限的双曲线.(1)求m的值;(2)若点(-2,y1),(-1,y2),(1,y3)都在该双曲线上,试比较y1,y2,y3的大小.
则由图象可得y2>y1>y3.
解:(1)由题意,得
解得m=-2.
(2)画出草图如图所示,
图象位于第一、三象限
图象位于第二、四象限
在每个象限内,y 随 x 的增大而减小
在每个象限内,y 随x 的增大而增大
课堂小结
湘教版九年级上册第1章 反比例函数1.1 反比例函数评优课ppt课件: 这是一份湘教版九年级上册第1章 反比例函数1.1 反比例函数评优课ppt课件,共23页。PPT课件主要包含了复习导入,方法一列表描点作图,探究新知,方法二利用对称性,图1-6,归纳小结,综上所述我们得到,巩固练习,4点Q,中考试题等内容,欢迎下载使用。
初中数学湘教版九年级上册1.1 反比例函数公开课ppt课件: 这是一份初中数学湘教版九年级上册1.1 反比例函数公开课ppt课件,共17页。PPT课件主要包含了反比例函数,反比例函数性质,反比例函数图象,探究方法,设疑导入,一般作图方法,探究新知,x≠0,图1-2,图1-4等内容,欢迎下载使用。
初中数学湘教版九年级上册1.1 反比例函数优质教学课件ppt: 这是一份初中数学湘教版九年级上册1.1 反比例函数优质教学课件ppt,文件包含教学课件九上·湘教·12反比例函数的图象与性质第1课时反比例函数yk÷xk>0的图象和性质pptx、数学九上·湘教·12反比例函数的图象与性质第1课时反比例函数yk÷xk>0的图象和性质教案docx等2份课件配套教学资源,其中PPT共15页, 欢迎下载使用。













