2023年北师大版数学八年级上册《三角形的内角和定理》课时练习（含答案）

2023年北师大版数学八年级上册

《三角形的内角和定理》课时练习

一              、选择题

1.已知△ABC的两个内角∠A＝30°，∠B＝70°，则△ABC是(　　)

A.锐角三角形       B.直角三角形       C.钝角三角形       D.等腰三角形

2.已知一个三角形三个内角度数的比是l：5：6，则其最大内角的度数为(    )

A.60°           B.75°      C.90°            D.120°

3.一个缺角的三角形ABC残片如图所示，量得∠A=60°，∠B=75°，则这个三角形残缺前的∠C的度数为（　　）

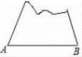
A.75°    B.60°    C.45°    D.40°

4.在△ABC中，∠A-∠B = 900，则△ABC为(　　 )三角形。
A.锐角三角形 　　B.直角三角形 　　C.钝角三角形  　　D.无法确定 

5.如图所示，BD平分∠ABC，DE∥BC，且∠D=30°，则∠AED的度数为（     ）。

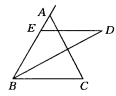
A.50°    B.60°    C.70°     D.80°

6.如图，下列说法正确的是(　　).

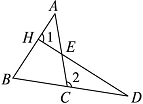
A.∠B＞∠2     B.∠2＋∠D＜180°    C.∠1＞∠B＋∠D   D.∠A＞∠1

7.下列命题是真命题的是(　　)

A.同旁内角互补

B.直角三角形的两个锐角互余

C.三角形的一个外角等于它的两个内角之和

D.三角形的一个外角大于任意一个内角

8.如图，∠ABD，∠ACD的角平分线交于点P，若∠A=50°，∠D=10°，则∠P的度数为（　　）

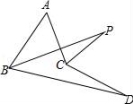
A.15°                      B.20°      C.25°        D.30°

二              、填空题

9.若一个三角形三个内角的度数之比为1：2：3，则这个三角形中的最大的角度是       ．

10.△ABC的三个外角的度数之比为2：3：4，此三角形最小的内角等于　　　　　　°．

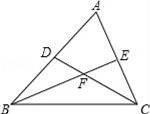
11.如图，在△ABC中，∠ABC、∠ACB的平分线BE、CD相交于点F，∠ABC=42°，∠A=60°，则∠BFC=_______．

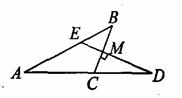
12.如图，BC⊥ED于点M，∠A=27°，∠D=20°，则∠ABC=      ．

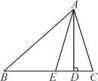
13.如图，在△ABC中，AD是BC边上的高，点E在线段BD上，且AE平分∠BAC，若∠B＝40°，∠C＝78°，则∠EAD＝         .

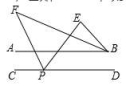
14.如图，AB∥CD，点P为CD上一点，∠EBA、∠EPC的角平分线于点F，已知∠F=40°，则∠E=　   　度.

三              、解答题

15.如图，已知∠A=20°，∠B=27°，AC⊥DE，求∠1，∠D的度数．

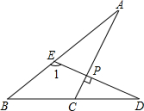
16.已知在△ABC中，∠A：∠B：∠C=2：3：4，CD是∠ACB平分线，求∠A和∠CDB的度数.

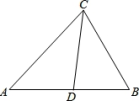
17.如图,∠ABC=38°,∠ACB=100°,AD平分∠BAC,AE是BC边上的高,求∠DAE的度数.

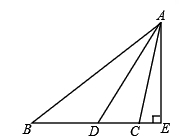
18.如图，在△ABC中，∠ACB=90°，AE是角平分线，CD是高，AE，CD相交于点F.

试说明：∠CEF=∠CFE.

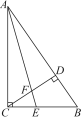
19.如图,CD是△ABC中∠ACB的外角平分线, 请猜测∠BAC和∠B的大小关系,并说明理由.

20.△ABC 中，AD、BE、CF是角平分线，交点是点 G，GH⊥BC。求证：∠BGD=∠CGH.

答案

1.A.

2.C

3.C

4.C　

5.B

6.B

7.B.

8.B.

9.答案为：90°．

10.答案为：20．

11.答案为：120°．

12.答案为：43°； 

13.答案为：19 °

14.答案为：80.

15.解：∵AC⊥DE∴∠APE=90°

∵∠1=∠A+∠APE,∠A=20°∴∠1=110°

∵∠1+∠B+∠D=180°, ∠B=27°         ∴∠D=43°

16.解：∵在△ABC中，∠A：∠B：∠C=2：3：4，∠A+∠ACB+∠B=180°，

∴∠A=×180°=40°，∠ACB=×180°=80° 

∵CD是∠ACB平分线，∴∠ACD=0.5∠ACB=40°

∴∠CDB=∠A+∠ACD=40°+40°=80°

17.

18.解：因为∠ACB=90°，CD是高，

所以∠ACD＋∠CAB=90°，∠B＋∠CAB=90°，

所以∠ACD=∠B.

因为AE是角平分线，

所以∠CAE=∠BAE.

因为∠CEF=∠BAE＋∠B，∠CFE=∠CAE＋∠ACD，

所以∠CEF=∠CFE.

19.解：∠BAC＞∠B，理由如下：

∵CD是△ABC中∠ACB的外角平分线，

∴∠ACD=∠ECD.

∵∠BAC是△ACD的外角,

∴∠BAC＞∠ACD

∴∠BAC＞∠ECD.

又∵∠ECD是△BCD的外角,

∴∠ECD＞∠B.

∴∠BAC＞∠B.

20.证明：根据题意可知，AD平分∠BAC，BE平分∠ABC，CF平分∠BCA，

∵∠BGD是△AGB的外角，

∴∠BGD = ∠GAB＋∠GBA =∠BAC＋∠ABC =(∠BAC＋∠ABC)

=(180°－∠ACB) = 90°－∠ACB = 90°－∠BCF，

∵GH⊥BC，

∴∠CHG = 90°，

∴∠CGH = 90°－∠HCG = 90°－∠BCF，

∴∠BGD = ∠CGH.