初中人教版18.2.2 菱形教案
展开菱形的判定
一、教学目标
(一)知识与技能:经历菱形的判定方法的探究过程,掌握菱形的三种判定方法.
(二)过程与方法:经历利用菱形的定义探究菱形其它判定方法的过程,培养学生动手实验、观察、推理的意识,发展学生的逻辑思维能力和演绎能力.
(三)情感态度与价值观:在探究菱形判定方法的活动中获得成功的体验,通过运用菱形的判定和性质,锻炼克服困难的意志,建立自信心.
二、教学重点、难点
重点:菱形的判定定理的探究.
难点:菱形的性质与判定的综合应用.
 三、教学过程
三、教学过程
忆一忆
1.菱形的定义:有一组邻边相等的平行四边形叫做菱形.
2.菱形的性质:菱形的四条边都相等;菱形的两条对角
线互相垂直,并且每一条对角线平分一组对角.
探究
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可转动的十字架,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形呢?

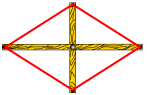
猜想:对角线互相垂直的平行四边形是菱形.
求证:对角线互相垂直的平行四边形是菱形.
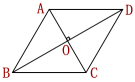 已知:如图,在□ABCD中,对角线AC、BD相交于O点,且BD⊥AC.
已知:如图,在□ABCD中,对角线AC、BD相交于O点,且BD⊥AC.
求证:□ABCD是菱形.
证明:∵ 四边形ABCD是平行四边形
∴ AO=CO
∵ BD⊥AC
∴ AB=BC (线段垂直平分线上的点到这条线段两个端点的距离相等)
∴ □ABCD是菱形
思考
我们知道,菱形的四条边相等. 反过来,四条边相等的四边形是菱形吗?
 求证:四条边相等四边形是菱形.
求证:四条边相等四边形是菱形.
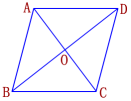
已知:如图,四边形ABCD,AB=BC=CD=AD.
求证:四边形ABCD是菱形.
证明:∵ AB=CD,BC=AD
∴ 四边形ABCD是平行四边形
又∵ AB=BC
∴ 四边形ABCD是菱形
菱形的判定定理1:对角线互相垂直的平行四边形是菱形.
菱形的判定定理2:四条边相等四边形是菱形.
定理1几何符号语言:
 ∵ 四边形ABCD是平行四边形,且AC⊥BD
∵ 四边形ABCD是平行四边形,且AC⊥BD
∴ 四边形ABCD是菱形
定理2几何符号语言:
∵ AB=BC=CD=AD
∴ 四边形ABCD是菱形
例4如图,□ABCD的对角线AC、BD交于点O,且AB=5,AO=4,BO=3.求证:□ABCD是菱形.
证明:∵ AB=5,AO=4,BO=3
∴ AB2=AO2+BO2 ∴ △OAB是直角三角形
∴ △OAB是直角三角形
∴ AC⊥BD
∴ □ABCD是菱形
练习
2.一个平行四边形的一条边长是9,两条对角线的长分别是12和![]() ,这是一个特殊的平行四边形吗?为什么?求出它的面积.
,这是一个特殊的平行四边形吗?为什么?求出它的面积.
 解:四边形ABCD是菱形.理由如下:
解:四边形ABCD是菱形.理由如下:
∵ 四边形ABCD是平形四边形,AB=9,AC=12,BD=![]()
∴ AO=![]() AC=6,BO=
AC=6,BO=![]() BD=
BD=![]()
∵ 62+(![]() )2=92
)2=92
即 AO2+BO2=AB2
∴ AC⊥BD
∴ 四边形ABCD是菱形
∴ S菱形ABCD=![]() ×12×
×12×![]() =
=![]()
3.如图,两张等宽的纸条交叉叠放在一起,重合的四边形ABCD是一个菱形吗?为什么?
 解:四边形ABCD是菱形.理由如下:
解:四边形ABCD是菱形.理由如下:
∵ AB∥CD,AD∥BC
∴ 四边形ABCD是平行四边形过点A分别作BC,CD边上
的高AE,AF,则AE=AF.
∵ S□ABCD=BC×AE=CD×AF
∴ BC=CD
∴ 四边形ABCD是菱形
课堂小结
1.本节课你有哪些收获?2.还有没解决的问题吗?
四、教学反思
在运用判定时,要遵循先易后难的原则,让学生先会运用判定解决简单的证明题,再由浅入深,学会灵活运用. 通过做不同形式的练习题,让学生能准确掌握菱形的判定并会灵活运用.
数学2.6.2菱形的判定教案: 这是一份数学<a href="/sx/tb_c95357_t8/?tag_id=27" target="_blank">2.6.2菱形的判定教案</a>,共4页。教案主要包含了知识与技能,过程与方法,情感态度,教学重点,教学难点,教学说明等内容,欢迎下载使用。
初中数学北师大版九年级上册1 菱形的性质与判定教案: 这是一份初中数学北师大版九年级上册1 菱形的性质与判定教案,共8页。教案主要包含了当堂训练,定义法,对角线互相垂直,四条边相等等内容,欢迎下载使用。
初中数学2. 菱形的判定教案及反思: 这是一份初中数学2. 菱形的判定教案及反思,共9页。