高中数学人教A版 (2019)必修 第一册第一章 集合与常用逻辑用语1.3 集合的基本运算示范课ppt课件

这是一份高中数学人教A版 (2019)必修 第一册第一章 集合与常用逻辑用语1.3 集合的基本运算示范课ppt课件，共24页。PPT课件主要包含了PART1并集，Venn图，A∪B，PART2交集，A∩B，PART3补集，能力提升等内容，欢迎下载使用。

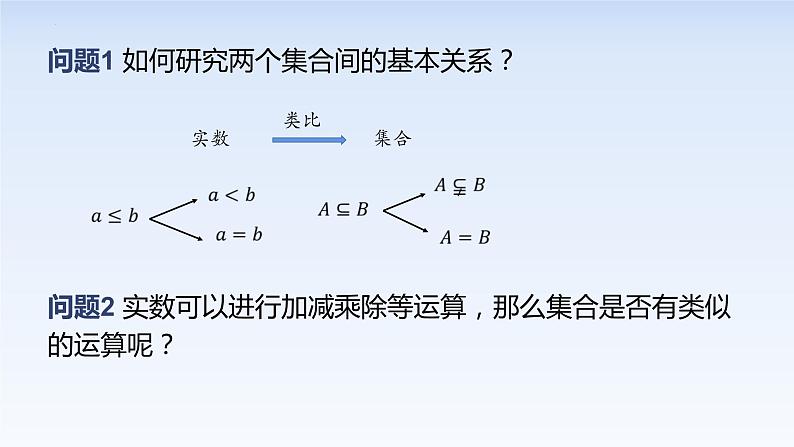
问题1 如何研究两个集合间的基本关系？
问题2 实数可以进行加减乘除等运算，那么集合是否有类似的运算呢？
学校食堂1号的菜品集合记为A={清炒白菜，炒豆芽，家常豆腐，油闷大虾，炸鸡腿，红烧鸡块}，2号的菜品集合记为B={清炒白菜，苦瓜炒蛋，红烧茄子，土豆牛腩，玉米排骨，辣子鸡丁}。
问题3 这两天吃过的所有菜品记为集合C，那么集合C等于什么？问题4 这两天吃过的相同的菜品集为集合D，那么集合D等于什么？
1.定义：由所有属于集合A或B的元素组成的集合，称为集合A与集合B的并集，记作A∪B，读作“A并B”，即A∪B＝{x|x∈A或x∈B}.
(1)A∪B＝B∪A (2)A∪A＝A (3)A∪＝A(4)
1. 设A＝{4，5，6，8}，B＝{3，5，7，8}，求A∪B.
解：A∪B＝{3，4，5，6，7，8}
!!!在求并集时，两个集合中相同的元素只列举一次!!!
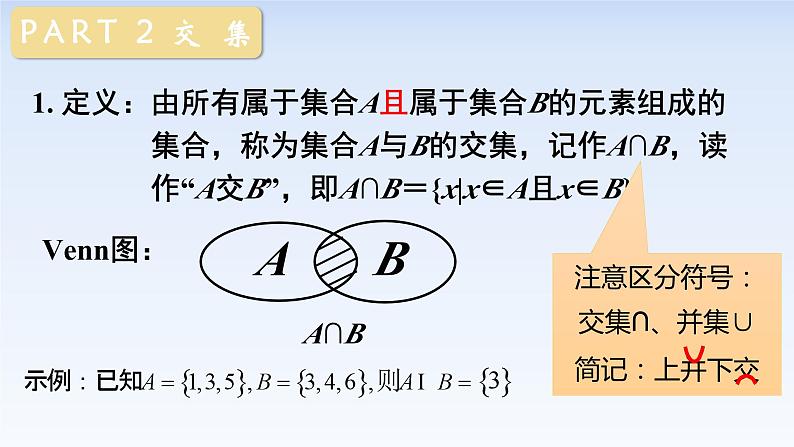
1. 定义：由所有属于集合A且属于集合B的元素组成的集合，称为集合A与B的交集，记作A∩B，读作“A交B”，即A∩B＝{x|x∈A且x∈B}.
注意区分符号：交集∩、并集∪简记：上并下交
(1)A∩B＝B∩A(2)A∩A＝A(3)A∩＝(4)
1. 全集：如果一个集合含有所研究问题中涉及的所有元素， 那么就称这个集合为全集，通常记作U.
2. 补集：由全集U中不属于集合A的所有元素组成的集合称为集合A相对于全集U的补集，简称为集合A的补集，记作CUA，即CUA＝{x|x∈U且xA}.
①A∪(CUA)=U②A∩(CUA)=③CU(CUA)=A
设U={x|x是小于9的正整数}，A={1，2，3}，B={3，4，5，6}，求CUA，CUB.
解：U={1，2，3，4，5，6，7，8} CUA={4，5，6，7，8} CUB={1，2，7，8}
例1 集合的并集、交集与补集运算
(1)已知集合A={x|x2-4x+3=0},集合B={x|(x-3)(x+1)=0},求A∩B,A∪B.
(3)若集合A={x|-1≤x<1},当S分别取下列集合时,求∁SA. ①S=R; ②S={x|x≤2}; ③S={x|-4≤x≤1}.
解 (1)∵集合A={x|x2-4x+3=0},∴A={1,3}.∵集合B={x|(x-3)(x+1)=0},∴B={-1,3}.∴A∩B={3},A∪B={-1,1,3}.
解（3） ①把集合S和A表示在数轴上,如图所示,由图知∁SA={x|x<-1,或x≥1}.②把集合S和A表示在数轴上,如图所示,由图知∁SA={x|x<-1,或1≤x≤2}.③把集合S和A表示在数轴上,如图所示,由图知∁SA={x|-4≤x<-1,或x=1}.
练习巩固 集合的并集、交集与补集运算
设集合M={m∈Z|-3答案 B　由题得,M={m∈Z|-3例2 已知集合的交集、并集求参数的值或取值范围
(1)已知a∈R,集合A={-4,2a-1,a2},B={a-5,1-a,9},若9∈A∩B,则实数a的值为　　　　　. 
答案 5或-3解析 ∵9∈A∩B,∴9∈A且9∈B,∴2a-1=9或a2=9,解得a=5或a=±3.当a=5时,A={-4,9,25},B={0,-4,9},符合题意;当a=3时,A={-4,5,9},B不满足集合中元素的互异性,故a≠3;当a=-3时,A={-4,-7,9},B={-8,4,9},符合题意.综上可得a的值为5或-3.
(2)集合A={x|-1解 ①A={x|-1例3 集合的交集、并集性质的应用
设集合M={x|-2例4 集合的补集性质的应用
已知全集为R,集合A={x|x答案 {a|a≥2}解析 ∵B={x|1已知集合A={x|0≤x≤2},B={x|a≤x≤a+3}.(1)若(∁RA)∪B≠R,求a的取值范围;(2)若A∩B≠A,求a的取值范围.
解 (1)∵A={x|0≤x≤2},∴∁RA={x|x<0,或x>2}.设(∁RA)∪B=R,如图所示.∴a≤0,且a+3≥2,即a≤0,且a≥-1,∴满足(∁RA)∪B≠R的实数a的取值范围是{a|a<-1,或a>0}.(2)若A∩B=A,则A⊆B,又A≠⌀,∴当A∩B≠A时,a的取值范围为集合{a|-1≤a≤0}的补集,即{a|a<-1,或a>0}.