2023年湖北省武汉市东湖高新区中考五月调考数学试题（无答案）

2023年湖北省武汉市东湖高新区中考五月调考数学试题

学校:___________姓名：___________班级：___________考号：___________

一、单选题

1．的相反数是（    ）

A．2 B． C． D．

二、未知

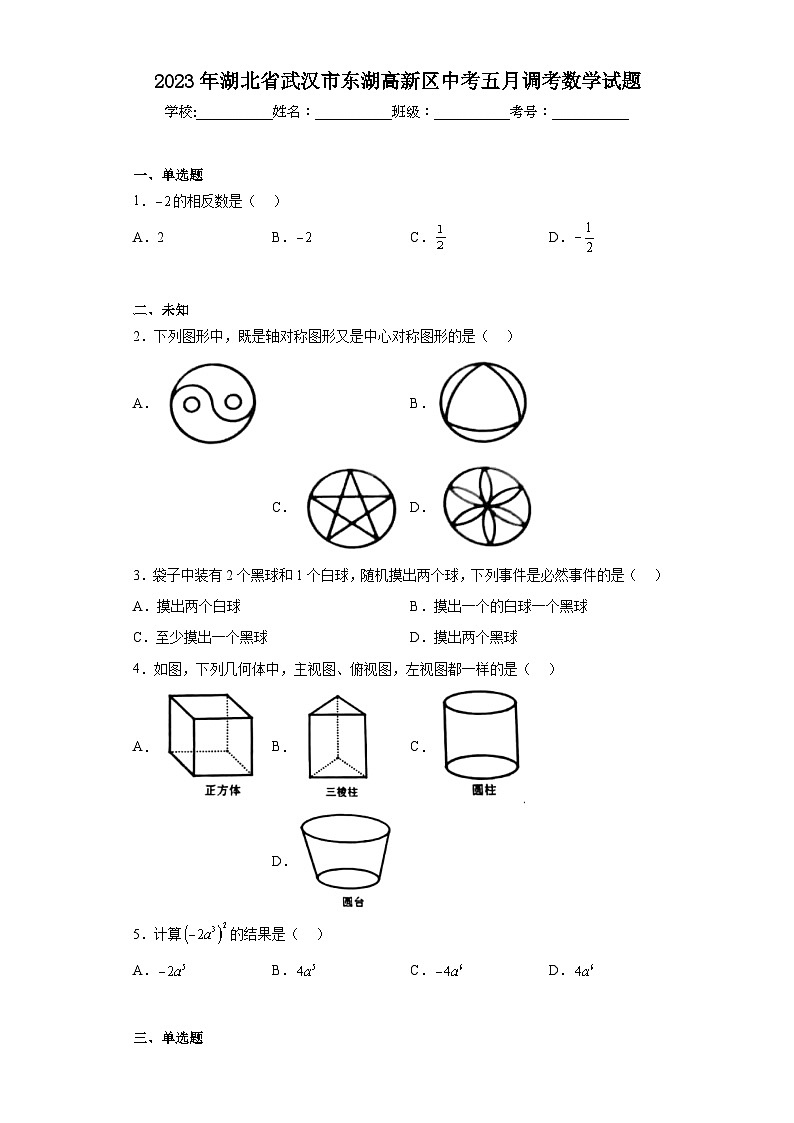
2．下列图形中，既是轴对称图形又是中心对称图形的是（    ）

A． B． C． D．

3．袋子中装有2个黑球和1个白球，随机摸出两个球，下列事件是必然事件的是（    ）

A．摸出两个白球 B．摸出一个的白球一个黑球

C．至少摸出一个黑球 D．摸出两个黑球

4．如图，下列几何体中，主视图、俯视图，左视图都一样的是（    ）

A． B． C． D．

5．计算的结果是（    ）

A． B． C． D．

三、单选题

6．若点，，在反比例函数的图象上，则a，b，c的大小关系是（    ）

A． B． C． D．

四、未知

7．已知，是一元二次方程的两根，则的值是（    ）

A． B．2 C． D．

8．如图，甲从村匀速骑自行车到村，乙从村匀速骑摩托车到村，两人同时出发，到达目的地后立即停止运动，甲、乙两人离村的距离）与他们骑车的时间之间的函数关系如图所示，则下列说法错误的是（    ）

A．、两村的距离为 B．甲的速度为

C．乙的速度为 D．乙运动到达目的地

9．17~18世纪，中国数学家、天文学家梅文鼎和英国数学家辛普森各自独立地用简化了的“同径法”证明了正弦定理：“三角形中每一边和它所对角的正弦值的比都等于外接圆的直径”；已知中，，，，则的外接圆直径为（    ）

A． B． C． D．

10．为坐标平面内一点，且，，过点作直线与平行，交轴．当点在区域内运动时，求的最大值为（    ）

A．3 B．2 C．1 D．4

五、填空题

11．写出一个比4小的正无理数：__________．

六、未知

12．第十四届全国人民代表大会政府工作报告指出：过去一年，我国脱贫人口务工规模超过3200万人，3200用科学记数法表示是__________．

13．有两把不同的锁和三把钥匙，其中两把钥匙恰好分别能打开这两把锁，第三把钥匙不能打开这两把锁．任意取出一把钥匙去开任意的一把锁，一次打开锁的概率是__________．

14．如图，建筑物的高度为，从建筑物的楼顶测得点的俯角为，测得点的俯角为，则建筑物的高度是__________（已知，结果用“四舍五入”法保留小数点后一位）．

15．已知函数（，是常数，且），过．下列结论中：

①其图象关于直线对称；

②关于的不等式的解集为；

③若点，在函数图象上，，且，则；

④函数与平行于轴的直线有且只有3个交点．

其中正确的是__________（塤写序号）．

16．如图，矩形中，，为上一点，，作交延长线于，为中点，，则的长为__________．

17．解不等式组：请结合题意填空，完成本题的解答．

(1)解不等式①，得__________；

(2)解不等式②，得__________ ；

(3)把不等式①和②的解集在数轴上表示出来；

(4)原不等式组的解集为__________．

18．如图，中，，平分，

(1)求证：；

(2)若，直接写出的值．

19．某校开学初对七年级学生进行一次安全知识问答测试，设成绩为分（为整数），将成绩评定为优秀、良好、合格、不合格四个等级（优秀、良好、合格、不合格分别用A、B、C、D表示），A等级：，B等级：，C等级：，D等级：．该校随机抽取了一部分学生的成绩进行调查，并绘制成如图不完整的统计图表．

请你根据统计图表提供的信息解答下列问题：

(1)上表中的__________，__________，__________；

(2)这组数据的中位数所在的等级是__________；

(3)该校决定对分数低于80分的学生进行安全再教育，已知该校七年级共有1000名学生，求该校七年级需要进行安全再教育的学生有多少人？

20．如图，是的直径，为延长线上一点，切于，是的中点，交于，

(1)求证：；

(2)若，，求的长．

21．如图，是由小正方形组成的网格，每个小正方形的顶点叫做格点．、、三点是格点，点在上，在上，仅用无刻度的直尺在给定网格中完成画图．

(1)在图1中，以为边画菱形；再将点绕点旋转一个角度，使其对应点落在上，画出点；

(2)在图2中，在上画点，使最小；再画线段，使．

22．如图1，为地面，、为一个小山坡，它的高度为10米，坡比为，在坡顶有一个自动浇灌装置（其高度忽略不计），它喷出的水柱呈抛物线形状，现只考虑右侧山坡，建立如图2所示的平面直角坐标系，已知水柱在与的水平距离为6米处达到最高，且距地面的最高距离为13米，

(1)求抛物线的解析式；

(2)求水柱浇灌的最远点离地面的高度；

(3)如果给浇灌装置安装一个支架，则可以使水柱覆盖整个山坡，问浇灌装置还要升高多少米，才能使水柱覆盖整个山坡？

23．探索发现：如图1，等边中，为中点，、分别是、上的两点，．

(1)求证：；

(2)为上一点，若，求的值；

迁移拓展：

(3)如图2，等腰中，为斜边的中点，为中克，．是上的点，，为上一点，若，直接写出的长．

24．已知抛物线与轴交于、两点，与轴交于点，，且的面积为6

(1)求抛物线的对称轴和解析式；

(2)如图1，若，为抛物线上两点，以、、、为顶点的四边形是平行四边形，设点横坐标为，求的值；

(3)如图2，过定点的直线交抛物线于，两点，过点的直线与抛物线交于点，求证：直线必过定点．