2023年湖北省武汉市蔡甸区九年级五月调考数学试卷（含解析）

2023年湖北省武汉市蔡甸区九年级五月调考数学试卷

一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）

1.  的相反数是(    )

A.  B.  C.  D.

2.  下列图形是我国国产品牌汽车的标识，在这些汽车标识中，是中心对称图形的是(    )

A.  B.  C.  D.

3.  有五张背面完全相同的卡片，正面分别标有数字、、、、，从中同时抽取两张，则下列事件为随机事件的是(    )

A. 两张卡片的数字之和等于 B. 两张卡片的数字之和等于
C. 两张卡片的数字之和大于或等于 D. 两张卡片的数字之和等于

4.  如图是由个大小相同的正方体组合而成的几何体，其左视图是(    )

A.
B.
C.
D.

5.  计算的结果是(    )

A.  B.  C.  D.

6.  若点，，在反比例函数是常数的图象上，则，，的大小关系是(    )

A.  B.  C.  D.

7.  已知，是一元二次方程的两根，则的值为(    )

A.  B.  C.  D.

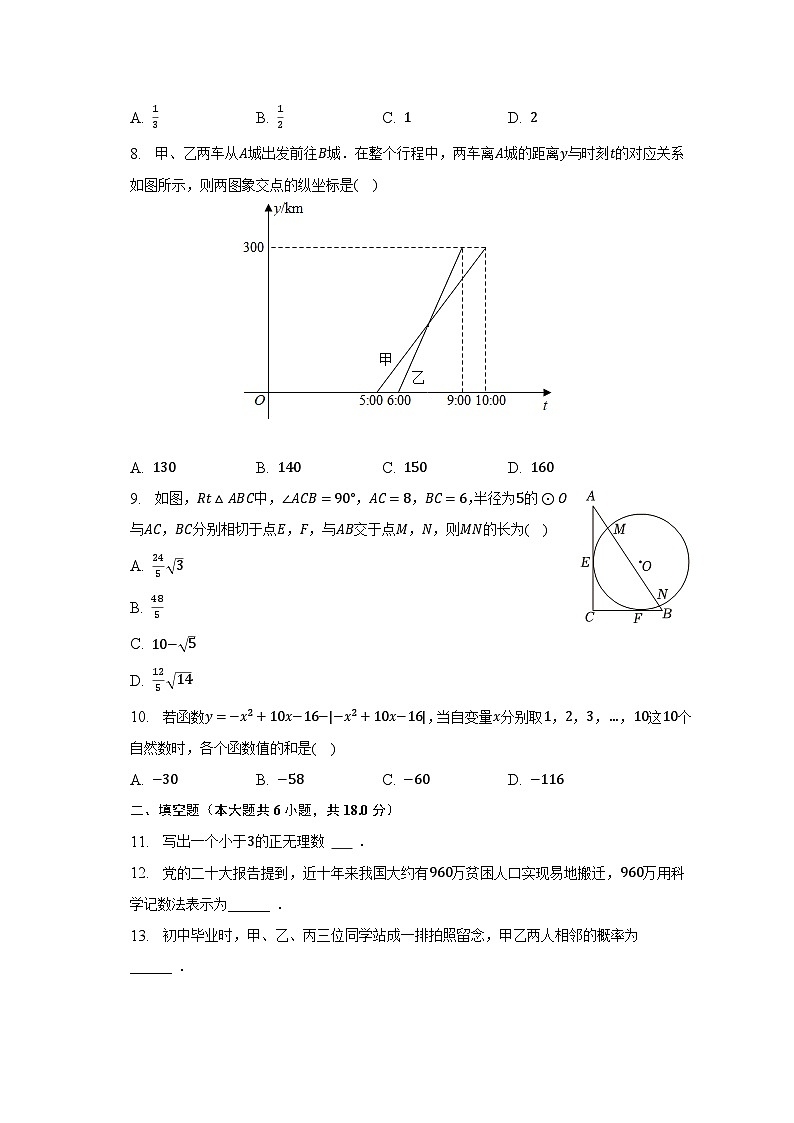
8.  甲、乙两车从城出发前往城．在整个行程中，两车离城的距离与时刻的对应关系如图所示，则两图象交点的纵坐标是(    )

A.  B.  C.  D.

9.  如图，中，，，，半径为的与，分别相切于点，，与交于点，，则的长为(    )

A.
B.
C.
D.

10.  若函数，当自变量分别取，，，，这个自然数时，各个函数值的和是(    )

A.  B.  C.  D.

二、填空题（本大题共6小题，共18.0分）

11.  写出一个小于的正无理数        ．

12.  党的二十大报告提到，近十年来我国大约有万贫困人口实现易地搬迁，万用科学记数法表示为______ ．

13.  初中毕业时，甲、乙、丙三位同学站成一排拍照留念，甲乙两人相邻的概率为______ ．

14.  某数学兴趣小组开展了“笔记本电脑的张角大小、顶部边缘离桌面的高度与用眼舒适度关系”的实践探究活动如图，当张角时，顶部边缘处离桌面的高度的长为，此时用眼舒适度不太理想，小组成员调整张角大小继续探究，最后联系黄金比知识，发现当张角时点是的对应点，用眼舒适度较为理想，此时顶部边缘处离桌面的高度的长为______ 结果精确到：参考数据：，，

 

15.  二次函数的大致图象如图所示，顶点坐标为，下列结论：；；若方程有两个根，，且，则；若抛物线与轴的交点在与之间，则的取值范围是其中正确结论的是______ ．

16.  如图，是矩形边上一点，若，，，则的值是______．

三、解答题（本大题共8小题，共72.0分。解答应写出文字说明，证明过程或演算步骤）

17.  本小题分
解不等式组，请按下列步骤完成解答．

解不等式，得______ ；
解不等式，得______ ；
把不等式和的解集在数轴上表示出来；
原不等式组的解集是______ ．

18.  本小题分
如图，，，是边上的点，，．
求证：；
若，写出直接的值．

19.  本小题分
某中学开展了“手机伴我健康行”主题活动他们随机抽取部分学生进行“使用手机的目的”和“每周使用手机的时间”的问卷调查，将收集的数据整理后，绘制成了两幅不完整的统计图已知“查资料”的人数是人．

本次调查的样本容量是______ ，在扇形统计图中，“玩游戏”对应的圆心角度数是______ 度，条形统计图中“每周使用手机的时间小时以上”的人数是______ ；
该校有学生人，估计每周使用手机时间在小时以上不含小时的人数．

20.  本小题分
如图，是的直径，是弦，是的中点，与交于点是延长线上的一点，且．
求证：为的切线；
连接，取的中点，连接若，，求的长．

 

21.  本小题分
如图，在由小正方形组成的的网格中，每个小正方形的顶点叫做格点，的三个顶点都是格点，仅用无刻度直尺在网格中作图，作图过程用虚线，作图结果用实线表示．
如图中，在上找点，使，过点作，垂足为；
如图，是网格中的格点，在线段上找一点，使得点到的距离等于的长；在上找点，连接，使得．

 

22.  本小题分
如图，学校计划建造一块边长为的正方形花坛，分别取四边的中点，，，构成四边形，四边形部分种植甲种花，在正方形四个角落构造个全等的矩形区域种植乙种花，剩余部分种草坪设小矩形的边长为，面积为，已知种植甲种花元，乙种花元，草坪元，种植总费用为元．
直接写出关于的函数关系式以及与的函数解析式；
当种植总费用为元时，求的值；
为了花坛的美观，设计小矩形的宽不小于长的，求总费用的最小值．

23.  本小题分
如图，在正方形中，点是对角线上一点不与点，重合，交于，连接，延长到使得，连接，，．
直接写出与的关系；
求的度数；
点是延长线上一点，交的延长线于点，连接交于点，若，如图，其他条件不变，直接写出的值．

 

24.  本小题分
如图，在平面直角坐标系中，直线与抛物线相交于，两点点在点的左侧，点关于轴的对称点为．
当时，直接写出，两点的坐标；
连接，，，，若的面积与的面积相等，求的值；
如图，将原抛物线先向右平移个单位，再向上平移个单位得到新的抛物线，点是轴正半轴上一点，，与新抛物线均有唯一公共点，异于原点，过点的直线交抛物线于点，，交直线于点，求的值．

答案和解析

1.【答案】 

【解析】解：的相反数是，
故选：．
根据“只有符号不同的两个数叫做互为相反数”解答．
本题考查了相反数，掌握相反数的定义是关键．
 

2.【答案】 

【解析】解：、图形旋转度后两部分不重合，不是中心对称图形，故本选项不合题意；
B、图形旋转度后两部分不重合，不是中心对称图形，故本选项不合题意；
C、图形旋转度后两部分重合，是中心对称图形，故本选项符合题意；
D、图形旋转度后两部分不重合，不是中心对称图形，故本选项不合题意．
故选：．
根据中心对称图形的概念对各选项分析判断即可得解．
本题考查了中心对称图形的概念，判断是否为中心对称图形是要寻找对称中心，之后观察图形旋转度后两部分是否重合．
 

3.【答案】 

【解析】解：、两张卡片的数字之和等于，是不可能事件；
B、两张卡片的数字之和等于，是随机事件；
C、两张卡片的数字之和大于或等于，是不可能事件；
D、两张卡片的数字之和等于，是不可能事件；
故选：．
根据事件发生的可能性大小判断．
本题考查的是必然事件、不可能事件、随机事件的概念．必然事件指在一定条件下，一定发生的事件．不可能事件是指在一定条件下，一定不发生的事件，不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件．
 

4.【答案】 

【解析】解：从左边看，共有两列，从左到右第一列是一个小正方形，第二列是三个小正方形．
故选：．
左视图是从左边看得出的图形，结合所给图形及选项即可得出答案．
此题考查了简单几何体的三视图，属于基础题，解答本题的关键是掌握左视图的观察位置．
 

5.【答案】 

【解析】

【分析】
本题考查了积的乘方．解题的关键是掌握积的乘方的运算方法，要注意理符号的变化．
根据积的乘方的法则进行计算即可．
【解答】
解：，
故选：．  

6.【答案】 

【解析】解：反比例函数中，，
此函数图象在二、四象限，
，
点，在第三象限，
函数图象在第四象限内随的增大而增大，
，
，
在第二象限，
，
、、的大小关系是，
故选：．
先根据函数解析式中的比例系数确定函数图象所在的象限，再根据各象限内点的坐标特点及函数的增减性解答．
本题考查了由反比例函数图象的性质判断函数图象上点的坐标特征，同学们应重点掌握．关键是根据反比例函数的增减性解题．
 

7.【答案】 

【解析】解：，是一元二次方程的两根，
，，



，

，
故选：．
根据，是一元二次方程的两根，可以得到，，把式子进行变形，整体代入计算即可．
本题考查了根与系数的关系，牢记“两根之和等于，两根之积等于”是解题的关键．
 

8.【答案】 

【解析】解：由题意可知，，两城相距千米，甲车比乙车先出发小时，却晚小时到城，
甲车的平均速度为：千米时，乙车的平均速度为：千米时，
设乙追上甲时，乙行驶的时间为小时，则：
，
解得，
，
两图象交点的纵坐标是．
故选：．
根据图象分别求出两车的速度，再列方程解答即可．
此题主要考查了一次函数的应用，关键是正确从函数图象中得到正确的信息．
 

9.【答案】 

【解析】解：如图，连接，，，，，分别交于点，点，过点作于点，
则，，
，，
四边形是正方形，
，
，，
，，
，，
∽，∽，
，，
即，，
解得，，
，，
，
，即，
，
在中，
，
，
故选：．
根据切线的性质，正方形的性质以及相似三角形的性质可求出，，进而求出，再根据三角形的面积可求出，由勾股定理可求出，由垂径定理可得．
本题考查圆周角定理、切线的性质以及勾股定理，掌握直角三角形的边角关系，圆周角定理，切线的性质以及相似三角形的性质是正确解答的前提．
 

10.【答案】 

【解析】解：令，
解得，，
时，则，
，
当时，；
当时，；
当时，；
函数值的和为：，
故选：．
令，解得，，然后可得当时函数值为，再分别求出，，时的函数值即可．
本题主要考查了函数图象上点坐标特征，通过去绝对值得到当时，是解决本题的关键．
 

11.【答案】 

【解析】解：本题答案不唯一：如等．
故答案为：．
由于无理数是无限不循环小数，根据此定义即可找出一个比小的无理数．
本题主要考查无理数的知识点，本题是一道开放性的试题，其中初中范围内学习的无理数有：，等；开方开不尽的数；以及像，等有这样规律的数．
 

12.【答案】 

【解析】解：万．
故答案为：．
科学记数法的表示形式为的形式，其中，为整数．确定的值时，要看把原数变成时，小数点移动了多少位，的绝对值与小数点移动的位数相同．当原数绝对值时，是正整数；当原数的绝对值时，是负整数．
此题考查科学记数法的表示方法．科学记数法的表示形式为的形式，其中，为整数，表示时关键要正确确定的值以及的值．
 

13.【答案】 

【解析】解：画树状图如下：

共有种等可能的结果，其中甲乙两位同学相邻的结果有种，
甲乙两人相邻的概率为，
故答案为：．
画树状图，共有种等可能的结果，其中甲乙两位同学相邻的结果有种，再由概率公式求解即可．
此题考查的是用树状图法求概率．树状图法可以不重复不遗漏的列出所有可能的结果，适合两步或两步以上完成的事件；用到的知识点为：概率所求情况数与总情况数之比．
 

14.【答案】 

【解析】解：，
，
在中，，
，
由旋转得：，
，
，
在中，，
故答案为：．
先利用平角定义求出，然后在中，利用含度角的直角三角形的性质求出的长，从而利用旋转的性质可得，再利用平角定义求出，最后在中，利用锐角三角函数的定义进行计算即可解答．
本题考查了解直角三角形的应用，熟练掌握锐角三角函数的定义是解题的关键．
 

15.【答案】 

【解析】解：抛物线的开口向上，则，对称轴在轴的左侧，则，交轴的负半轴，则，
，错误；
抛物线与轴的交点在正、负两个半轴上，且对称轴为直线，
时，，
，故正确；
抛物线的顶点坐标，
，，
，，
抛物线的解析式为，
抛物线交轴于，，
若方程两个根和且，则正确；
抛物线的解析式为，抛物线与轴的交点在与之间，
，
，故正确．
故答案为：．
根据抛物线图象判断参数符号判断，根据时，，可以判断正确，由顶点坐标可得、，进而判断；由，即可得到，解不等式组即可判断．
本题考查了二次函数图象与系数的关系：对于二次函数，二次项系数决定抛物线的开口方向和大小．当时，抛物线向上开口；当时，抛物线向下开口；一次项系数和二次项系数共同决定对称轴的位置．当与同号时即，对称轴在轴左；当与异号时即，对称轴在轴右．常数项决定抛物线与轴交点位置：抛物线与轴交于抛物线与轴交点个数由决定：时，抛物线与轴有个交点；时，抛物线与轴有个交点；时，抛物线与轴没有交点．
 

16.【答案】 

【解析】解：四边形上是矩形，，，
．
如图：以为斜边在上方构造等腰三角形，则，

以为圆心，的长为半径作圆，
，
点在上，连接，
则，
过点作于点，延长交于点，
则，，四边形、四边形均为矩形，
，，
，
在中，
，
，
．
 故答案为：．
根据矩形的性质可得以为圆心，的长为半径作圆，，点在上，连接，则，过点作于点，延长交于点，则，，四边形、四边形均为矩形，然后根据勾股定理及解三角形可得答案．
此题考查的是矩形的性质、解直角三角形、勾股定理等知识，正确作出辅助线，构造出等腰三角形是解决此题的关键．
 

17.【答案】     

【解析】解：解不等式，得：；
解不等式，得：；
把不等式和的解集在数轴上表示出来为：

原不等式组的解集为：．
故答案为：；
；
．
分别解这两个不等式，把不等式和的解集在数轴上表示出来，找到解集的公共部分即可得到原不等式组的解集．
本题考查了解一元一次不等式组，在数轴上表示不等式的解集，体现了数形结合的思想，在数轴上找到解集的公共部分是解题的关键．
 

18.【答案】证明：，
，
而，
，
，
；
解：，
，
，
而，
，∽，
． 

【解析】首先利用平行线的性质可以得到，然后利用已知条件即可证明，从而解决问题；
利用相似三角形的性质即可求解．
此题主要考查了相似三角形的性质，同时也利用了平行线的性质，熟练掌握相似三角形的性质与判定是解题的关键．
 

19.【答案】     

【解析】解：本次调查的样本容量是：，
在扇形统计图中，“玩游戏”对应的圆心角度数是，
条形统计图中“每周使用手机的时间小时以上”的人数是，
故答案为：，，；
人，
答：估计每周使用手机时间在小时以上不含小时的有人．
根据“查资料”的人数是人和所占的百分比，可以计算出样本容量，再根据扇形统计图中的数据可以计算出在扇形统计图中，“玩游戏”对应的圆心角度数；然后根据条形统计图中的数据，可以计算出条形统计图中“每周使用手机的时间小时以上”的人数；
根据条形统计图中的数据和中的结果，可以计算出每周使用手机时间在小时以上不含小时的人数．
本题考查条形统计图、样本容量、用样本估计总体、扇形统计图，解答本题的关键是明确题意，利用数形结合的思想解答．
 

20.【答案】解：证明：如图，连接，．
，
，
，
，
，
，
是直径，是的中点，
，
，
，即，
是半径，
是的切线．
解：过点作于点．
设，则，
在中，，
，
，
，
，
，
，
为的中点，
为的中点，即，，，
，
． 

【解析】本题属于圆综合题，考查了切线的判定，等腰三角形的性质等知识，解题的关键是学会添加常用辅助线，构造平行线解决问题，属于中考常考题型．
如图，连接，证明即可；
设，则，在中，，可得，证明，可得，，由此即可解决问题．
 

21.【答案】解：如图中，点，线段即为所求；
如图中，点，点即为所求．
 

【解析】取格点，，连接交与点，取格点，连接交与点，线段即为所求，利用等腰三角形的三线合一的性质，可得结论；
取格点，连接，取的中点，连接交与点，点即为所求．取格点，，连接交与点，连接，点即为所求证明∽，可得结论．
本题考查作图应用设计作图，解直角三角形，相似三角形的判定和性质，平行线等分线段定理等知识，解题的关键是灵活运用所学知识解决问题．
 

22.【答案】解：四边形是正方形，
，，
，分别是，的中点，
，
，
，
，
四边形是矩形，
，
是等腰直角三角形，
，
，
，
，
，
关于的函数关系式为：；
取正方形四边的中点，，，构成四边形，
，，
四边形是正方形，且面积，


；
由题意得：，
解得：或舍；
由题意得：，
解得：，
由知：，
． 

【解析】先根据长方形的面积长宽可得：关于的函数关系式，根据种植甲的费用种植乙的费用种植丙的费用可得：与的函数解析式；
根据种植总费用为元列方程：，解方程可得结论；
根据不小于长的列不等式，并结合中的取值可得答案．
本题考查二次函数的应用，解答本题的关键是明确题意，找出所求问题需要的条件，利用二次函数的性质解答．
 

23.【答案】解：，，理由如下：
，，，
≌，
，，
；
四边形是正方形，，
，，
，
是等腰直角三角形，
，，
，，
四边形为平行四边形，
，
由正方形性质可知，是等腰直角三角形，
，
，
又，
∽，
，
四边形为平行四边形，
，
即：，
；
由可知：是等腰直角三角形，是等腰直角三角形，
设，，
，，
，
，
，
，
，
，
，
∽，
，
，
，
． 

【解析】通过证明≌，可得，，可得结论；
通过证明∽，可得，由角的和差关系可求解；
通过证明∽，可得，由勾股定理可求的长，即可求解．
本题是相似形综合题，考查了正方形的性质，全等三角形的判定和性质，相似三角形的判定和性质，等腰直角三角形的性质等知识，灵活运用这些性质解决问题是解题的关键．
 

24.【答案】解：根据题意，得，
整理得到，
解方程，得，，
当时，；当时，；
点在点的左侧，
点的坐标为，点的坐标为；
，是抛物线图象上的点，
设，，则，
当时，
根据题意，得，
整理得到，
，是的两个根，
，，
设直线与轴的交点为，则点，
，，
，
，
，
，
，，
，
解得或舍去，
故．
当时，
根据题意，得，
整理得到，
，是的两个根，
，，
设直线与轴的交点为，则点，
，，
，
，
，
，
，，
，
解得或舍去，
故；
综上所述，的值为或；
由题意得：新的抛物线解析式为，
设点坐标为，点坐标为，
设：，
，
则：的两根为，
，
，
：，
同理：，
，
，，
，，
：，
设：：，
，
，
，
的两根为，，
，
 

【解析】解方程组，整理得到，解方程即可得到答案；
分和，两种情形求解，时，设，，直线与轴的交点为，，，，再结合根与系数关系求出的值，同理可求的情况；
利用待定系数法及一元二次方程根与系数关系，求出点，两点横坐标之间的关系，求出结论．
本题考查了抛物线与一次函数的交点问题，待定系数法，一元二次方程根与系数关系定理，熟练掌握二次函数与一次函数的交点，及其根与系数关系定理是解题的关键．