中考数学三轮冲刺《锐角三角函数实际问题》解答题冲刺练习13（含答案）

中考数学三轮冲刺《锐角三角函数实际问题》

解答题冲刺练习13

1.小明家的洗手盆上装有一种抬启式水龙头(如图1)，完全开启后，把手AM的仰角α＝37°，此时把手端点A、出水口B和点落水点C在同一直线上，洗手盆及水龙头的相关数据如图2.(参考数据：sin37°＝，cos37°＝，tan37°＝)

(1)求把手端点A到BD的距离；

(2)求CH的长.

2.如图是一辆小汽车与墙平行停放的平面示意图，汽车靠墙一侧OB与墙MN平行且距离为0.8米，已知小汽车车门宽AO为1.2米，当车门打开角度∠AOB为40°时，车门是否会碰到墙？请说明理由.(参考数据：sin40°≈0.64，cos40°≈0.77，tan40°≈0.84)

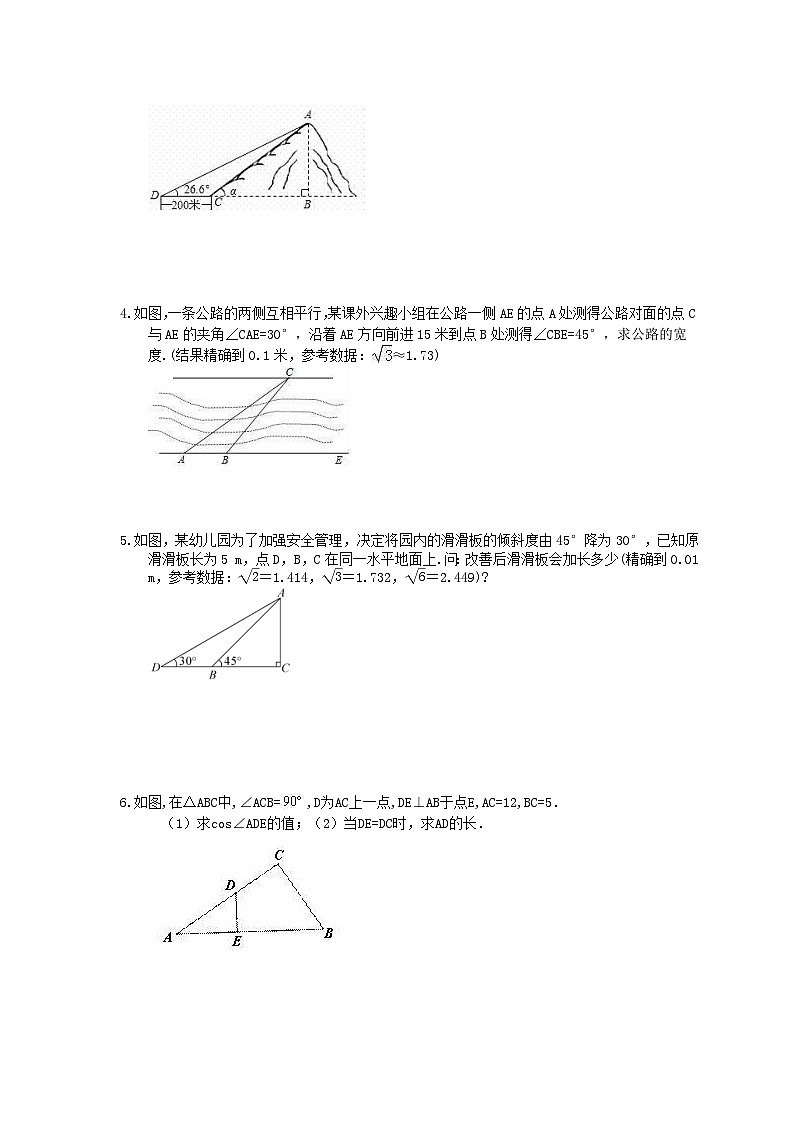
3.如图，小山岗的斜坡AC的坡度是tanα=，在与山脚C距离200米的D处，测得山顶A的仰角为26.6°，求小山岗的高AB（结果取整数：参考数据：sin26.6°=0.45，cos26.6°=0.89，tan26.6°=0.50）．

4.如图，一条公路的两侧互相平行，某课外兴趣小组在公路一侧AE的点A处测得公路对面的点C与AE的夹角∠CAE=30°，沿着AE方向前进15米到点B处测得∠CBE=45°，求公路的宽度.(结果精确到0.1米，参考数据：≈1.73)

5.如图，某幼儿园为了加强安全管理，决定将园内的滑滑板的倾斜度由45°降为30°，已知原滑滑板长为5 m，点D，B，C在同一水平地面上.问：改善后滑滑板会加长多少(精确到0.01 m，参考数据：＝1.414，＝1.732，＝2.449)?

6.如图,在△ABC中,∠ACB=,D为AC上一点,DE⊥AB于点E,AC=12,BC=5．

  （1）求cos∠ADE的值；（2）当DE=DC时，求AD的长．

7.为缓解“停车难”的问题，某单位拟建造地下停车库，建筑设计师提供了该地下车库的设计示意图（如图），按规定，地下车库坡道口上方要张贴限高标志，以便高职停车人车辆能否安全驶入.

（1）图中线段CD　　　填“是”或“不是”）表示限高的线段，如果不是，请在图中画出表示限高的线段；

（2）一辆长×宽×高位3916×1650×1465（单位：mm）的轿车欲进入车库停车，请通过计算，判断该汽车

能否进入该车库停车？（本小问中取1.7，精确到0.1）

8.如图所示，某公路检测中心在一事故多发地带安装了一个测速仪，检测点设在距离公路10 m的A处，测得一辆汽车从B处行驶到C处所用的时间为0.9秒.已知∠B=30°，∠C=45°.

(1)求B，C之间的距离；(保留根号)

(2)如果此地限速为80 km/h，那么这辆汽车是否超速？请说明理由.

(参考数据：≈1.7，≈1，4)

9.如图1是一副创意卡通圆规，图2是其平面示意图，OA是支撑臂，OB是旋转臂，使用时，以点A为支撑点，铅笔芯端点B可绕点A旋转作出圆.已知OA=OB=10 cm.

(1)当∠AOB=20°时，求所作圆的半径；(结果精确到0.01 cm)

(2)保持∠AOB=20°不变，在旋转臂OB末端的铅笔芯折断了一截的情况下，作出的圆与(1)中所作圆的大小相等，求铅笔芯折断部分的长度.(结果精确到0.01 cm)

(参考数据：sin10°≈0.174，cos10°≈0.985，sin20°≈0.342，cos20°≈0.940)

10.如图①，AB为半圆的直径，O为圆心，C为圆弧上一点，AD垂直于过C点的切线，垂足为D，AB的延长线交直线CD于点E.

(1)求证：AC平分∠DAB；

(2)若AB=4，B为OE的中点，CF⊥AB，垂足为点F，求CF的长；

(3)如图②，连接OD交AC于点G，若=，求sinE的值.

0.中考数学三轮冲刺《锐角三角函数实际问题》解答题冲刺练习13（含答案）参考答案

一         、解答题

1.解：(1)过点A作AN⊥BD于点N，过点M作MQ⊥AN于点Q，

在Rt△AMQ中，AB=10,sinα=.

∴，∴，

∴AN＝AQ＋Q＝12.

(2)根据题意：NB∥GC.

∴△ANB～△AGC.

∴，

∵MQ＝DN＝8，

∴BN＝DB﹣DN＝4，

∴.

∴GC＝12，

∴CH＝30﹣8﹣12＝10.

答：CH的长度是10cm.

2.解：过A作AC⊥OB于点C，

在Rt△AOC中，∠AOC=40°，

∴sin40°=.

又∵AO=1.2米，

∴AC=OA·sin40°≈1.2×0.64=0.768(米).

∵AC=0.768米＜0.8米，

∴车门不会碰到墙.

3.解答： 解：∵在直角三角形ABC中，=tanα=，

∴BC=

∵在直角三角形ADB中，

∴=tan26.6°=0.50即：BD=2AB

∵BD﹣BC=CD=200∴2AB﹣AB=200

解得：AB=300米，

答：小山岗的高度为300米．

4.解：如图，过点C作CD⊥AE于点D，

设公路的宽CD=x米，

∵∠CBD=45°，

∴BD=CD=x，

在Rt△ACD中，∵∠CAE=30°，

∴tan∠CAD==，即=，

解得：x=≈20.5(米)，

答：公路的宽为20.5米.

5.解：在Rt△ABC中，∵AB＝5，∠ABC＝45°，

∴AC＝AB·sin45°＝5×＝(m).

在Rt△ADC中，∵∠ADC＝30°，

∴AD＝2AC＝5 ≈5×1.414＝7.07(m)，

∴AD﹣AB＝7.07﹣5＝2.07(m).

答：改善后滑滑板约会加长2.07 m.

6.解：如图，（1）∵DE⊥AB，∴∠DEA=90°．∴∠A+∠ADE=90°．

∵∠ACB=，∴∠A+∠B=90°．∴∠ADE=∠B．

在Rt△ABC中，∵AC=12，BC=5，∴AB=13．∴．∴．

（2）由（1）得，设为，则．

∵ ，∴ . 解得.∴ .

7.解：

8.解：(1)过点A作AD⊥BC于点D，则AD=10 m.

∵在Rt△ACD中，∠C=45°，

∴CD=AD=10 m.

在Rt△ABD中，tanB=，

∵∠B=30°，

∴=.

∴BD=10 m.

∴BC=BD＋DC=(10＋10)m.

答：B，C之间的距离是(10＋10)m.

(2)这辆汽车超速，理由如下：

由(1)知BC=(10＋10)m≈27 m.

∴汽车速度为=30(m/s)=108 km/h.

∵108＞80，

∴这辆汽车超速.

9.解：(1)连接BA，作OC⊥AB于点C.

由题意可得，OA=OB=10 cm，∠OCB=90°，∠AOB=20°，

∴∠BOC=10°.

∴AB=2BC=2OB·sin10°≈2×10×0.174≈3.5(cm)，

即所作圆的半径约为3.5 cm.

(2)作AD⊥OB于点D，作AE=AB.

∵保持∠AOB=20°不变，则折断的部分为BE.

∵∠AOB=20°，OA=OB，∠ODA=90°，

∴∠OAB=80°，∠OAD=70°.

∴∠BAD=10°.

∴BE=2BD=2AB·sin10°≈2×3.5×0.174≈1.2(cm)，

即铅笔芯折断部分的长度是1.2 cm.

10. (1)证明：连接OC，如图①.

∵OC切半圆O于C，

∴OC⊥DC，

又AD⊥CD.

∴OC∥AD.

∴∠OCA=∠DAC.

∵OC=OA，

∴∠OAC=∠ACO.

∴∠DAC=∠CAO，即AC平分∠DAB.

(2)解：在Rt△OCE中，∵OC=OB=OE，∴∠E=30°.

∴在Rt△OCF中，CF=OC·sin60°=2×=.

(3)解：连接OC，如图②.

∵CO∥AD，∴△CGO∽△AGD.∴==.

不妨设CO=AO=3k，则AD=4k.

又△COE∽△DAE，∴===.∴EO=9k.

在Rt△COE中，sinE===.