

中考数学三轮冲刺《锐角三角函数实际问题》解答题冲刺练习04(含答案)
展开中考数学三轮冲刺《锐角三角函数实际问题》
解答题冲刺练习04
1.如图,海上有一灯塔P,在它周围3海里处有暗礁,一艘客轮以9海里/时的速度由西向东航行,行至A点处测得P在北偏东60°方向上,继续行驶20分钟后,到达B处又测得灯塔P在北偏东45°方向上,问客轮不改变方向继续前进有无触礁危险?
2.如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到P处再测得点C的仰角为45°,已知OA=100米,山坡坡度(竖直高度与水平宽度的比)i=1:2,且O、A、B在同一条直线上.求电视塔OC的高度以及此人所在位置点P的铅直高度.(测倾器高度忽略不计,结果保留根号形式)
3.如图,一艘轮船以每小时40海里的速度在海面上航行,当该轮船行驶到B处时,发现灯塔C在它的东北方向,轮船继续向北航行,30分钟后到达A处,此时发现灯塔C在它的北偏东75°方向上,求此时轮船与灯塔C的距离.(结果保留根号)
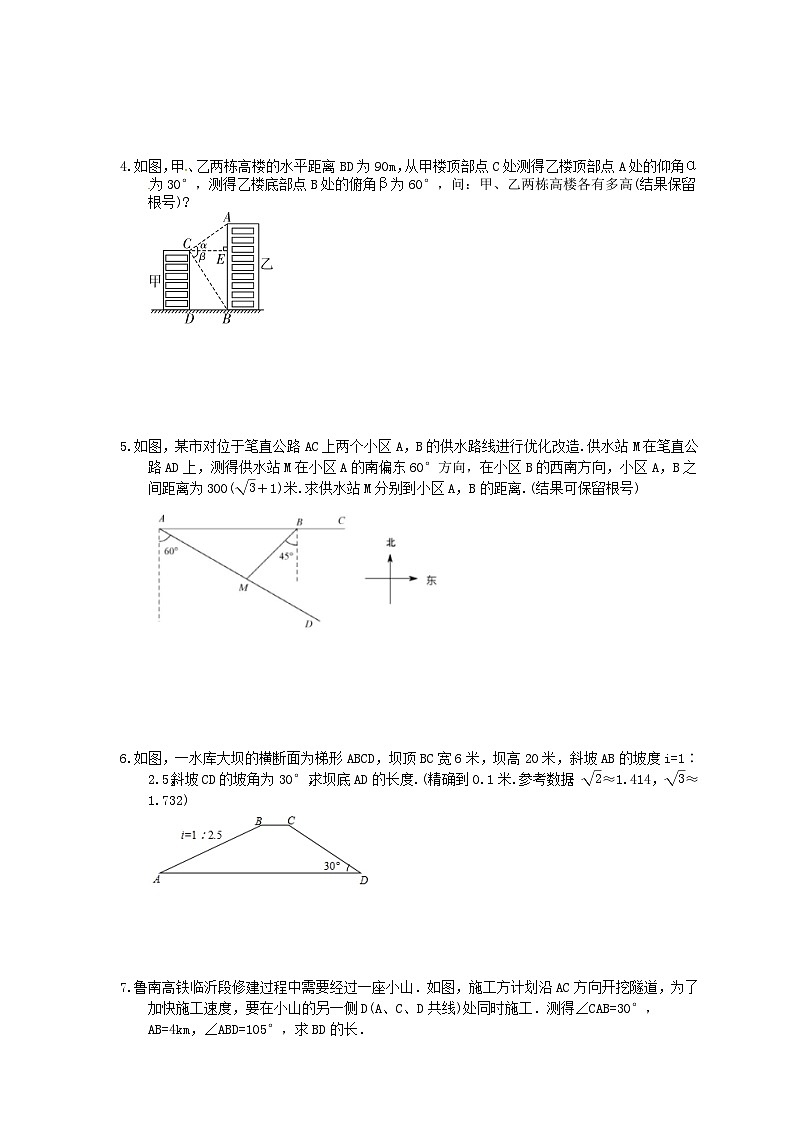
4.如图,甲、乙两栋高楼的水平距离BD为90m,从甲楼顶部点C处测得乙楼顶部点A处的仰角α为30°,测得乙楼底部点B处的俯角β为60°,问:甲、乙两栋高楼各有多高(结果保留根号)?
5.如图,某市对位于笔直公路AC上两个小区A,B的供水路线进行优化改造.供水站M在笔直公路AD上,测得供水站M在小区A的南偏东60°方向,在小区B的西南方向,小区A,B之间距离为300(+1)米.求供水站M分别到小区A,B的距离.(结果可保留根号)
6.如图,一水库大坝的横断面为梯形ABCD,坝顶BC宽6米,坝高20米,斜坡AB的坡度i=1∶2.5,斜坡CD的坡角为30°,求坝底AD的长度.(精确到0.1米.参考数据:≈1.414,≈1.732)
7.鲁南高铁临沂段修建过程中需要经过一座小山.如图,施工方计划沿AC方向开挖隧道,为了加快施工速度,要在小山的另一侧D(A、C、D共线)处同时施工.测得∠CAB=30°,AB=4km,∠ABD=105°,求BD的长.
8.某校的教室A位于工地O的正西方向,且OA=200m,一台拖拉机从O点出发,以每秒5m的速度沿北偏西53°的方向行驶,设拖拉机的噪声污染半径为130m,则教室A是否在拖拉机的噪声污染范围内?若不在,请说明理由;若在,求出教室A受噪声污染的时间有几秒.(参考数据:sin53°≈0.80,sin37°≈0.60,tan37°≈0.75)
9.如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.
10.如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上从点A运动到点B,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.
(1)求证:CE=CF;
(2)求线段EF的最小值;
(3)当点D从点A运动到点B时,试求线段EF扫过的面积(直接写出结果).
0.中考数学三轮冲刺《锐角三角函数实际问题》解答题冲刺练习04(含答案)参考答案
一 、解答题
1.解:过P作PC⊥AB于C点,如图,
据题意知AB=9×=3,∠PAB=90°﹣60°=30°,[来源:学&科&网Z&X&X&K]
∠PBC=90°﹣45°=45°,∠PCB=90°,
∴PC=BC.
在Rt△APC中,tan 30°===,
即=,
∴PC=海里>3海里,
∴客轮不改变方向继续前进无触礁危险.
2.解:作PE⊥OB于点E,PF⊥CO于点F,
在Rt△AOC中,AO=100,∠CAO=60°,
∴CO=AO•tan60°=100(米).
设PE=x米,
∵tan∠PAB=0.5,
∴AE=2x.
在Rt△PCF中,∠CPF=45°,CF=100﹣x,PF=OA+AE=100+2x,
∵PF=CF,
∴100+2x=100﹣x,解得x=(米).
答:电视塔OC高为100米,点P的铅直高度为(米).
3.解:过点A作AD⊥BC于点D.
由题意,AB=×40=20(海里)
∵∠PAC=∠B+∠C,
∴∠C=∠PAC﹣∠B=75°﹣45°=30°,
在Rt△ABD中,sinB=,
∴AD=AB•sinB=20×=10(海里),
在Rt△ACD中,∵∠C=30°,
∴AC=2AD=20(海里),
答:此时轮船与灯塔C的距离为20海里.
4.解:由题意,得CE=BD=90m.
在Rt△ACE中,tanα=,
∴AE=CE·tanα=30 m.
在Rt△BCE中,tanβ=,
∴BE=CE·tanβ=90 m.
∴CD=BE=90 m,
AB=AE+BE=30 +90 =120 m.
∴甲楼高90 m,乙楼高120 m.
5.解:作ME⊥AB,垂足为E.设ME=x米.
在Rt△AME中,∠MAE=90°-60°=30°,
∴AM=2ME=2x, AE==x.
在Rt△BME中,∠MBE=90°-45°=45°,
∴ME=EB=x,MB=x.
∵AE+BE=AB=300(+1),
即x+ x=300(+1),解得x=300.
∴AM=2ME=2x=600,
MB=x=300.
答:供水站M到小区A,B的距离分别是600米、300米.
6.解:作BE⊥AD,CF⊥AD,垂足分别为点E,F,则四边形BCFE是矩形.
由题意,得BC=EF=6米,BE=CF=20米,
∵斜坡AB的坡度i为1∶2.5,BE=20米,
∴=.∴AE=50米.
在Rt△CFD中,∠D=30°,
∴DF==20米.
∴AD=AE+EF+FD=50+6+20≈90.6(米).
答:坝底AD的长度约为90.6米.
7.解:作BE⊥AD于点E,
∵∠CAB=30°,AB=4km,
∴∠ABE=60°,BE=2km,
∵∠ABD=105°,
∴∠EBD=45°,
∴∠EDB=45°,
∴BE=DE=2km,
∴BD==2km,
即BD的长是2km.
8.解:如图,过点A作AB⊥OM于点B,
∵∠MON=53°,
∴∠AOM=90°﹣53°=37度.
在Rt△ABO中,∠ABO=90°,[来源:学*科*网]
∵sin∠AOB=,
∴AB=AO•sin∠AOB=200×sin37°≈120(m).
∵120m<130m.
∴教室A在拖拉机的噪声污染范围内.
根据题意,在OM上取C,D两点,连接AC,AD,使AC=AD=130m,
∵AB⊥OM,
∴B为CD的中点,即BC=DB,
∴BC==50(m),∴CD=2BC=100(m).
即影响的时间为=20(s).
9.【解答】解:过点D作l1的垂线,垂足为F,
∵∠DEB=60°,∠DAB=30°,∴∠ADE=∠DEB﹣∠DAB=30°,
∴△ADE为等腰三角形,∴DE=AE=20,
在Rt△DEF中,EF=DE•cos60°=20×=10,
∵DF⊥AF,∴∠DFB=90°,∴AC∥DF,
由已知l1∥l2,∴CD∥AF,∴四边形ACDF为矩形,CD=AF=AE+EF=30,
答:C、D两点间的距离为30m.
10.
中考数学三轮冲刺《锐角三角函数实际问题》解答题冲刺练习15(含答案): 这是一份中考数学三轮冲刺《锐角三角函数实际问题》解答题冲刺练习15(含答案),共8页。试卷主要包含了3,cs20°≈0,50海里,8×≈5,4,解得x=70,等内容,欢迎下载使用。
中考数学三轮冲刺《锐角三角函数实际问题》解答题冲刺练习13(含答案): 这是一份中考数学三轮冲刺《锐角三角函数实际问题》解答题冲刺练习13(含答案),共9页。试卷主要包含了8米,已知小汽车车门宽AO为1,6°,求小山岗的高AB.,7,精确到0,07﹣5=2,5 cm等内容,欢迎下载使用。
中考数学三轮冲刺《锐角三角函数实际问题》解答题冲刺练习12(含答案): 这是一份中考数学三轮冲刺《锐角三角函数实际问题》解答题冲刺练习12(含答案),共8页。试卷主要包含了41,eq \r≈1,1海里),0,等内容,欢迎下载使用。












