北师大版八年级上册4 平行线的性质课文ppt课件

这是一份北师大版八年级上册4 平行线的性质课文ppt课件，共13页。PPT课件主要包含了复习回顾，复习巩固，例1如图，BF∥CE，AM∥BF，AC∥DM，独立探究步骤规范，答GH∥MN，反思提高等内容，欢迎下载使用。

学习目标：1，使学生掌握平行线的三个性质，并能应用它们进行简单的推理论证。2，使学生经过对比后，理解平行线的性质和判定的区别和联系。3，通过推理论证，培养学生的分析问题和解决问题的能力4，培养学生逆向思维的能力。重点：1,平行线的三个性质及其应用。2,几何证明格式的规范性。难点：正确理解性质和判定的区别和联系以及运用它们去推理证明。
问题1: 平行线的性质有哪几条？问题2：判别直线平行的条件有哪几个？ 你现在一共有几个判定直线平行的方法？问题3：在应用二者时应注意什么问题?
如图，直线a，b被直线c所截，（1）当∠1=∠2时,你能结合 图形用推理的方式来说明 a∥b吗？
∵ ∠1=∠2（已知）
∴a∥b(内错角相等，两直线平行)
∵ ∠2+∠3=1800（已知）
∴a∥b(同旁内角互补，两直线平行)
（2）若∠2+∠3=180°呢？
（1）若∠1=∠2，可以判定哪两条直线平行？根据是什么？
（2）若∠2=∠M，可以判定哪两条直线平行？根据是什么？
（3）若∠2 +∠3=180°，可以判定哪两条直线平行？根据是什么？
内错角相等，两直线平行。
同位角相等，两直线平行。
同旁内角互补，两直线平行。
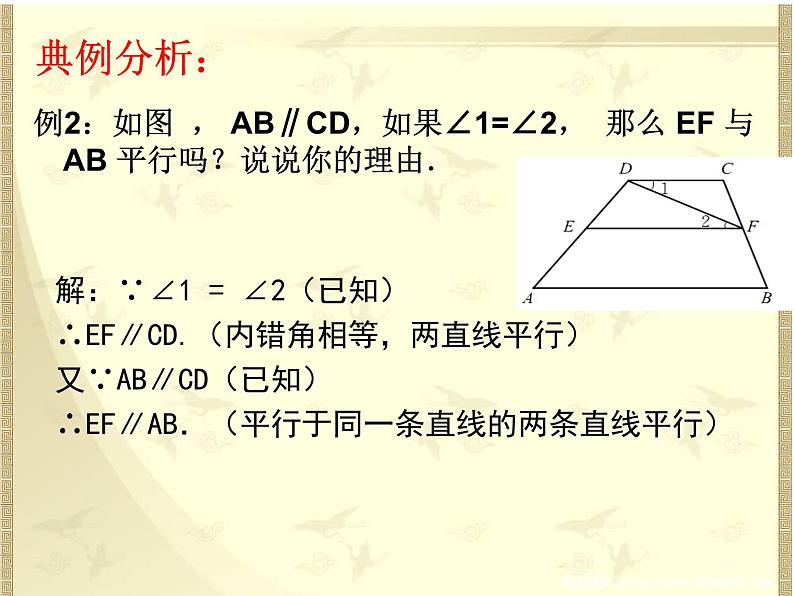
例2：如图 ， AB∥CD，如果∠1=∠2， 那么 EF 与 AB 平行吗？说说你的理由．
解：∵∠1 = ∠2（已知）∴EF∥CD.（内错角相等，两直线平行）又∵AB∥CD（已知）∴EF∥AB．（平行于同一条直线的两条直线平行）
例3：如图，已知直线a∥b，直线c∥d，∠1=107°，求∠2，∠3 的度数.
解：∵a∥b（已知） ∴∠2 = ∠1 = 107°（两直线平行，内错角相等） ∵c∥d（已知） ∴∠1 ＋ ∠3 = 180°（两直线平行，同旁内角互补） ∴∠3 = 180°- ∠1 = 180°-107°= 73°（等量代换）
如图，AE∥CD，若∠1 = 37°，∠D=540，求∠2 和∠BAE的度数.
解：∵ AE∥CD （已知） ∴∠2 =∠1= 37°（两直线平行，内错角相等） ∠BAE=∠D=540（两直线平行，同位角相等）
课堂练习：及时巩固，深化提高
1：如图,选择合适的内容填空。（1）因为AB//CD 所以∠1=∠2（ ）（2）因为∠3＝∠1 所以 //____（同位角相等，两直线平行） （3）因为∠1＋∠ ＝180 ，所以AB//CD（ ）
两直线平行，内错角相等
同旁内角互补，两直线平行
2：如图，∠1=∠3，那么，∠1和∠2的大小有何关系？∠1和∠4的大小有何关系？为什么？由此你得到什么结论？
解：∵ ∠1=∠3（已知） ∴AB∥CD（同位角相等，两直线平行） ∴∠1=∠2（两直线平行，内错角相等） ∠1+∠4=1800（两直线平行，同旁内角互补）
结论：两直线被第三条直线所截，如果同位角相等，那么内错角相等，同旁内角互补。
问题3：如图，平行直线AB,CD被直线EF所截，分别交直线AB,CD于点G,M。GH和MN分别是∠EGB和∠EMD的角平分线。问：GH和MN平行吗？请说明理由。
理由：∵AB∥CD（已知） ∴∠EGB=∠EMD（两直线平行，同位角相等）∵GH和MN分别是∠EGB和∠EMD的角平分线（已知）∴∠EGH= ∠EGB，∠EMN= ∠EMD（角平分线性质）∴∠EGH=∠EMN（等量代换）∴GH∥MN（同位角相等，两直线平等）
1、本节课主要应用了哪些知识？2、在应用它们时，你认为应该注意哪些问题？3、在写几何推理的过程中，因为和所以分 别表达的意义是什么？根据是什么？