2023届中考数学考向信息卷 天津专版

2023届中考数学考向信息卷

天津专版

【满分：120】

一、选择题（本大题共12小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的）

1.-5 的相反数是(   )

A. 5 B.  C. -5 D.

2.如图是运动会领奖台，它的俯视图是(   )

A. B. C. D.

3.2020年，新冠肺炎疫情席卷全球，截至2022年5月14日，累计确诊人数超过520000000例，抗击疫情成为全人类共同的战役.确诊病例“520000000”用科学记数法可表示为(   )

A. B. C. D.

4.如图，，，则(   )

A. B. C. D.

5.如图，在平面直角坐标系中，以原点为位似中心，将扩大到原来的2倍，得到.若点A的坐标是，则点的坐标是(   )

A. B. C. D.

6.，，5三个数的大小关系是(   )

A. B. C. D.

7.已知一元二次方程 有两个相等的实数根, 且a,b 均为整数, 则a,b的值可能是(   )

A.,  B.,

C.,  D.,

8.下列运算正确的是(   )

A.  B.

C.  D.

9.关于一次函数，下列结论正确的是(   )

A.y随x的增大而增大 B.当时，

C.图象经过第一、第二、第四象限 D.图象与x轴交于点

10.如图，AB，BC为的两条弦，连接OA，OC，点D为AB的延长线上一点，若，则的度数为(   )

A.100° B.118° C.124° D.130°

11.如图，在中，，将绕顶点C逆时针旋转得到，M是BC的中点，P是的中点，连接PM.若，，则线段PM的最大值是(   )

A.4 B.3 C.2 D.1

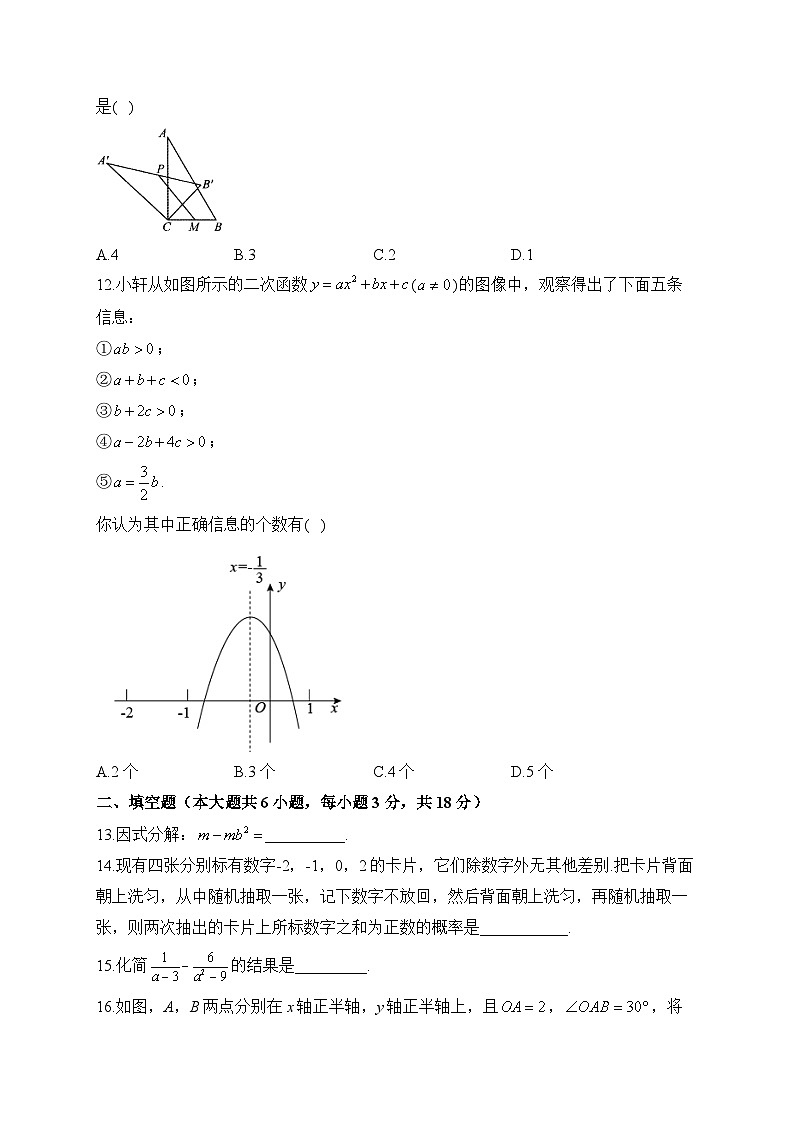
12.小轩从如图所示的二次函数()的图像中，观察得出了下面五条信息：

①；

②；

③；

④；

⑤.

你认为其中正确信息的个数有(   )

A.2个 B.3个 C.4个 D.5个

二、填空题（本大题共6小题，每小题3分，共18分）

13.因式分解：__________.

14.现有四张分别标有数字-2，-1，0，2的卡片，它们除数字外无其他差别.把卡片背面朝上洗匀，从中随机抽取一张，记下数字不放回，然后背面朝上洗匀，再随机抽取一张，则两次抽出的卡片上所标数字之和为正数的概率是___________.

15.化简的结果是_________.

16.如图，A，B两点分别在x轴正半轴，y轴正半轴上，且，，将沿AB翻折得，反比例函数的图像恰好经过D点，则k的值为_______.

17.如图，正方形ABCD和正方形AEFG的边长分别为和，点E、G分别为AB、AD边上的点，H为CF的中点，连接HG，则HG的长为___________cm.

18.甲、乙两人手里分别有x 张、y 张优惠券.

(1) 若,, 甲给了乙 张优惠券后, 则乙优惠券的总数比甲剩余的少张.

(2) 乙对甲说:“如果我给你 1 张优惠券, 那么你的数量就是我的 2 倍. ”则x ______y (填“>”或 “<”). 甲对乙说: “如果我给你 3 张优惠券, 那么你的数量就是我的 2 倍. ”根据甲、乙的说法, 可知甲原本有________张优惠券.

三、解答题（本大题共7小题，共66分.解答应写出文字说明、演算步骤或推理过程）

19.（8分）已知:关于x的不等式组

(1)若该不等式组的解集为, 则a的值为_________.

(2) 若该不等式组只有两个整数解, 则a的取值范围是__________.

20.（8分）2022 年 3 月 23 日下午, “天宫课堂” 第二课开讲,“太空教师” 翟志刚、王亚平、叶光富在 中国空间站再次为广大青少年带来一堂精彩的太空科普课. 三位航天员相互配合, 生动演示了太空 “冰雪” 实验、液桥演示实验、水油分离实验、太空抛物实验 (依次记为A,B,C,D ). 某校九 (1) 班在教 室观看了这堂科普课, 为了解同学们对这四个实验的喜爱情况, 课外兴趣小组对全班同学进行了调 查, 并根据调查结果绘制出如下统计图表 (不完整). 赵老师查看后指出, 条形统计图中男生人数有 一处错误.

根据以上信息, 解答下列问题.

(1)喜欢哪个实验的男生人数有误? 并直接写出正确的人数.

(2)喜欢实验A 的女生人数为________ , _________.

(3)兰兰想用扇形统计图反映喜欢各个实验的人数占全班总人数的百分比, 是否可行? 若可行, 求 出C 对应扇形圆心角的度数; 若不可行, 请说明理由.

21.（10分）如图，西安某中学依山而建，校门A处有一坡度的斜坡，长度为13米，在坡顶B处看教学楼的楼顶C的仰角，离B点4米远的E处有一个花台，在E处仰望C的仰角是，的延长线交校门处的水平面于点D，求楼顶C的高度.(结果保留根号)

22.（10分）如图，在中，对角线AC，BD交于点O，E是AD上一点，连接EO并延长，交BC于点F.连接AF，CE，EF平分.

(1)求证：四边形AFCE是菱形；

(2)若，，求四边形AFCE的面积.

23.（10分）某医药研究所开发了一种新药, 在试验药效时发现, 如果成人按规定剂量服用, 每毫升血液中含药 量 y (微克) 随时间x (小时) 的变化情况如图所示, 那么当成人按规定剂量服用后, 根据图象回答下 列问题.

(1)服药后_______小时, 血液中含药量最高;

(2)求当时, y关于x 的函数解析式;

(3)如果每毫升血液中含药量为 3 微克或 3 微克以上时治疗疾病药效最好,那么服药后药效最好的 时长是多少小时?

24.（10分）如图, D是以AB 为直径的上一点, 过点D 的切线DE 交AB 的延长线于点E, 过点B 作 交AD 的延长线于点C, 垂足为点F.

(1)求证:.

(2)若的直径AB 为9，.

①求线段 BF的长;

②求线段BE 的长.

25.（10分）如图1，已知抛物线交y轴于点A，交x轴于点，点P是抛物线上一动点，过点P作x轴的垂线l，再过点A作l的垂线，垂足为Q，连接AP.

(1)___________；

(2)在y轴右侧的抛物线上是否存在一点P，使？若存在，请求出符合条件的点P的横坐标：若不存在，请说明理由，

(3)如图2，当点P位于抛物线的对称轴的右侧时，若将沿AP翻折，点Q的对应为点，请直接写出当点落在坐标轴上时点P的坐标.

答案以及解析

1.答案：A

解析：只有符号不同的两个数互为相反数. 故 -5 的相反数为5 .

2.答案：D

解析：领奖台的俯视图是：

故选：D.

3.答案：B

解析：，故选：B.

4.答案：B

解析：如图，

，，

，

，

故选：B.

5.答案：C

解析：如题图所示，，

，

，

，即.

故选C.

6.答案：C

解析：因为，，且，

所以即，

故选：C.

7.答案：D

解析： 一元二次方程 有两个 相等的实数根,，. 又 ，，, 故只有D 选项符合题意.

8.答案：B

解析： ，，. 故选 B.

9.答案：C

解析：A.一次函数中，故此函数值y随x的增大而减小，即A项错误，不符合题意；

B.把代入得：，即B项错误，不符合题意；

C.一次函数中，故函数图象经过第一、二、四象限，即C项正确，符合题意；

D.把代入得：，图象与x轴交于点，即D项错误，不符合题意，故选C.

10.答案：C

解析：如图，在优弧AC上取点P，连接PA，PC，

，

，

，

故选：C.

11.答案：B

解析：如图，连接PC.在中，，，，根据旋转不变性可知，，，又，，，又，，PM的最大值为3（此时P，C，M共线）.故选B.

12.答案：D

解析：①如图，抛物线开口方向向下，

.

对称轴，

.

.故①正确，符合题意.

②如图，当时，，即.故②正确，符合题意.

③如图，当时，，，即..故③正确，符合题意.

④如图，当时，，即，

抛物线与y轴交于正半轴，.

，.

，即.故④正确，符合题意.

⑤如图，对称轴，则.故⑤正确，符合题意.

综上所述，正确的结论是①②③④⑤，共5个.

故选D.

13.答案：

解析：原式

.

故答案为：.

14.答案：

解析：列表如下：

由表可知，共有12种等可能结果，其中两次抽出的卡片上所标数字之和为正数的有4种结果，

所以两次抽出的卡片上所标数字之和为正数的概率为.

故答案为：.

15.答案：

解析：原式

16.答案：

解析：将沿AB翻折得，

，，

，

过D作于C，

，

，，

，

，

反比例函数的图像恰好经过D点，

，

故答案为：.

17.答案：

解析：如图所示，延长GH交DC的延长线于N，

正方形ABCD和正方形AEFG的边长分别为5cm和3cm，

，，，

，，

点H是CF的中点，

，

在和中，

，

，

，，

，

在中，有勾股定理可得：，

.

故答案为：.

18.答案：(1)

(2)>,7

解析：(1).

(2) 由乙说的话可得 ①, 整理, 得 ， , 又，，. 由甲说的话可得 ②, 联立①②可得，.

19.答案：(1)3

(2)

解析：(1) 解, 得; 解, 得 ，不等式组的解集为，，.

 (2) 由 (1) 可知不等式组 的解集为, 若不等式组只有两个整数解, 则整数解为3,4，，.

20.答案： (1)喜欢实验D 的男生人 数有误.正确的人数应为 12 .

(2) 12, 40

(3) 不可行.理由见解

解析:(1), 而,

答案为:6 不是整数,故喜欢实验 D 的男生人数有误.

全班总人数为,

故喜欢实验 D的男生人数为.

(2),.

(3)不可行.理由:由统计表可知, , 即喜欢各个实验的人数占全班总人数的百 分比之和大于1,, 即喜欢实验A 的人数和喜欢实验D 的人数之和大于全班总人数.

21.答案：的长度为米

解析：过点B作，过点E作，

，

，

米，

米，米，

米，

设为x米，则米，

，

米，

，

，

米，

米，

米，

答：的长度为米.

22.答案：(1)证明见解析

(2)

解析：(1)证明：四边形ABCD是平行四边形，

，，，

在和中，，

，，

，四边形AFCE是平行四边形，

EF平分，，

，，

平行四边形四边形AFCE是菱形，四边形AFCE是菱形；

(2)解：由(1)得：四边形AFCE是菱形，

，，，，

，，

，是等边三角形，，

，，

四边形AFCE的面积为：.

23.答案： (1)2

(2)

(3) 4 小时

解析：(1)略

(2) 当 时, 设y 关于x 的函数解析式是,

点 ， 在该函数图象上,

解得

即 y关于x 的函数解析式是.

(3)当 时, 设 y关于 x的函数关系式为,

点 在该函数图象上, ,

解得,

即当 时, y关于x 的函数关系式为.

将 代人, 得,

解得.

由函数图象可知当 时,， (小时)，

故服药后药效最好的时长是 4 小时.

24.答案： (1)见解析

(2)①1②

解析： (1) 证明: 如图, 连接OD.

DE是的切线,

，

，

，

，

，

，

，

(2)①如图, 连接BD, 则.

，，

，，

，

，

，，

②由 (1) 知,

,

, 即.

25.答案：(1)3

(2)或

(3)或或

解析：(1)把代入，

得，解得，

故答案为：3.

(2)存在，理由如下：

如图1，作点C关于点O的对称点D，连接AD，

由对称性可知，，即.

过点C作于点E，

，，

，.

，

即，

解得，

在中，，，

由勾股定理可得，

.

，即，

设，则，

，

点P在抛物线上，

，解得(舍去)或.

作点P关于直线AQ的对称点M，则直线AM与抛物线的交点即为点P，

由上可知，，，

直线AM的解析式为：，

令，解得.

综上，点P的横坐标为或.

(3)设

当点落在x轴上，延长QP交x轴于H，如图2，

则，

沿AP对折，点Q的对应点为点，

，

，

，

，

，

，即，

解得，

，

在中，，

整理得，解得，，

此时P点坐标为或；

当点落在y轴上，则点A、、P、Q所组成的四边形为正方形，

，

即，

解方程得(舍去)，，

此时P点坐标为；

解方程得(舍去)，，

此时P点坐标为，

综上所述，点P的坐标为或或.