2023届中考数学考向信息卷 山西专版

2023届中考数学考向信息卷

山西专版

【满分：120】

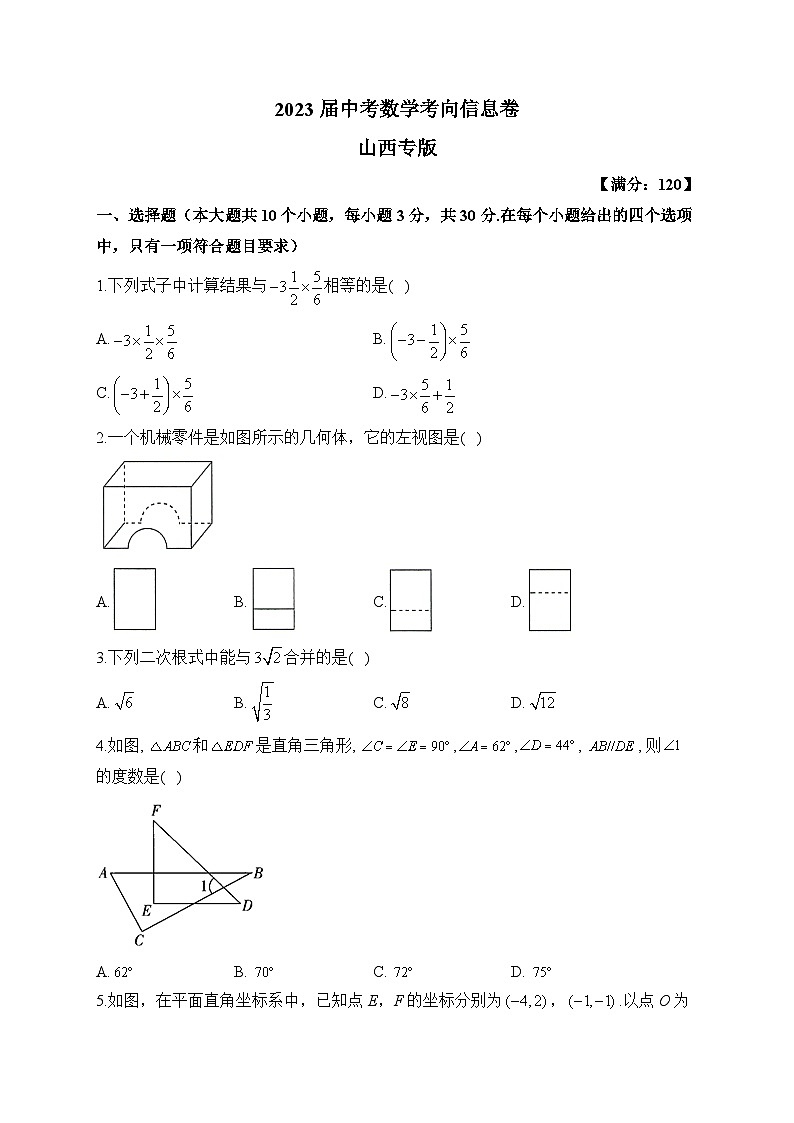
一、选择题（本大题共10个小题，每小题3分，共30分.在每个小题给出的四个选项中，只有一项符合题目要求）

1.下列式子中计算结果与相等的是(   )

A.  B.

C.  D.

2.一个机械零件是如图所示的几何体，它的左视图是(   )

A. B. C. D.

3.下列二次根式中能与合并的是(   )

A. B. C. D.

4.如图, 和是直角三角形, ,,, , 则的度数是(   )

A. B.  C.  D.

5.如图，在平面直角坐标系中，已知点E，F的坐标分别为，.以点O为位似中心，在原点的另一侧按的相似比将缩小，则点E的对应点的坐标为(   )

A. B. C. D.

6.若关于x，y的二元一次方程组的解互为相反数，则k的值是(   )

A.4 B.3 C.2 D.1

7.冬修水利正当时，“通经活络”惠民生.广元市双峡湖水库灌区工程现已进入全面建设阶段，预计明年6月底全部完工.为了按时完工，施工队抢抓施工黄金时间节点，并增加了人力进行管道铺设.已知增加人力后平均每小时比原计划多铺设10m，现在铺设120m所需时间与原计划铺设90m所需时间相同.设增加人力后平均每小时铺设xm，根据题意可列方程为(   )

A. B. C. D.

8.某校举行防疫知识竞赛，甲、乙两班的参加人数及成绩(满分100分)的平均数、中位数、方差如下表

所示，规定成绩大于或等于96分为优异.

佳佳根据上述信息得出如下结论：

①甲、乙两班学生成绩的平均水平相同；

②甲班的成绩比乙班的成绩稳定；

③乙班成绩优异的人数比甲班多；

④佳佳得94分将排在甲班的前20名.

其中正确的结论是(   )

A.①② B.①④ C.③④ D.①③④

9.如图，直线与双曲线相交于A，B两点，与x轴相交于C点，的面积是.若将直线向下平移1个单位，则所得直线与双曲线的交点有(   )

A.0个 B.1个 C.2个 D.0个或1个或2个

10.如图 (1), 已知扇形AOB, 点P 从点O 出发, 沿, 以 的速度运动. 设点P 的运动时间为xs,OP 的长为 ,y随x 变化的关系图象如图 (2) 所示, 则扇形AOB 的面积为(   )

A. B. C. D.

二、填空题（本大题共5个小题，每小题3分，共15分）

11.微电子技术的不断进步，使半导体材料的精细加工尺寸大幅度缩小.某种电子元件的面积大约为0.0000007平方毫米，0.0000007用科学记数法可表示为______.

12.已知（m为任意实数），则P,Q的大小关系为________.

13.如图，在边长为4的等边中，D，E分别为，的中点，于点F，G为的中点，连接，则的长为__________.

14.如图，反比例函数和的图象在第一象限内分别交矩形的顶点C和对角线的中点D，则k的值为_________.

15.如图, 矩形ABCD中, ,, 延长BC 到点F, 使, 连接AF 交CD于点E, 连接BD, 点G,H 分别为EF,DB 的中点, 连接HG, 则HG 的长为___________.

三、解答题（本大题共8个小题，共75分.解答应写出文字说明，证明过程或演算步骤）

16.（本题共2个小题，每小题5分，共10分）

(1)计算:.

(2)化简:.

17.（8分）如图, 在四边形ABCD 中,,,.

(1)请用尺规作图法, 作 的平分线, 交AB 于点E; (保留作图痕迹, 不要求写作法)

(2)在 (1) 的条件下, 若, 求CD 的长.

18.（7分）为丰富课后服务内容，某校开设了“3D”打印、数学史、诗歌欣赏、陶艺制作四门校本课程，为了解学生对这四门校本课程的喜爱情况，对学生进行了随机问卷调查，分别用代表这四门学科，并对调查结果分析后绘制了如下两幅图不完整的统计图.

请你根据图中提供的信息完成下列问题：

（1）求被调查学生的人数？

（2）并将条形统计图补充完整；

（3）已知该校有1500名学生，估计该校学生喜爱学科C的学生有多少人？

（4）小明和小亮参加校本课程学习，若每人从三门校本课程中随机选取一门，请用画树状图或列表格的方法，求两人恰好选中同一门校本课程的概率.

19.（8分）如图（1），要在一条笔直的路边l上建一个燃气站，向l同侧的A，B两个城镇分别铺设管道输送燃气.试确定燃气站的位置，使铺设管道的路线最短.

（1）如图（2），作出点A关于l的对称点，线段与直线l的交点C的位置即为所求，即在点C处建燃气站，所得路线ACB是最短的.

为了证明点C的位置即为所求，不妨在直线l上另外任取一点，连接，，证明.请完成这个证明.

（2）如果在A，B两个城镇之间规划一个生态保护区，燃气管道不能穿过该区域.请分别给出下列两种情形的铺设管道的方案（不需说明理由）.

①生态保护区是正方形区域，位置如图（3）所示；

②生态保护区是圆形区域，位置如图（4）所示.

20.（8分）李老师在课堂上出示了这样一道问题:

如图 (1), 内接于, 分别过点B,A 作 于点 E,于点F, 过点 O作 于点M, 设AF,BE 交于点H, 求证:.

勤奋小组作辅助线的方法如下: 连接 CO并延长交 于点N, 连接AN,BN,OB.

(1)请借助勤奋小组所作辅助线证明.

(2)解决问题: 如图 (2), 在 中, ,于点 D,于点 E,AE,CD交于点F, 若, 则AF 的长为________.

21.（8分）如图是某地铁出站口扶梯侧面设计示意图, 起初工程师计划修建一段坡度为, 高度 为 32 米的扶梯AB, 但这样坡度太陡容易引发安全事故. 现工程师对设计图进行了修改: 修建AC,DE 两段扶梯, 并在这两段扶梯之间修建 5 米的水平平台CD, 其中,, 扶梯AC 长 米, 点B,E 在同一水平线上. 求修改后扶梯底部 E与原来扶梯底部B 之间的距离. (结果精确 到 0.1 米. 参考数据: ,,,)

22.（13分）综合与实践

问题情境:

在 中, , 点D 在BC 边上, 连接AD, 将AD 绕点 A逆时针旋转至AE 的位置, 使得  .

猜想证明：

(1) 如图 (1), 若, 连接CE, 试判断四边形ADCE 的形状, 并说明理由.

(2) 如图 (2), 连接BE, 取BE 的中点G, 连接AG, 请猜想线段AG 与CD 的数量关系, 并加以证明. 解决问题:

(3) 如图 (3), 若,, 连接DE 交 AC于点H, 请直接写出 的面积.

23.（13分）如图, 抛物线与x 轴交于A,B 两点 (点 A在点B 左侧), 与 y轴交于点C, 其顶点是 点D. 已知点E, 点C 关于x 轴对称, 直线EF 与x 轴交于点.

(1)求点A,B,D 的坐标及直线EF 的表达式;

(2)如图 (1), 若点P 是第一象限内抛物线上一动点, 过点 P且平行于 y轴的直线交EF 于点Q, 连接CP, 当 时, 求点P 的坐标;

(3)如图 (2), 将抛物线向右平移 个单位长度, 点D 的对应点为, 点A 的对应点为, 当 是直角三角形时, 直接写出 m的值.

答案以及解析

1.答案： B

解析：根据乘法分配律得，只有B正确，故选B．

2.答案：C

解析：解：因为左视图是侧投影面上的正投影，并存在看不见的轮廓，根据三视图的定义可得该几何体的左视图是图C.故选C.

3.答案：C

解析：A、是最简二次根式，但和不是同类二次根式，无法合并，故此选项错误；

B、，和不是同类二次根式，无法合并，故此选项错误；

C、，和是同类二次根式，可以合并，故此选项正确；

D、，和不是同类二次根式，无法合并，故此选项错误.故选C.

4.答案：C

解析：如图,，. 又 ，

5.答案：C

解析：点E的坐标为，以点O为位似中心，在原点的另一侧按的相似比将缩小，

点E的对应点的横坐标为，纵坐标为，

即，故选C.

6.答案：C

解析：由题意得：，

联立，

由①②得：，

解得，

将代入①得：，

解得，

将，代入方程得：，

解得，故选C.

7.答案：D

解析：设增加人力后平均每小时铺设xm，则原计划每天铺设，根据题意，可列方程：.故选D.

8.答案：B

解析：①甲、乙两班学生的平均成绩相等，故成绩的平均水平相同，故①正确；

②甲班的成绩的方差比乙班的大，故乙班的成绩稳定，故②不正确；

③根据中位数可得乙班的中位数大于甲班的中位数，故乙班成绩优异的人数比甲班多，故③正确；

④根据甲班的中位数为93，则④佳佳得94分将排在甲班的前20名，正确；

故选D.

9.答案：B

解析：令直线与y轴的交点为点D，过点O作于点E，过点B作轴于点F，如图所示.

令直线中，则，

即.

令直线中，则，解得，

即.

在中，，，

.

，轴，，

与都是等腰直角三角形.

又，.

，

，.

，，

点B的坐标为.

点B在双曲线上，

，

即双曲线的解析式为.

将直线向下平移1个单位得到的直线的解析式为，

将代入到中，得，

整理得

，

平移后的直线与双曲线只有1个交点.

10.答案：A

解析：由题意可知动点P 在AO 和 OB上运动 的时间相同, 均为 ，， 的长为. 设, 则 ，，.

11.答案：

解析：.

故答案为：.

12.答案：

解析：因为(m为任意实数),所以,所以.

13.答案：

解析：解：连接DE，

D、E分别是AB、BC的中点，

，.

是等边三角形，且，

，.

，，，

，.

.

G是EF的中点，

.

在中，.

故答案为.

14.答案：4

解析：解：设点，，

则点，点，点，

点D是线段的中点，

，即，

点D在反比例函数图象上，代入得：

，即，

又点C在反比例函数图象上，

代入点得：，

故答案为：4.

15.答案：

解析：如图, 连接EH 并延长交AB 于点M, 连 接MF, 易证，, 即点H 是EM 的中点. 又 点G 是EF 的中点, GH是 的中 位线,. 易得点E 是DC 的中点, 结合点H 是DB 的中点, 可知点M 是AB 的中点,.,. 在中,，.

16.答案： (1)

(2)

解析：(1) 原式

(2)原式

17.答案： (1)见解析

(2)4

解析：(1)如图, 射线CE 即为所求作的角平分线

(2) 由 (1) 知CE平分,

，

，

，

，

，

，

又，

四边形 AECD 为平行四边形

18.答案：（1）被调查学生的人数为120人

（2）图见解析

（3）估计该校学生喜爱学科C的约有225人

（4）

解析：（1）（人），

答：被调查学生的人数为120人.

（2）A学科人数为（人），

补全图形如下：

（3）（人）

答：估计该校学生喜爱学科C的约有225人.

（4）列表如下：

由列表可知：共有9种等可能的结果，其中两人恰好选中同一门校本课程的结果有3种，

所以两人恰好选中同一门校本课程的概率为.

答：两人恰好选中同一门校本课程的概率为.

19.答案：（1）证明：连接.
点A，点关于l对称，点C在l上，
，
.
同理可得.

，
.
（2）①如图（1），

在点C处建燃气站，铺设管道的最短路线是（其中D是正方形的顶点）.

②如图（2），

在点C处建燃气站，铺设管道的最短路线是（其中CD，BE都与圆相切）.

20.答案： (1)见解析

(2)

解析：(1) 证明:, ,

点M 是BC 的中点.

又 点O 是CN 的中点,.

方法一: CN 是 的直径,

，

又，，

，，

四边形  ANBH 是平行四边形"

方法二: 如图 (1), 四边形ANBC 内接于,

，

，

，

，，

又，

CN是，的直径

，即

又，

又，

(2)如图 (2), 作 的外接圆, 设圆心为O,

过点O 作 于点H, 连接OB,OC, 则.

同 (1) 可知.

，，

，

，，

21.答案：25.71

解析：如图, 分别过点A,D 作EB 的垂线, 垂足分别为点F,H, 延长DC 交AF 于点M,

则四边形DMFH 是矩形,

，，，

在中, ，

，AB的坡度为,

,

在中, ,

22.答案： (1) 四边形ADCE 是菱形，理由见解析

(2) .

(3)

解析：(1) 四边形ADCE 是菱形.

理由:，.

又 ，

，

，

，，

，

又， 四边形 ADCE是平行四边形

又 ， 四边形  ADCE是菱形

(2)证明: 方法一: 如图 (1), 延长BA 至点F, 使, 连接EF.

G是 BE的中点,.

，，

，

又，

，，

方法二: 如图 (2), 延长AG 至点M, 使, 连 接BM.

，，，

，

，，，

，

，

，

又，，

，

(3)如图 (3), 过点D 作 于点P, 过点A 作 于点Q.

，，

，

是等边三角形

，

，

，

，

，

又，

，

，，

，，

即，，

，

23.答案： (1)

(2) 或

(3)或 7

解析： (1)对于, 令, 解得，, 故，.

,

点D 的坐标为.

易知,

点E, 点C 关于x 轴对称,

点E 的坐标为.

设直线EF 的表达式为,

将 ，分别代入,

可得  解得

故直线 EF的表达式为.

(2)设点P的坐标为, 则 点Q 的坐标为.

过点P 作 轴, 垂足为点M, 过点Q 作 轴,垂足为点N.

轴， 又，

，

当 时, 如图 (1), 易得, 则四边形CEQP 是平行四边形,

，

(舍去)

点 P的坐标为

当 时, 如图 (2), 易得四边形MNQP 是矩形.

，

(舍去)，，

点  P的坐标为

综上所述, 点P 的坐标为 或.

 (3)易知 是锐角, 故分 和 两种情况讨论即可.

易知，.

当 时, 如图 (3), 过点 作 轴于 点G, 则,

即，

当 时, 如图 (4), 过点 作 轴于 点H, 则, , 即,

(负值不合题意,已舍去).

故m 的值为 2 或 7 .