小升初真题汇编应用题（三）-2023年六年级下册数学高频考点苏教版（江苏徐州）

这是一份小升初真题汇编应用题（三）-2023年六年级下册数学高频考点苏教版（江苏徐州），共21页。试卷主要包含了如图等内容，欢迎下载使用。

小升初真题汇编应用题（三）
2023年六年级下册数学高频考点苏教版（江苏徐州）
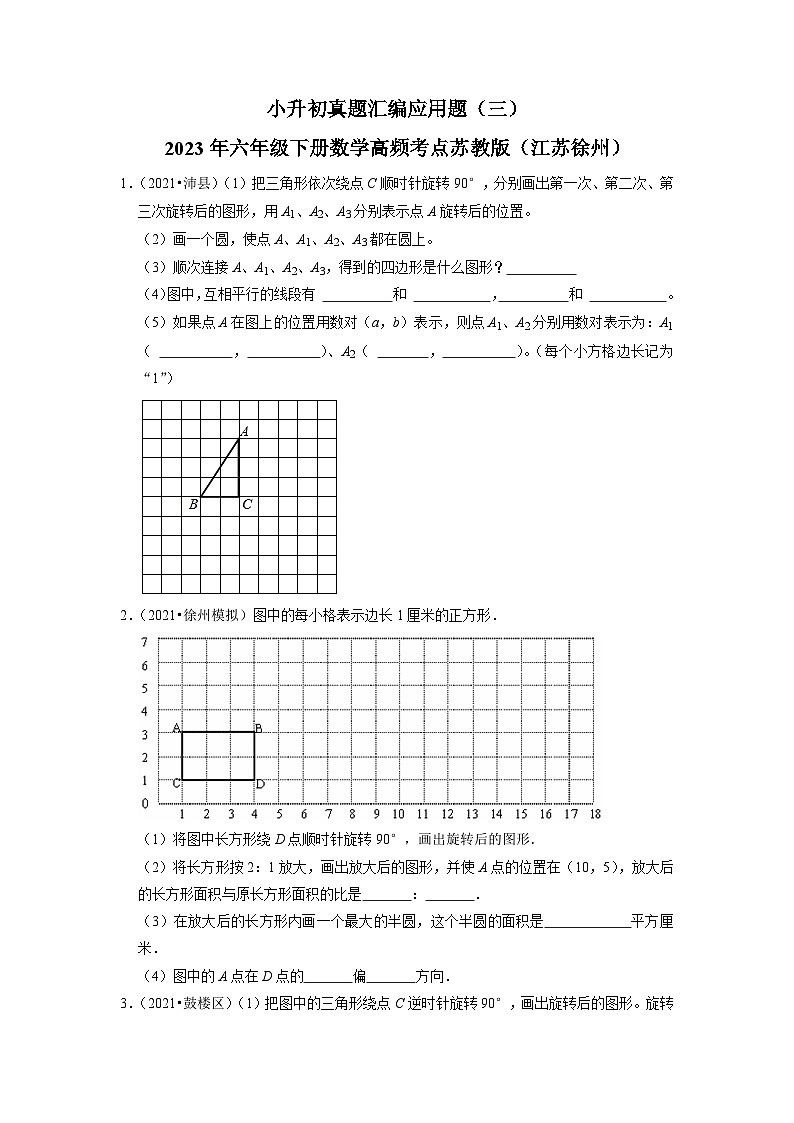
1．（2021•沛县）（1）把三角形依次绕点C顺时针旋转90°，分别画出第一次、第二次、第三次旋转后的图形，用A1、A2、A3分别表示点A旋转后的位置。
（2）画一个圆，使点A、A1、A2、A3都在圆上。
（3）顺次连接A、A1、A2、A3，得到的四边形是什么图形？　 　
（4）图中，互相平行的线段有 　 　和 　 　，　 　和 　 　。
（5）如果点A在图上的位置用数对（a，b）表示，则点A1、A2分别用数对表示为：A1（ 　 　，　 　）、A2（ 　 　，　 　）。（每个小方格边长记为“1”）

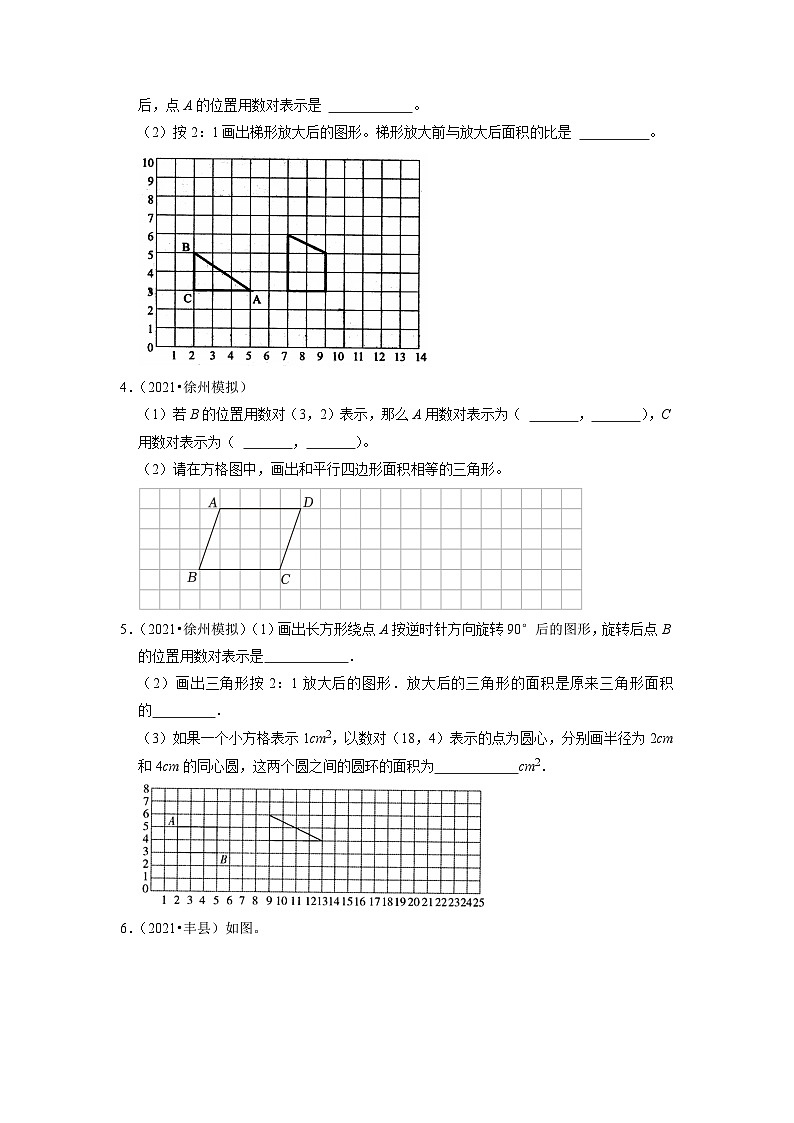
2．（2021•徐州模拟）图中的每小格表示边长1厘米的正方形．

（1）将图中长方形绕D点顺时针旋转90°，画出旋转后的图形．
（2）将长方形按2：1放大，画出放大后的图形，并使A点的位置在（10，5），放大后的长方形面积与原长方形面积的比是　 　：　 　．
（3）在放大后的长方形内画一个最大的半圆，这个半圆的面积是　 　平方厘米．
（4）图中的A点在D点的　 　偏　 　方向．
3．（2021•鼓楼区）（1）把图中的三角形绕点C逆时针旋转90°，画出旋转后的图形。旋转后，点A的位置用数对表示是 　 　。
（2）按2：1画出梯形放大后的图形。梯形放大前与放大后面积的比是 　 　。

4．（2021•徐州模拟）
（1）若B的位置用数对（3，2）表示，那么A用数对表示为（ 　 　，　 　），C用数对表示为（ 　 　，　 　）。
（2）请在方格图中，画出和平行四边形面积相等的三角形。

5．（2021•徐州模拟）（1）画出长方形绕点A按逆时针方向旋转90°后的图形，旋转后点B的位置用数对表示是　 　．
（2）画出三角形按2：1放大后的图形．放大后的三角形的面积是原来三角形面积的　 　．
（3）如果一个小方格表示1cm2，以数对（18，4）表示的点为圆心，分别画半径为2cm和4cm的同心圆，这两个圆之间的圆环的面积为　 　cm2．

6．（2021•丰县）如图。

①小军家在学校的 　 　偏 　 　　 　°的方向上，距离约是 　 　m。
②小红家距离学校200m，请在图中画出小红家的所有可能位置。
7．（2020•徐州）
（1）将三角形ABC绕C点顺时针旋转90°，画出旋转后的图形．
（2）将旋转后的图形向上平移3格，画出平移后的图形；平移后C点的位置用数对表示是（　 　，　 　）．
（3）以点O为圆心，按2：1画出圆形放大后的图形．
（4）图中三角形MNP是一个等边三角形，那么点P在点M的　 　偏　 　°方向　 　厘米处．
8．（2021•南通）（1）下图中的左上角已经涂出3个方格，请再涂一个方格，使这4个方格组成一个轴对称图形，并画出它的对称轴。
（2）三角形ABC中，点A的位置用数对表示是（ 　 　，　 　）；点A在点C的 　 　偏 　 　　 　度方向。
（3）将三角形ABC绕A点逆时针旋转90°。
（4）过O点画一条线段，把正方形分成一个三角形和一个梯形，使三角形与梯形的面积比为3：5。
9．（2022•徐州）如图，玲玲一开始站在小树的位置，她向东走用正数表示，向西走用负数表示。她先走了+2米，又走了﹣7米，最后走了+3米。请你在图中用△标出她现在的位置。（每两点之间的距离是1米）

10．（2022•徐州）一条生产线每3分钟自动记录一次生产产品的总数量，下面是生产产品情况的记录。
时间/分
3
6
9
12
……
产品数量/个
51
102
153
204
……
（1）生产产品的时间和产品数量成 　 　比例。
（2）照这样计算，45分钟生产产品多少个？
11．（2022•徐州）一种药品的包装盒上印有下面一段话，请你仔细阅读，解决以下问题：
【药品名称】阿英西林分散片
【成份】主要成份为阿莫西林
【性状】白色或类白色片
【适应症】抗生素，其抗菌谱与氨苄青霉素相同，对敏感的革兰氏阳性球菌和杆菌及革兰氏阴性菌均有明显的抑制作用。适用于敏感菌所致呼吸道感染、尿路感染、胃肠道感染、败血症、皮肤及软组织感染等症。
【用法用量】口服：成人一次0.5～1g，一日3～4次；小儿每日按体重50～100mg/kg，分3～4次服用。
【禁忌】对青霉素过敏者禁用
【规格】0.25g/片
【包装规格】0.25g×24片/盒
注：字母mg表示质量单位毫克。1g＝1000mg
（1）这盒药最多可供成人服用几次？
（2）这盒药够体重为20kg的儿童服用三天吗？
12．（2021•沛县）甲、乙两人买水果，甲习惯买一定重量的水果，乙习惯买一定金额的水果，两人每次买水果的单价相同，例如：
第一次：

西瓜6元/千克
重量
金额
甲
5千克
30元
乙
5千克
30元
第二次：

西瓜4元/千克
重量
金额
甲
5千克
　 　元
乙
　 　千克
30元
（1）完成上表；
（2）计算甲两次买水果的均价和乙两次买水果的均价。（均价＝总金额÷总重量）
13．（2021•沛县）王师傅准备用一块长方形铁皮制作一个无盖的水箱，他在铁皮上画了一个水箱的平面展开图（如图1）。
（1）王师傅设计的这个水箱容积是多少升？（铁皮厚度忽略不计）
（2）若在水箱下方焊接一个水管，水管的内直径是20毫米。放水时，如果水流的速度是0.7米/秒，一箱水大约多少分钟可以全部流完？（结果保留整数）
（3）王师傅发现这样设计，剩余的铁皮太零碎。你能在不改变水箱尺寸和底面形状的情况下，帮王师傅重新设计一个水箱平面展开图吗？请将你的想法画在图2中。

14．（2022•徐州）（1）请在图中选择四个点，依次连接，围成一个平行四边形。

（2）选择图中的三个点，依次连接，能画出 　 　个等腰三角形。
（3）画出其中一个等腰三角形，并画出它向右平移3格后的图形。
（4）若所画等腰三角形一个顶点的位置用数对（a，b）表示，则它平移后的位置用数对（ 　 　，　 　）表示。
15．（2022•徐州）刘老师家的厨房，长3.2米，宽2.4米。刘老师在装修厨房时，看中了三种地砖，它们的尺寸与价格分别如下：
A款：80×80cm，每块150元；
B款：60×60cm，每块80元；
C款：40×40cm，每块40元。
如果想省钱（在铺地砖时，可以切割），你建议刘老师选哪一款？为什么？（如果思考有困难，可以先在草图上画一画，再解答）

16．（2022•徐州）（1）如图表示李梅0～25岁身高与年龄的变化情况。25岁以前，她有两个生长高峰期，分别是 　 　。
A.0～5岁，5～10岁
B、5～10岁，15～20岁
C.10～15岁，20～25岁
D.0～5岁，10～15岁
（2）0～5岁期间，李梅身高平均每年增长 　 　厘米。
（3）如果用h表示李梅的身高，用a表示她10～15岁平均每年增长的厘米数，那么她13岁时的身高用含有字母的式子表示为h＝　 　厘米。

17．（2020•徐州）少先队员参加植树活动，六年级植树的棵数是五年级的1.5倍，五年级比六年级少植树24棵，两个年级各植树多少棵？
18．（2021•丰县）西山果园原有36行苹果树，每行的棵数相等，今年打算再栽这样的15行，需要购进苹果树苗675棵，西山果园原有苹果树多少棵？
19．（2020•三明）参加数学兴趣小组的同学中，五年级比四年级的3倍少35人，两个年级的人数差是41人，两个年级参加数学兴趣小组的各有多少人？

小升初真题汇编应用题（三）
2023年六年级下册数学高频考点苏教版（江苏徐州）
参考答案与试题解析
一．操作题（共8小题）
1．【答案】（1）（2）如图：

（3）如图，正方形；
（4）AA1、A3A2，AA3、A1A2；（答案不唯一）
（5）a+3，b﹣3，a，b﹣6。
【分析】（1）根据旋转的特征，把图形各顶点绕C点顺时针旋转90°，顺次连接即可得到第一次旋转后的图形；将第一次得到的图形各顶点绕C点顺时针旋转90°，顺次连接即可得到第二次旋转后的图形；将第二次得到的图形各顶点绕C点顺时针旋转90°，顺次连接即可得到第三次旋转后的图形；依欠标记A点的对应点为：A1、A2、A3；
（2）以C点为圆点，画一个半径为3格的圆；
（3）顺次连接A、A1、A2、A3，即可得到一个正方形；
（4）根据平行线的特征判断即可；
（5）用数对表示位置时，前一个数表示列，后一个数表示行，向右平移几格，列数加几，向左平移几格，列数减几，向上平移几格，行数加几，向下平移几格，行数减几；据此解答。
【解答】解：（1）（2）作图如下：

（3）如图，顺次连接A、A1、A2、A3，即可得到一个正方形；
（4）图中，互相平行的线段有AA1和A3A2，AA3和A1A2；（答案不唯一）
（5）如果点A在图上的位置用数对（a，b）表示，则点A1、A2分别用数对表示为：A1（a+3，b﹣3）、A2（a，b﹣6）。
故答案为：正方形；AA1，A3A2，AA3，A1A2（答案不唯一）；a+3，b﹣3，a，b﹣6。
【点评】本题主要考查了图形的旋转、平行、数对知识点；图形的旋转不改变图形的形状和大小，只改变图形的位置；用数对表示位置时，前一个数表示列，后一个数表示行。
2．【答案】见试题解答内容
【分析】（1）根据旋转的特征，长方形绕点D顺时针旋转90°，点D的位置不动，其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形．
（2）根据图形放大与缩小的意义，把这个长方形的长、宽均放大到原来的2倍，并让点A在（10，5）的位置（根据用数对表示点的位置的方法，第一个数字表示列数，第二个数字表示行数）；把放大后与原长方形的比的前、后项分别平方就是放大后的长方形面积与原长方形面积的比．
（3）在放大后的长方形内所画的最大半圆的半径是放大后长方形长的一半，计算出圆的面积除以2．
（4）根据平面图上的方向，上北下南，左西右东，以点D为观测点即可确定点A的方向．
【解答】（1）将图中长方形绕D点顺时针旋转90°，画出旋转后的图形（图中红色部分）：
（2）将长方形按2：1放大，画出放大后的图形，并使A点的位置在（10，5）（图中绿色部分），放大后的长方形面积与原长方形面积的比是4：1．
（3）在放大后的长方形内画一个最大的半圆（图中蓝色部分），这个半圆的面积是：
3.14×32÷2
＝28.26÷2
＝14.13（平方厘米）
（4）图中的A点在D点的西偏北方向．

故答案为：4，1；14.13；西，北．
【点评】此题考查的知识有：数值与位置、作旋转一定度数后的图形、图形的放大与缩小、圆（半圆）面积的计算、长方形面积的计算、比的意义、根据方向和距离确定物体的位置等．
3．【答案】；（2，6）；1：4。
【分析】（1）根据旋转的特征，图中三角形ABC绕点C逆时针旋转90°，点C的位置不动，其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形；根据用数对表示点的位置的方法，第一个数字表示列数，第二个数字表示行数及旋转后点A所在列、行，即可用数对表示出它的位置。
（2）根据图形放大与缩小的意义，把这个直角梯形的上、下底及高均放大到原来的2倍，对应角大小不变，所得到的图形就是原图形按2：1放大后的图形。根据梯形的面积计算公式“S＝（a+b）h÷2”，分别求出放大前、后的面积，再根据比的意义即可写出放大前与放大后面积的比，并化成最简整数比。
【解答】解：（1）把图中的三角形绕点C逆时针旋转90°，画出旋转后的图形（图中红色部分）。旋转后，点A的位置用数对表示是（2，6）。
（2）按2：1画出梯形放大后的图形（图中绿色部分。梯形放大前与放大后面积的比是：
[（2+3）×2÷2]：[（4+6）×4÷2]
＝[5×2÷2]：[10×4÷2]
＝5：20
＝1：4

故答案为：（2，6）；1：4。
【点评】此题考查的知识点：作旋转一定度数后的图形、数对与位置、图形的放大与缩小、比的意义及化简、梯形面积的计算等。
4．【答案】（1）4，5，7，2。
（2）


【分析】（1）由“点B用数对（3，2）表示”可知，数对第一个数字表示列，第二个数字表示行．据此即可用数对分别表示出点B、C的位置．一个图形的各顶点分别向左、右平移几格后，行数不变，列数减（或加）几；据此解答。
（2）根据平行四边形的面积公式S＝ah，求出平行四边形的面积，再据此画出三角形。（面积相等即可，形状不唯一）
【解答】解：（1）若B的位置用数对（3，2）表示，那么A用数对表示为（4，5），C用数对表示为（7，2）。
（2）假设图上每个小方格的边长为1cm，则平行四边形的底为4cm，高为3cm。
平行四边形的面积为：4×3＝12（cm2）
所以三角形的面积为12cm2，三角形在方格纸上如下所示：

故答案为：4，5，7，2。

【点评】此题主要考查了坐标与图形变化﹣平移，熟练掌握点的坐标变化规律是解题关键。
5．【答案】见试题解答内容
【分析】（1）根据旋转的特征，长方形绕点A逆时针旋转90°，点A的位置不动，其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形．根据用数对表示点的位置的方法，第一个数字表示列数，第二个数字表示行数，即可用数对表示出旋转后点B的位置．
（2）根据图形放大与缩小的意义，把这个三角形的两直角边均放大到原来的2倍，所得到的图形就是原图形按2：1放大后的图形；根据三角形面积计算公式“S＝ah÷2”分别求出放大后三角形的面积、原三角形的面积，用放大后三角形的面积除以原三角形的面积．
（3）圆心的位置、半径已知，据此即可画出这两个同心圆；根据环形面积计算公式“S＝π（R2﹣r2）”即可求出环形面积．
【解答】解：（1）画出长方形绕点A按逆时针方向旋转90°后的图形（图中红色），旋转后点B的位置用数对表示是（4，8）．
（2）画出三角形按2：1放大后的图形（图中绿色）．放大后的三角形的面积是原来三角形面积的：
（8×4÷2）÷（4×2÷2）
＝16÷4
＝4倍．

（3）如果一个小方格表示1cm2，以数对（18，4）表示的点为圆心，分别画半径为2cm和4cm的同心圆（图中蓝色），这两个圆之间的圆环的面积为：
3.14×（42﹣22）
＝3.14×（16﹣4）
＝3.14×12
＝37.68 （cm2）．

故答案为：（4，8），4倍，37.68．
【点评】此题考查的知识较多：作旋转后的图形、数对与位置、图形的放大与缩小、三角形面积的计算、画圆、环形面积的计算等．
6．【答案】①北，东，45，400；
②

【分析】①以学校为观测点，小军家、学校的连线在正北方与正东方之间，与正北方的夹角为45°，小军家与学校相距4个100米；
②小红家距离学校200米，小红家所有可能位置在以学校为圆心，半径为200米的圆上。
【解答】解：①小军家在学校的北偏东45°的方向上，距离约是400m；
②

故答案为：北，东，45，400。
【点评】此题重点考查如何以方向和距离确定物体位置以及圆上每一点到圆心的距离都相等。
7．【答案】
3，4；北（或）东，东（或北）60（或30），3．
【分析】（1）根据旋转的特征，三角形ABC绕点C顺时针旋转90°，点C的位置不动，其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形．
（2）根据平移的特征，把旋转后的三角形的各顶点分别向上平移3格，依次连接即可得到向上平移3格后的图形；根据用数对表示点的位置的方法，第一个数字表示列数，第二个数字表示行数，即可用数对表示出平移后点C的位置．
（3）这个圆的半径是1格，根据图形放大与缩小的意义，按2：1放大后的圆的半径是2格，据此即可画出按2：1放大后的圆．
（4）等边三角形的每个角都是60°，根据平面图形上方向的辨别“上北下南，左西右东”，以点M的位置为观测点即可确定点P的方向，MP＝MN＝3厘米．
【解答】解：（1）将三角形ABC绕C点顺时针旋转90°，画出旋转后的图形（图中红色部分）．
（2）将旋转后的图形向上平移3格，画出平移后的图形（图中绿色部分）；平移后C点的位置用数对表示是（3，4）．
（3）以点O为圆心，按2：1画出圆形放大后的图形（图中蓝色部分）．
（4）图中三角形MNP是一个等边三角形，那么点P在点M的北（或东）偏东（或北）30（或60）°方向3厘米处．

故答案为：3，4；北（或东），东（或北）30（或60），3．
【点评】此题考查的知识点较多：作旋转一定度数后的图形、作平移后的图形、图形的放大与缩小、画圆、数对与位置、根据方向和距离确定物体的位置等．
8．【答案】（1）、（3）、（4）（第一小题画法不唯一）；（2）（6，4），西，北，45。
【分析】（1）涂法不唯一。可在行的右边再涂一个方格，这四个涂色方格即可组成一个轴对称图形。过中间一列正方形中间的纵向直线就是它的对称轴。
（2）根据用数对表示点的位置的方法，第一个数字表示列数，第二个数字表示行数，即可用数对表示出点A的位置；这个三角形是等腰直角三角形，每个锐角都是45°，再根据平面图上方向的辨别“上北下南，左西右东”，以点C的位置为观测点，即可确定点A的方向。
（3）根据旋转的特征，三角形ABC绕点A逆时针旋转90°，点A的位置不动，这个三角形的各边均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
（4）把这个正方形的上、下边所占的格数之和平均分成（3+5）份，三角形的底占3份，底形的上、下底之和占5份，这样分成的三角形与梯形等高，根据三角形的面积计算公式“S＝ah÷2”、梯形的面积计算公式“S＝（a+b）h÷2”可知，三角形的面积与梯形面积的比是3：5。
【解答】解：（1）下图中的左上角已经涂出3个方格，请再涂一个方格，使这4个方格组成一个轴对称图形，并画出它的对称轴（下图、画法不唯一）。
（2）三角形ABC中，点A的位置用数对表示是（6，4）；点A在点C的西偏北45度方向。
（3）将三角形ABC绕A点逆时针旋转90°（下图）。
（4）过O点画一条线段，把正方形分成一个三角形和一个梯形，使三角形与梯形的面积比为3：5（下图）。

故答案为：（6，4），西，北，45。
【点评】此题考查的知识点：数对与位置、作旋转一定度数后的图形、三角形面积各的计算、梯形面积各的计算、比的应用、根据方向确定物体的位置等。
二．解答题（共11小题）
9．【答案】
【分析】用正负数表示意义相反的两种量：向东走用正数表示，向西走用负数表示。把所有数据相加，求出最后的数，再根据正负号和数字判断位置即可。
【解答】解：+2﹣7+3＝﹣2（米）

【点评】此题主要考查正负数的意义，正数与负数表示意义相反的两种量，看清规定哪一个为正，则和它意义相反的就为负。
10．【答案】（1）正；
（2）765个。
【分析】两个相关联的量，若两个量的比值一定，两个量成正比例关系；若两个量的乘积一定，两个量成反比例关系，据此判断即可。
【解答】解：（1）51：3＝102：6＝153：9＝204：12＝17
答：生产产品的时间和产品数量成正比例。
（2）17×45＝765（个）
答：45分钟生产产品765个。
故答案为：正。
【点评】根据正比例的判断方法，解答此题即可。
11．【答案】（1）12次；（2）够。
【分析】（1）每片0.25克，一盒有24片，用24乘0.25求出这盒药一共有多少克，成人一次0.5～1g，最小剂量是0.5克，用这盒药的总剂量除以0.5克即可求出这盒药最多可供成人服用几次；
（2）小儿每日按体重50～100mg/kg，20千克体重的儿童最小剂量为50×20＝1000（毫克），然后再用这盒药的总剂量除以20千克儿童每天的最小剂量求出一共可以服几天，然后再和三天进行比较即可判断。
【解答】解：（1）24×0.25＝6（克）
6÷0.5＝12（次）
答：这盒药最多可供成人服用12次；

（2）6克＝6000毫克
6000÷（50×20）
＝6000÷1000
＝6（天）
6＞3，所以够体重为20kg的儿童服用三天。
答：够体重为20kg的儿童服用三天。
【点评】本题主要考查了小数乘除法的意义和实际应用，要熟练掌握，注意单位换算。
12．【答案】（1）

西瓜4元/千克
重量
金额
甲
5千克
20元
乙
7.5千克
30元
（2）甲两次买水果的均价为5元/千克，乙两次买水果的均价为4.8元/千克。
【分析】能根据表格中提供的信息进行数量分析，金额＝重量×单价，重量＝金额÷单价。据此解答。
【解答】解：（1）5×4＝20（元）
30÷4＝7.5（千克）

西瓜4元/千克
重量
金额
甲
5千克
20元
乙
7.5千克
30元
（2）甲：（20+30）÷（5+5）
＝50÷10
＝5（元/千克）
乙：（30+30）÷（5+7.5）
＝60÷12.5
＝4.8（元/千克）
答：甲两次买水果的均价为5元/千克，乙两次买水果的均价为4.8元/千克。
【点评】知道金额＝重量×单价，重量＝金额÷单价这两个公式是解本题的关键。
13．【答案】（1）24升，（2）2分钟；（3）答案不唯一。
【分析】（1）这个长方体水箱的长是40厘米，宽是20厘米，高是30厘米，长×宽×高求出这个水箱容积；
（2）水在自来水管内的形状是圆柱形，可利用圆柱的体积公式V＝Sh先求出每秒水流的体积，再乘60求出每分水流的体积，再用水箱中水的体积除以每分水流的体积求出流完的时间；
（3）根据长方体展开图的特点解答，答案不唯一。
【解答】解：（1）40×20×30
＝800×30
＝24000（立方厘米）
24000立方厘米＝24升
答：王师傅设计的这个水箱容积是24升。
（2）20毫米＝2厘米
0.7米＝70厘米
3.14×（2+2）2×70
＝3.14×70
＝219.8（立方厘米）
24000÷（219.8×60）
＝24000÷13188
≈2（分钟）
答：一箱水大约2分钟可以全部流完。
（3）如图：
答案不唯一
【点评】考查了长方体的容积、圆柱的体积、长方体展开图的灵活应用，计算时要认真。
14．【答案】见试题解答内容
【分析】（1）结合题意，选择A、B、D、E四个点连接即可画出平行四边形。
（2）根据等腰三角形的特点，选择图中的三个点，依次连接，能画出三角形ABE、三角形ADE、三角形DEF等3个等腰三角形。
（3）根据平移的方法，画出其中一个等腰三角形DEF，然后向右平移3格后画出即可。
（4）根据数对知识和用字母表示数的知识解答即可。
【解答】解：（1）选择四个点，依次连接，围成一个平行四边形（如图）。

（2）选择图中的三个点，依次连接，能画出三角形ABE、三角形ADE、三角形DEF等3个等腰三角形。
（3）画出其中一个等腰三角形DEF，画出它向右平移3格后的图形（如图）。
（4）若所画等腰三角形一个顶点的位置用数对（a，b）表示，则它平移后的位置用数对（a+3，b）表示。
故答案为：（2）3；（4）a+3，b。
【点评】本题考查了平行四边形、等腰三角形、平移及数对等知识，结合题意解答即可。
15．【答案】B。
【分析】要满铺厨房地面，地面为长方形，地砖为正方形，就用正方形的边长分别来平分长方形的宽和长。
用A款80×80cm的需要4×3块；用B款的需要5×4+2块；用C款的需要8×6块；然后求出总价，对比作选择。
【解答】解：2.4m＝240cm 3.2m＝320cm
240÷80＝3（块） 320÷80＝4（块） 3×4＝12 （块） 150×12＝1800（元）
240÷60＝4（块） 320÷60＝5（块）……20（cm）
20×240＝4800（cm2）
4800÷（60×60）
＝4800÷3600
＝1……1200（cm2）
1+1＝2（块） 4×5+2＝22（块）
80×22＝1760（元）
240÷40＝6（块） 320÷40＝8（块） 6×8＝48（块）
40×48＝1920（元）
1920＞1800＞1760
答：我建议刘老师选B款。因为B款用钱少。
故答案为：B。
【点评】本题考查了学生对满铺的理解，及用数学于生活中的意识。
16．【答案】（1）D；（2）12.4；（3）（131+3a）。
【分析】（1）观察统计图，然后找出25岁以前的两个生长高峰期即可；
（2）用0～5岁期间，李梅的身高差除以5，即可求出身高平均每年增长多少厘米；
（3）根据用字母表示数的知识，结合题意解答即可。
【解答】解：（1）如图表示李梅0～25岁身高与年龄的变化情况。25岁以前，她有两个生长高峰期，分别是0～5岁，10～15岁，所以选择D。
（2）（110﹣48）÷5
＝62÷5
＝12.4（厘米）
答：0～5岁期间，李梅身高平均每年增长12.4厘米。
（3）如果用h表示李梅的身高，用a表示她10～15岁平均每年增长的厘米数，那么她13岁时的身高用含有字母的式子表示为h＝（131+3a）厘米。
故答案为：（1）D；（2）12.4；（3）（131+3a）。
【点评】本题考查了折线统计图、字母表示数等知识，结合题意分析解答即可。
17．【答案】见试题解答内容
【分析】把五年级植树的棵数看作1倍数，六年级植树的棵数是五年级的1.5倍，六年级植树的棵数比五年级植树的棵数多（1.5﹣1）倍，又知五年级比六年级少植树24棵，用除法即可得五年级植树的棵数，再求六年级植树的棵数即可．
【解答】解：24÷（1.5﹣1）
＝24÷0.5
＝48（棵）
48+24＝72（棵）
答：五年级植树48棵，六年级植树72棵．
【点评】本题考查了差倍问题，关键是得出六年级植树的棵数比五年级植树的棵数多（1.5﹣1）倍．
18．【答案】见试题解答内容
【分析】栽15行需要购进苹果树苗675棵，根据除法的意义，那么每行有675÷15＝45棵，36行共有36个45，即45×36．
【解答】解：675÷15×36
＝45×36
＝1620（棵）．
答：西山果园原有苹果树1620棵．
【点评】本题关键是求出每一行的棵数，然后再进一步解答．
19．【答案】见试题解答内容
【分析】设四年级参加数学兴趣小组的有x人，则五年级有（3x﹣35）人，根据等量关系：五年级参加数学兴趣小组的人数﹣四年级参加数学兴趣小组的人数＝41人，列方程解答即可得四年级参加数学兴趣小组的人数，再求五年级的即可．
【解答】解：设四年级参加数学兴趣小组的有x人，则五年级有（3x﹣35）人，
3x﹣35﹣x＝41
2x＝76
x＝38
38+41＝79（人）
答：四年级参加数学兴趣小组的有38人，五年级参加数学兴趣小组的有79人．
【点评】本题考查了差倍问题，关键是根据等量关系：五年级参加数学兴趣小组的人数﹣四年级参加数学兴趣小组的人数＝41人，列方程．
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2023/5/8 20:47:56；用户：李家祯；邮箱：hfnxxx59@qq.com；学号：47467572