




初中数学沪科版八年级上册14.2 三角形全等的判定一等奖ppt课件
展开1.掌握证明三角形全等的方法:SSS. (重点)
证明三角形全等的方法还有哪些?
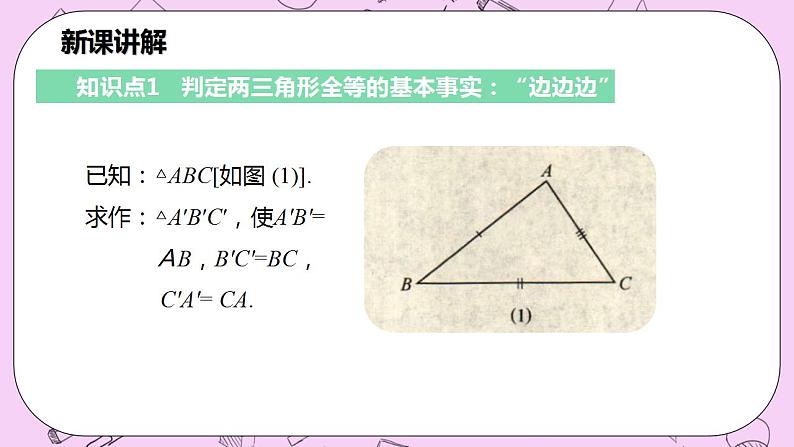
知识点1 判定两三角形全等的基本事实:“边边边”
已知:△ABC[如图 (1)].求作:△A′B′C′,使A′B′= AB,B′C′=BC, C′A′= CA.
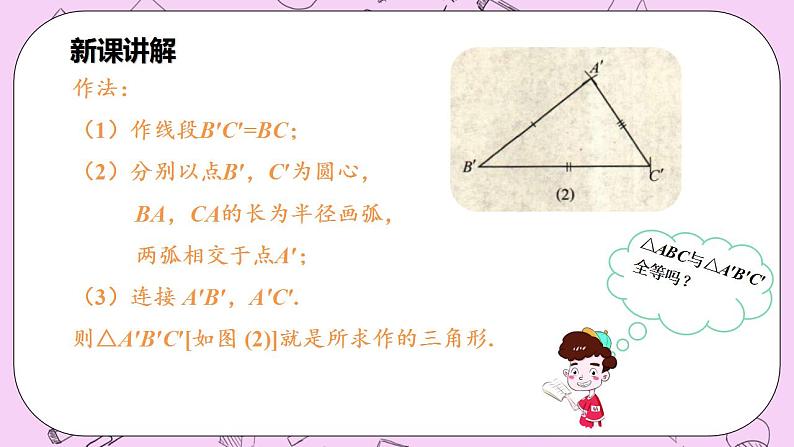
△ABC与△A′B′C′全等吗?
作法:(1)作线段B′C′=BC;(2)分别以点B′,C′为圆心, BA,CA的长为半径画弧, 两弧相交于点A′;(3)连接 A′B′,A′C′.则△A′B′C′[如图 (2)]就是所求作的三角形.
1.判定方法三:三边分别相等的两个三角形全等(简记为“边边边”或“SSS”).2.证明书写格式:在△ABC和△A′B′C′中, ∵ ∴△ABC≌△A′B′C′.
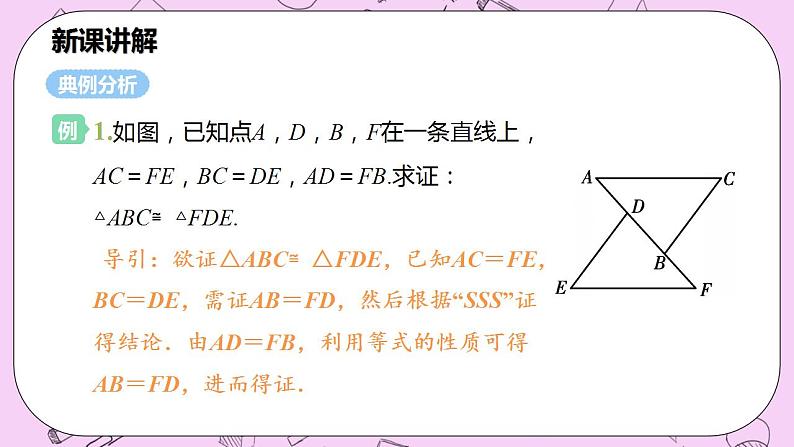
1.如图,已知点A,D,B,F在一条直线上,AC=FE,BC=DE,AD=FB.求证:△ABC≌△FDE. 导引:欲证△ABC≌△FDE,已知AC=FE,BC=DE,需证AB=FD,然后根据“SSS”证得结论.由AD=FB,利用等式的性质可得AB=FD,进而得证.
证明:∵AD=FB, ∴AD+DB=FB+DB,即AB=FD. 在△ABC与△FDE中, ∴△ABC≌△FDE(SSS).
知识点2 三角形的稳定性
四边形和三角形谁稳定?
只要三角形三边的长度确定了,这个三角形的形状和大小就完全确定,这个性质叫做三角形的稳定性.
2.王师傅用4根木条钉成一个四边形木架,如图.要使这个木架不变形,他至少还要再钉上( )根木条. A.0 B.1 C.2 D.3
1.已知:如图,AB=AC,AD=AE,BD=CE.求证:∠BAC=∠DAE.
证明:在△ABD和△ACE中, ∴△ABD≌△ACE(SSS). ∴∠BAD=∠CAE. ∴∠BAD+∠DAC=∠CAE+∠DAC, 即∠BAC=∠DAE.
2.如图,在四边形ABCD中,AB=AD,CB=CD.求证:∠B=∠D. 导引:在图中没有三角形,只有连接AC,将∠B和 ∠D分别放在两个三角形中,通过证明两个 三角形全等来证明∠B和∠D相等.
证明:如图,连接AC, 在△ABC和△ADC中, ∵AB=AD,CB=CD,AC=AC, ∴△ABC≌△ADC(SSS). ∴∠B=∠D.
3.如图,下列三角形中,与△ABC全等的是( )
4.下列图形具有稳定性的是( ) A.正方形 B.矩形 C.平行四边形 D.直角三角形5.下列图形中,不具有稳定性的是( )
沪科版八年级上册14.2 三角形全等的判定评优课课件ppt: 这是一份沪科版八年级上册14.2 三角形全等的判定评优课课件ppt,共13页。PPT课件主要包含了CONTENTS,学习目标,新课导入,新课讲解,课堂小结,当堂小练,拓展与延伸,布置作业等内容,欢迎下载使用。
初中数学沪科版八年级上册第14章 全等三角形14.2 三角形全等的判定公开课课件ppt: 这是一份初中数学沪科版八年级上册第14章 全等三角形14.2 三角形全等的判定公开课课件ppt,共13页。PPT课件主要包含了CONTENTS,学习目标,新课导入,新课讲解,课堂小结,当堂小练,拓展与延伸,布置作业等内容,欢迎下载使用。
沪科版八年级上册第14章 全等三角形14.2 三角形全等的判定习题课件ppt: 这是一份沪科版八年级上册第14章 全等三角形14.2 三角形全等的判定习题课件ppt,共25页。PPT课件主要包含了AC∥DF,△ABE≌△ACE,AB=CD等内容,欢迎下载使用。













