




还剩17页未读,
继续阅读
所属成套资源:沪科版初中数学八年级上册课件PPT
成套系列资料,整套一键下载
- 14.2.3《三边分别相等的两个三角形(SSS) 》课件 课件 19 次下载
- 14.2.4《其他判定两个三角形全等的条件》课件 课件 19 次下载
- 14.2.5《两个直角三角形全等的判定》课件 课件 19 次下载
- 14.2.6《全等三角形的判定方法的综合运用》课件 课件 23 次下载
- 第14章 《小结与复习》课件 课件 17 次下载
14.2.2《两角及其夹边分别相等的两个三角形(ASA)》课件
展开
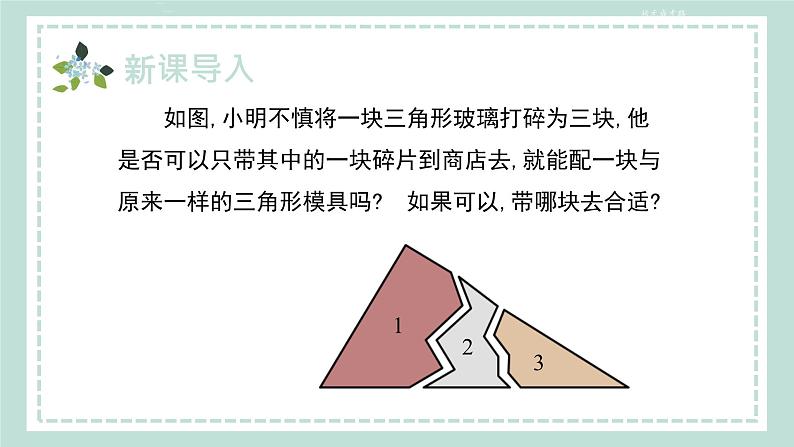
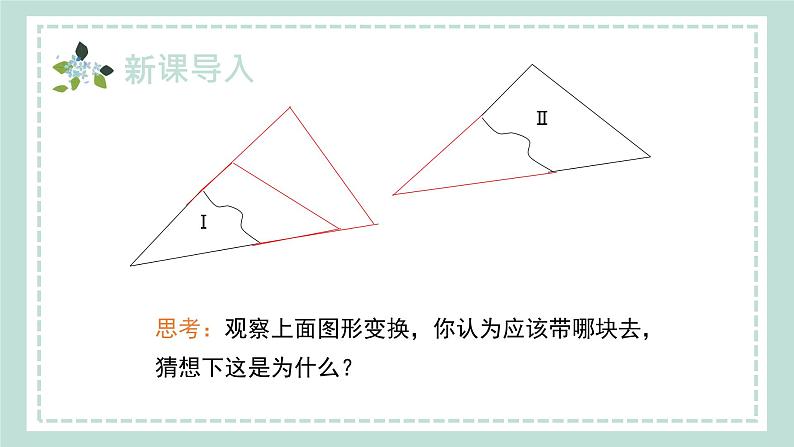
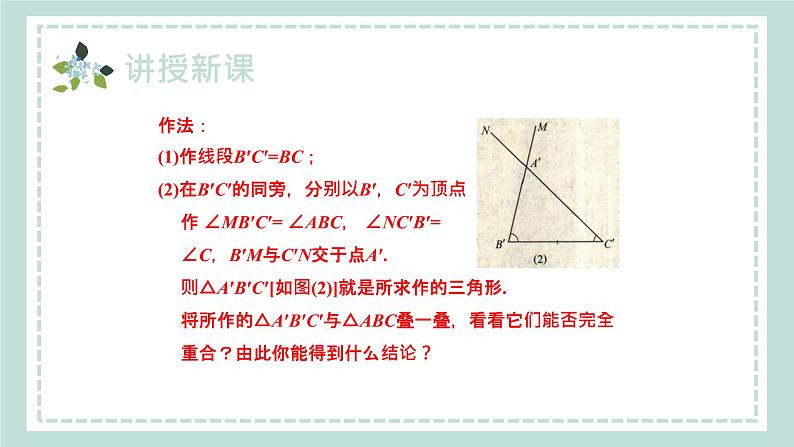
沪科版数学八年级上册14.2.2 两角及其夹边分别相等的两个三角形(ASA)新课导入讲授新课当堂练习课堂小结目录新课导入 如图,小明不慎将一块三角形玻璃打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗? 如果可以,带哪块去合适?思考:观察上面图形变换,你认为应该带哪块去,猜想下这是为什么?讲授新课 “角边角”判定方法已知:△ABC[如图 (1)].求作:△A′B′C′,使∠B′= ∠ B,B′C′=BC, ∠C′= ∠ C. 作法:(1)作线段B′C′=BC;(2)在B′C′的同旁,分别以B′,C′为顶点 作 ∠MB′C′= ∠ABC, ∠NC′B′= ∠C,B′M与C′N交于点A′. 则△A′B′C′[如图(2)]就是所求作的三角形. 将所作的△A′B′C′与△ABC叠一叠,看看它们能否完全 重合?由此你能得到什么结论?归 纳判定两个三角形全等的第2种方法是如下的基本事实. 两角及其夹边分别相等的两个三角形全等.简记为“角边角”或“ASA”.判定两三角形全等的基本事实:角边角:1.判定方法二:两角及其夹边分别相等的两个三角形 全等(简记为“角边角”或“ASA”).2.证明书写格式:在△ABC和△A′B′C′中, ∵ ∴△ABC≌△A′B′C′.例1 已知:如图,点A,F,E,C在同一条直线上,AB∥DC,AB=CD,∠B=∠D.求证:△ABE≌△CDF.证明: ∵ AB∥DC,∴ ∠A=∠C.在△ABE和△CDF中,∴ △ABE≌△CDF (ASA).例2 如图, ∠1= ∠2,∠ 3= ∠4,求证:DB=CB.证明:∵ ∠DBA与∠3互为邻补角, ∠ABC与∠4互为邻补角,(已知) 又∵∠ 3= ∠4,∴ ∠ABD=∠ABC,(等角的补角相等)在△ABD和△ABC中,∠1= ∠2 ,(已知)AB=AB,(公共边)∠ABD=∠ABC,(已证) ∴ △ABD ≌ △ABC(ASA), ∴ DB=CB . 例3 如图,为测量河宽AB,小军从河岸的A点沿着和 AB垂直的方向走到C点,并在AC的中点E处立一根标杆,然后从C点沿着与AC垂直的方向走到D点,使D,E,B恰好在一条直线上. 于是小军说:“CD的长就是河的宽.”你能说出这个道理吗?BECD∠A =∠C = 90°,AE = CE,∠AEB =∠CED (对顶角相等),∴ △AEB≌△CED(ASA).∴ AB=CD (全等三角形的对应边相等).因此,CD的长就是河的宽度.1.已知:∠ABC=∠DCB,∠ACB= ∠DBC,求证:△ABC≌△DCB.∠ABC=∠DCB(已知), BC=CB(公共边), ∠ACB=∠DBC(已知),证明:在△ABC和△DCB中,∴△ABC≌△DCB(ASA ). 2.〈重庆〉如图,已知AB=AE,∠1=∠2, ∠B=∠E. 求证:BC=ED. 导引:要证BC=ED,需证它们所在的三角形全等, 由于∠B=∠E,AB=AE,因此需证∠BAC =∠EAD,即需证∠BAD+∠1=∠BAD+ ∠2.证明:∵∠1=∠2, ∴∠1+∠BAD=∠2+∠BAD, 即∠BAC=∠EAD. 在△BAC和△EAD中, ∴△BAC≌△EAD(ASA). ∴BC=ED.当堂练习1. 如图,在△ABC和△EBD中,AB=BE=8,∠A=∠E, 且BD=4,则CE的长是( ) A.4 B.5 C.6 D.72. 如图,AD、BC相交于点O,∠1=∠2,∠CAB= ∠DBA,下列结论中,错误的是( ) A.∠C=∠D B.AC=BD C.OC=OB D.BC=ADACABCDEF3.如图∠ACB=∠DFE,BC=EF,那么应补充一个条件 ,才能使△ABC≌△DEF (写出一个即可).∠B=∠E证明:在△ACD和△ABE中, ∠A=___( ), _______ ( ), ∠C=___( ),∴△ACD≌△ABE( ),∴AD=AE( ).分析:只要找出 ≌ ,得AD=AE. △ACD△ABE∠A公共角AB=AC∠BASA全等三角形的对应边相等 3.如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C. 求证:AD=AE.已知已知4. 已知:如图,△ABC≌△A′B′C′,CF,C′F′分别是∠ACB和∠A′C′B′的平分线. 求证:CF=C′F′.证明:∵△ABC≌△A′B′C′, ∠A =∠A′ , ∠ACB =∠A′C′B′.∴ AC=A′C′,∴ CF=C′F′. 又∵CF,C′F′分别是∠ACB和∠A′C′B′的平分线,∴ ∠ACF=∠A′C′F′.∴ △ACF≌△A′C′F′课堂小结两角及其夹边分别相等的两个三角形应用:证明角相等,边相等三角形全等的“ASA”判定:两角及其夹边分别相等的两个三角形全等.下 课
相关资料
更多










