





初中沪科版14.2 三角形全等的判定获奖课件ppt
展开1.掌握证明三角形全等的方法:AAS. (重点)2.理解不能判定两三角形全等三个对应元素:角角角和边边角.
证明三角形全等的方法还有哪些?
知识点1 判定两三角形全等的定理:角角边
我们知道,SAS,ASA,SSS都可以作为判定两个三角形全等的条件.其实,在三角形的六个基本元素中选择三个元素对应相等,除了可以配成SAS,ASA,SSS外,还可以配成:AAA,SSA,AAS .想一想,满足下面三组条件中任一组的两个三角形,即(1)三个角分别相等;(2)两边和其中一边的对角分别相等;(3)两角和其中一角的对边分别相等. 能判定这两个三角形全等吗?
1.判定方法四:两角分别相等且其中一组等角的对 边相等的两个三角形全等(简记为“角角边”或 “AAS”).2.证明书写格式:在△ABC和△A′B′C′中, ∵ ∴△ABC≌△A′B′C′.
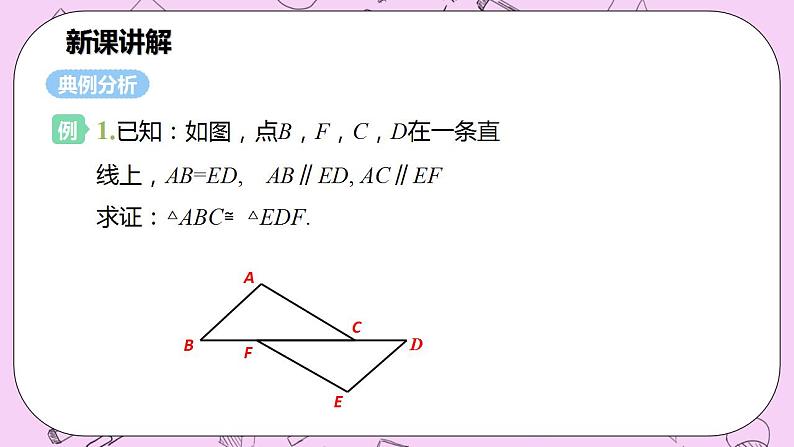
1.已知:如图,点B,F,C,D在一条直线上,AB=ED, AB∥ED, AC∥EF求证:△ABC≌△EDF.
证明 ∵ AB∥ED, AC∥EF∴∠B=∠D, ∠ACB=∠EFD 在△ABC与△EDF中 ∠B=∠D (已证) ∠ACB=∠EFD (已证) AB=ED (已知)∴△ABC≌△EDF(AAS)
知识点2 不能判定两三角形全等三个对应元素
如图,已知∠B=∠C,添加一个条件使△ABD≌△ACE(不标注新的字母,不添加新的线段),你添加的条件是___________________________________________________.
AB=AC或AD=AE或BD=CE或BE=CD(写出一个即可)
导引:本题给出∠B=∠C,再加上公共角∠A,有两个条件, 根据全等三角形的判定方法,有两个角相等的判定方 法有AAS,ASA,只要添加任意一组对应边相等即可, 即AB=AC或AD=AE或BD=CE;如果从已知给定的 条件中,通过添加另外一个条件能够得到AB=AC或 AD=AE或BD=CE中任意一个条件也可以,即BE= CD.
1.如图,下列条件中,不能证明△ABC≌△DCB的是( ) A.AB=DC,AC=DB B.AB=DC,∠ABC=∠DCB C.BO=CO,∠A=∠D D.AB=DC,∠DBC=∠ACB
2.以下四个命题中正确的是( ) A.有三个角对应相等的两个三角形全等 B.有两边对应相等的两个三角形全等 C.有一个角相等且有两条边相等的两个三角形全等 D.有一边相等的两个等边三角形全等3.已知下列条件不能作出唯一三角形的是( ) A.已知三边 B.已知两边及夹角 C.已知两角及夹边 D.已知两边以及其中一边的对角
4.如图:已知AD = AE ,∠B=∠C,△ABD与△ACE全等吗?为什么?
∴△ABD≌△ACE( AAS )
解:全等.在△ABD和△ACE∵
∠B=∠C(已知)∠A=∠A(公共角)AD=AE(已知)
初中数学沪科版八年级上册14.2 三角形全等的判定习题ppt课件: 这是一份初中数学沪科版八年级上册14.2 三角形全等的判定习题ppt课件,共26页。PPT课件主要包含了角角边,AAS,不一定,①②③等内容,欢迎下载使用。
数学八年级上册14.2 三角形全等的判定集体备课课件ppt: 这是一份数学八年级上册14.2 三角形全等的判定集体备课课件ppt,共8页。PPT课件主要包含了∴∠C∠P,ASA,∠B∠E,或∠A∠D,或ACDF,AAS,SAS,BECF已知,∠C∠E已知,AB∠AD已知等内容,欢迎下载使用。
初中数学沪科版八年级上册14.2 三角形全等的判定评课ppt课件: 这是一份初中数学沪科版八年级上册14.2 三角形全等的判定评课ppt课件,共20页。













