14.2.5《两个直角三角形全等的判定》课件

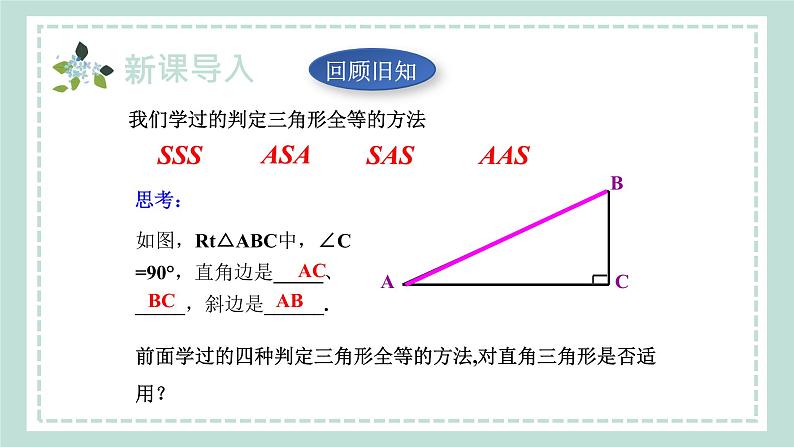
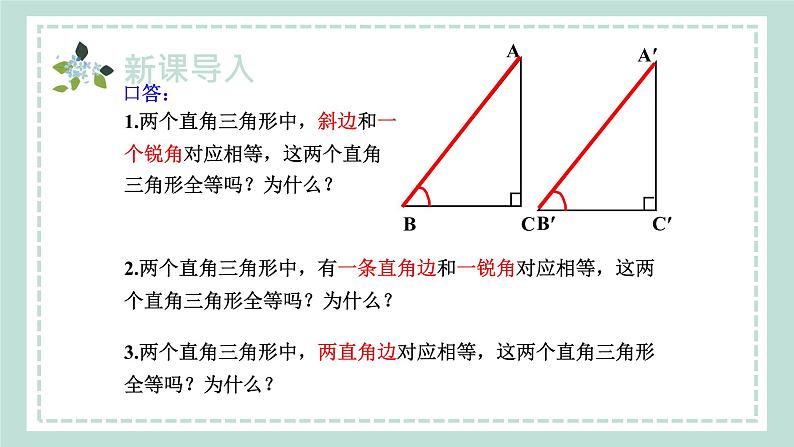
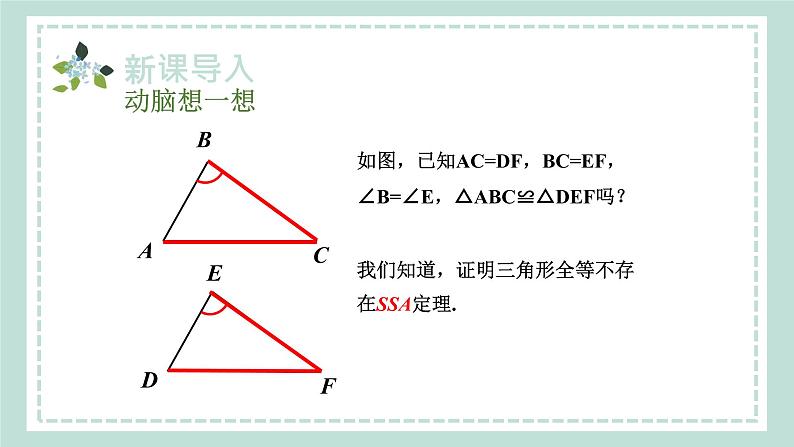
沪科版数学八年级上册14.2.5 两个直角三角形全等的判定新课导入讲授新课当堂练习课堂小结目录新课导入1．探索并理解直角三角形全等的判定方法“HL”．（难点）2．会用直角三角形全等的判定方法“HL”判定两个直角三角形全等．（重点）SSSSASASAAAS我们学过的判定三角形全等的方法如图，Rt△ABC中，∠C =90°，直角边是_____、_____，斜边是______.ACBCAB思考：前面学过的四种判定三角形全等的方法,对直角三角形是否适用？ABCA′B′C′1.两个直角三角形中，斜边和一个锐角对应相等，这两个直角三角形全等吗？为什么？2.两个直角三角形中，有一条直角边和一锐角对应相等，这两个直角三角形全等吗？为什么？3.两个直角三角形中，两直角边对应相等，这两个直角三角形全等吗？为什么？口答：动脑想一想如图，已知AC=DF，BC=EF，∠B=∠E，△ABC≌△DEF吗？我们知道，证明三角形全等不存在SSA定理.讲授新课直角三角形全等的判定 （“斜边、直角边”定理）问题：如果这两个三角形都是直角三角形，即∠B=∠E=90°，且AC=DF，BC=EF，现在能判定△ABC≌△DEF吗？ 任意画出一个Rt△ABC,使∠C=90°.再画一个Rt△A ′B ′C ′，使∠C′=90 °，B′C′=BC，A ′B ′=AB，把画好的Rt△A′B′ C′ 剪下来，放到Rt△ABC上，它们能重合吗？画图思路（1）先画∠M C′ N=90°（2）在射线C′M上截取B′C′=BCB′（3）以点B′为圆心，AB为半径画弧，交射线C′N于A′B′A′（4）连接A′B′B′A′思考：通过上面的探究，你能得出什么结论？“斜边、直角边”判定方法文字语言： 斜边和一条直角边对应相等的两个直角三角形全等（简写成“斜边、直角边”或“HL”）.几何语言： 在Rt△ABC和Rt△ A′B′C′ 中，∴Rt△ABC ≌ Rt△ A′B′C′ (HL).“SSA”可以判定两个直角三角形全等，但是“边边”指的是斜边和一直角边，而“角”指的是直角.判断满足下列条件的两个直角三角形是否全等，不全等的画“×”，全等的注明理由： （1）一个锐角和这个角的对边对应相等；（ ） （2）一个锐角和这个角的邻边对应相等；（ ） （3）一个锐角和斜边对应相等； （ ） （4）两直角边对应相等； （ ） （5）一条直角边和斜边对应相等． （ ）×HLSASAASAAS判一判 如图，∠BAC=∠CDB=90°， AC﹦DB，求证：AB﹦DC.证明： ∵∠BAC=∠CDB=90°， ∴△BAC,△CDB都是直角三角形.在 Rt△BCD 和Rt△CBA中，∴ Rt△BCD≌Rt△CBA (HL).∴ AB=DC. 变式1： 如图， ∠ACB =∠ADB=90，要证明△ABC≌ △BAD，还需一个什么条件？把这些条件都写出来，并在相应的括号内填写出判定它们全等的理由. （1） （ ） （2） （ ） （3） （ ） （4） （ ）AD=BC∠ DAB= ∠ CBABD=AC∠ DBA= ∠ CABHL HLAASAAS如图，AC、BD相交于点P,AC⊥BC，BD⊥AD，垂足分别为C、D,AD=BC.求证：AC=BD.变式2HLAC=BDRt△ABD≌Rt△BAC如图：AB⊥AD，CD⊥BC，AB=CD,判断AD和BC的位置关系.变式3HL∠ADB=∠CBDRt△ABD≌Rt△CDBAD∥BC 如图，已知AD，AF分别是两个钝角△ABC和△ABE的高，如果AD＝AF，AC＝AE. 求证：BC＝BE.证明：∵AD，AF分别是两个钝角△ABC和△ABE的高，且AD＝AF，AC＝AE，∴Rt△ADC≌Rt△AFE(HL)．∴CD＝EF.∵AD＝AF，AB＝AB，∴Rt△ABD≌Rt△ABF(HL)．∴BD＝BF.∴BD－CD＝BF－EF.即BC＝BE. 证明线段相等可通过证明三角形全等解决，作为“HL”公理就是直角三角形独有的判定方法．所以直角三角形的判定方法最多，使用时应该抓住“直角”这个隐含的已知条件． 如图，有两个长度相同的滑梯，左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，两个滑梯的倾斜角∠B和∠F的大小有什么关系？解：在Rt△ABC和Rt△DEF中,∴ Rt△ABC≌Rt△DEF (HL).∴∠B=∠DEF(全等三角形对应角相等).∵ ∠DEF+∠F=90°,∴∠B+∠F=90°.当堂练习1．下列条件不能使两个直角三角形全等的是(　　) A．斜边和一锐角对应相等 B．有两边对应相等 C．有两个锐角对应相等 D．有一直角边和一锐角对应相等2．如图，在△ABC中，∠C＝90°，ED⊥AB于点D， BD＝BC，若AC＝6 cm，则AE＋DE等于(　　) A．4 cm B．5 cm C．6 cm D．7 cm C C3．如图，∠ACB＝90°，AC＝BC，BE⊥CE于点E， AD⊥CE于点D，下面四个结论：① ∠ABE＝∠BAD；②△CEB≌△ADC； ③AB＝CE；④AD－BE＝DE.其中正确 的是________．4．如图，MN∥PQ，AB⊥PQ，点A，D在直线MN上，点B，C在直线PQ上，点E在AB上， AD＋BC＝7，AD＝EB，DE＝EC， 则AB＝________. ①②④ 75．如图，在△ABC中，AB＝CB，∠ABC＝90°，F为AB延长线上一点，点E在BC上，且AE＝CF.求证： Rt△ABE≌Rt△CBF.证明： ∵∠ABC＝90°， ∴∠CBF＝∠ABE＝90°. 在Rt△ABE和Rt△CBF中， ∵AE＝CF，AB＝CB， ∴Rt△ABE≌Rt△CBF(HL)．6．如图，AB=CD, BF⊥AC,DE⊥AC,AE=CF. 求证：BF=DE.证明: ∵ BF⊥AC,DE⊥AC, ∴∠BFA=∠DEC=90 °.∵AE=CF， ∴AE+EF=CF+EF.即AF=CE.在Rt△ABF和Rt△CDE中，∴ Rt△ABF≌Rt△CDE(HL).∴BF=DE.如图，AB=CD, BF⊥AC,DE⊥AC,AE=CF.求证：BD平分EF.变式训练1Rt△ABF≌Rt△CDE(HL).BF=DERt△GBF≌Rt△GDE(AAS).∠BFG=∠DEG∠BGF=∠DGEFG=EGBD平分EF如图，AB=CD, BF⊥AC,DE⊥AC,AE=CF.想想：BD平分EF吗?变式训练2Rt△ABF≌Rt△CDE(HL).BF=DERt△GBF≌Rt△GDE(AAS).∠BFG=∠DEG∠BGF=∠DGEFG=EGBD平分EF7.如图，有一直角三角形ABC，∠C＝90°，AC＝10cm，BC＝5cm，一条线段PQ＝AB，P、Q两点分别在AC上和过A点且垂直于AC的射线AQ上运动，问P点运动到AC上什么位置时△ABC才能和△APQ全等？分析：本题要分情况讨论：(1)Rt△APQ≌Rt△CBA，此时AP＝BC＝5cm，可据此求出P点的位置．(2)Rt△QAP≌Rt△BCA，此时AP＝AC，P、C重合．能力拓展解：(1)当P运动到AP＝BC时， ∵∠C＝∠QAP＝90°. 在Rt△ABC与Rt△QPA中， ∵PQ＝AB，AP＝BC， ∴Rt△ABC≌Rt△QPA(HL)， ∴AP＝BC＝5cm；(2)当P运动到与C点重合时，AP＝AC. 在Rt△ABC与Rt△QPA中，∵PQ＝AB，AP＝AC，∴Rt△QAP≌Rt△BCA(HL)，∴AP＝AC＝10cm，∴当AP＝5cm或10cm时，△ABC才能和△APQ全等．方法总结：判定三角形全等的关键是找对应边和对应角，由于本题没有说明全等三角形的对应边和对应角，因此要分类讨论，以免漏解．课堂小结“斜边、直角边”内容斜边和一条直角边对应相等的两个直角三角形全等.前提条件在直角三角形中使用方法只须找除直角外的两个条件即可（两个条件中至少有一个条件是一对对应边相等）下 课