初中数学16.1 二次根式精品巩固练习

16.1 二次根式

一、二次根式的概念

1、概念：形如 (≥0)的式子叫做二次根式，“”称为二次根号。

注：①二次根式表示代数式的算术平方根；

②被开放数可以表示数字、字母、或代数式。

2、二次根式的识别方法

判断一个式子是否为二次根式，看所给的式子是否同时具备二次根式的两个特征：

（1）含有二次根号“”；（2）被开方数必须是非负数。

3、判断二次根式有无意义的条件

（1）被开方数是非负数；

（2）如果一个式子中含有多个二次根式，那么它们有意义的条件是：各个二次根式中的被开方数都是非负数；

（3）如果所给式子中含有分母，则除了保证被开方数为非负数外，还要保证分母不为零。

二、二次根式的性质

性质1. (双重非负性)

性质2.

性质3.

注：与的区别

三、代数式

概念：用基本运算符号(基本运算包括加、减、乘、除、乘方和开方)把数或表示数的字母连接起来的式子，我们称这样的式子为代数式。

注：代数式中不含有关系符号(“=”“>”或“<”等)。

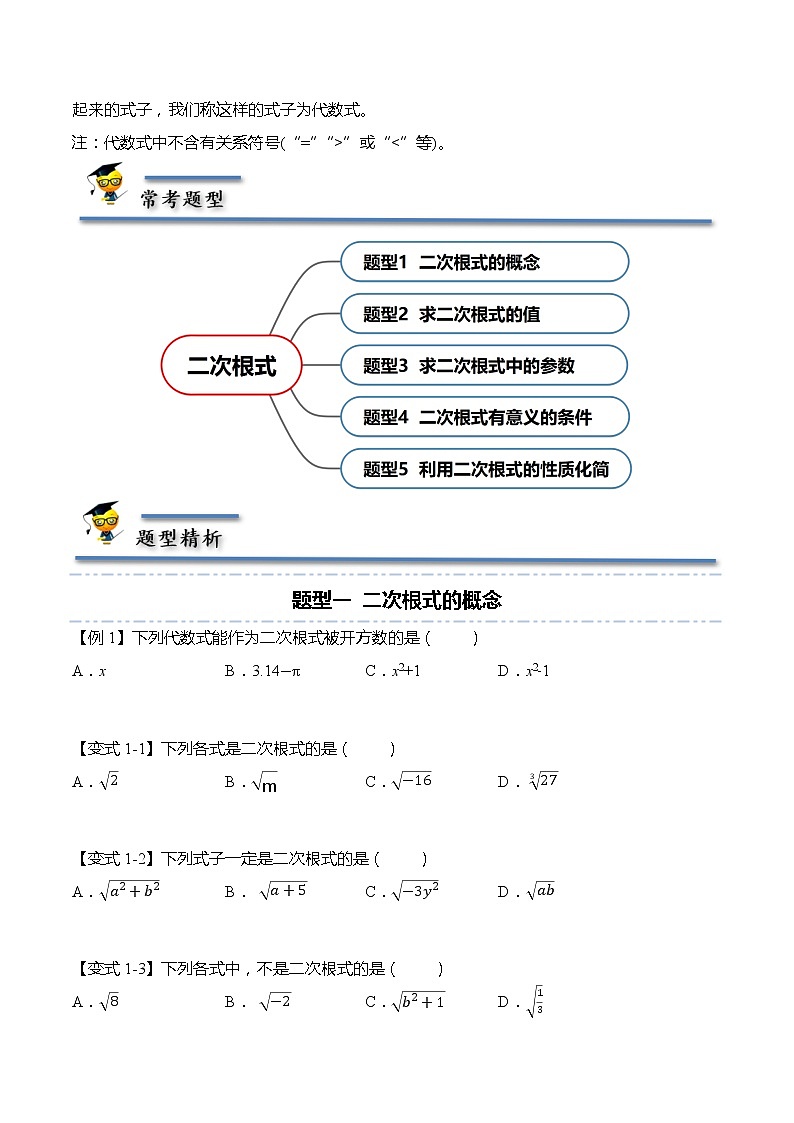
题型一 二次根式的概念

【例1】下列代数式能作为二次根式被开方数的是（　　）

A．x B．3.14π C．x2+1 D．x2﹣1

【答案】C

【解析】∵x2+1＞0，∴x2+1能作为二次根式被开方数．故选C．

【变式1-1】下列各式是二次根式的是（　　）

A． B． C． D．

【答案】A

【解析】A、2＞0一定成立，被开方数是非负数；B、当m＜0时，二次根式无意义；

C、被开方数为负数，二次根式无意义；D、是三次根式． 故选A．

【变式1-2】下列式子一定是二次根式的是（　　）

A． B．  C． D．

【答案】A

【解析】A、中被开方数是非负数，是二次根式；

B、中，当a＜5时，被开方数是负数，不是二次根式；

C、中，y≠0时，被开方数是负数，不是二次根式；

D、中，当ab＜0时，被开方数是负数，不是二次根式．故选A．

【变式1-3】下列各式中，不是二次根式的是（　　）

A． B．  C． D．

【答案】B

【变式1-4】下列式子是二次根式的有（　　）个

A．2 B．3 C．4 D．5

【答案】B

【解析】，

所以和，是二次根式．故选B．

题型二 求二次根式的值

【例2】计算下列各式

（1） （2） （3）（4）

【答案】（1）（2）  （3）（4）

【解析】（1）

（2）

（3）

（4）

【变式2-1】二次根式的值等于（　　）

A．﹣2 B．±2 C．2 D．4

【答案】C

【解析】原式＝|﹣2|＝2．故选C．

【变式2-2】当x＝1时，二次根式的值等于（　　）

A．4 B．0 C． D．2

【答案】C

【解析】当x＝1时，二次根式故选C．

【变式2-3】已知x，y都是实数，且，则y＝　  　．

【答案】4

【解析】∵，∴，解得x＝3，∴y＝4.

题型三 求二次根式中的参数

【例3】已知二次根式的值为4，那么x的值是（　　）

A．4 B．16 C．4 D．4或4

【答案】D

【解析】依题意得，＝4．则x2＝16，解得x＝±4．故选D．

【变式3-1】若是整数，则正整数n的最小值是（　　）

A．3 B．7 C．9 D．63

【答案】B

【解析】∵，且是整数；

∴3是整数，即7n是完全平方数；

∴n的最小正整数值为7．故选B．

【变式3-2】为任意实数，满足，则的值是（　　）

A．2020 B．2021 C．2022 D．无法确定

【答案】C

【解析】根据题意，得：，即，

∴由，

得：，即，

两边平方，得

∴．故选C．

【变式3-3】 成立的条件是（　　）

A． B． C． D．-

【答案】C

【解析】根据题意，得：，∴，故选C．

【变式3-4】已知，则的平方根为（　　）

A． B． C．2 D．2

【答案】B

【解析】由题意得：，解得：x＝，

∴y＝1，∴，

∴2的平方根是．故选B．

题型四 二次根式有意义的条件

【例4】求使下列各式有意义的字母的取值范围：

（1）（2）（3）（4）（5）（6）（7）

【答案】（1）x≥﹣5；（2）a≤3；（3）a≥；（4）x≥0；（5）k＞﹣1；（6）x≥﹣2且x≠2；

（7）x≥5

【解析】（1）x+5≥0，∴x≥﹣5；

（2）3﹣a≥0，﹣a≥﹣3，∴a≤3；

（3）2a+1≥0，2a≥﹣1，∴a≥；

（4）8x≥0，∴x≥0．

（5）k+1＞0，∴k＞﹣1．

（6），解得x≥﹣2且x≠2．

（7）x﹣5≥0，∴x≥5

【变式4-1】若x为整数，且满足，则当也为整数时，则x的值可以是 　          　．

【答案】﹣3或﹣2或﹣1或0或1或2或﹣2

【解析】∵|x|＜π且2﹣x≥0，

∴﹣π＜x≤2，

∵也为整数，

∴x的值可以是：﹣3或﹣2或﹣1或0或1或2或﹣2．

【变式4-2】代数式有意义，则x的取值范围在数轴上表示正确的是（　　）

A． B． 

C． D．

【答案】D

【解析】根据题意知，1﹣x＞0，解得x＜1，故选D．

【变式4-3】若式子有意义，则点P（a，b）在（　　）

A．第一象限 B．第二象限 C．第三象限 D．第四象限

【答案】B

【解析】由题意得，﹣a＞0，b＞0，∴a＜0，∴点P（a，b）在第二象限．故选B．

【变式4-4】使函数有意义的所有整数的和是（　　）

A．2 B．1 C．0 D．1

【答案】A

【解析】由题意可知：，，解得，

∴使得原式有意义的所有整数有，

∴使得原式有意义的所有整数和为．故选A．

【变式4-5】若二次根式有意义，且关于x的方程有正整数解，则符合条件的整数m的积是（　　）

A．3 B．3 C．1 D．1

【答案】C

【解析】整理方程，可得： ，

解方程，可得：x＝，

由题意可得，且m为整数，为正整数，

解得符合条件的整数m的值为1、1，

∴1×1＝1，故选C．

题型五 利用二次根式的性质化简

【例5】x、y均为实数，化简：．

【答案】解：由题意得，且，

解得x≥1且x≤1，

∴x＝1，y＜，

∴．

【变式5-1】若x、y为实数，，化简：．

【答案】解：∵和有意义，

∴，解得x＝2，∴y＜1，

∴

【变式5-2】若实数x、y满足y＜．

（1）x＝　 　，y＜　 　；

（2）化简：．

【答案】（1）1,1 （2）见解析

【解析】（1）由题意可知：，∴x＝1，∴y＜1故答案为：1，1；

（2）解：∵y＜1，

∴＜0，＞0，

原式＝

【变式5-3】（1）计算；

（2）已知，求的立方根．

【答案】解：（1）原式＝

（2）由题意可得， 解得：x＝2，

∴，

∴原式＝

＝，

的立方根为，

∴的立方根为．

【变式5-4】（1）若，求的值；

（2）若a，b互为相反数，c，d互为倒数，m的绝对值为2，求的值.

【答案】解：（1）由题意，得

解得x＝8．

∴y＝16

∴原式＝＝2﹣4＝﹣2．

（2）∵a，b互为相反数，c，d互为倒数，m的绝对值为2，

∴a+b＝0，cd＝1，m＝±2，

∴．

当m＝2时，原式＝1．

当m＝2时，原式＝．