初中第九章 不等式与不等式组9.2 一元一次不等式教学演示ppt课件

这是一份初中第九章 不等式与不等式组9.2 一元一次不等式教学演示ppt课件，共20页。PPT课件主要包含了一元一次不等式，③－2x＜5，①3＋5＞7，②x－y≤2，⑦2x－3＞1，⑥3m－2＜n＋7，⑤x2＋3＜2，⑧3－2a≥5，x-5等内容，欢迎下载使用。
1.什么叫一元一次方程 ?
只含有一个未知数、并且未知数的次数都是“1”，等号两边都是整式，这样的方程叫做一元一次方程.
2.不等式的基本性质：
不等式性质1:不等式两边加(或减)同一个数（或式子），不等号的方向不变.不等式性质2:不等式两边都乘（或除以）同一个正数，不等号的方向不变.
不等式性质3：不等式两边都乘（或除以）同一个负数，不等号的方向改变.
有一次，鲁班的手不慎被一片小草叶子割破了，他发现小草叶子的边缘布满了密集的小齿，于是便产生联想，根据小草的结构发明了锯子.
鲁班在这里就运用了“类比”的思想方法，“类比”也是数学学习中常用的一种重要方法.
含有一个未知数，未知数的次数是1的不等式，叫做一元一次不等式.
你能给这类不等式起个名字吗？
相同点：都只含有一个未知数，且未知数的次数都是1
不同点：一元一次方程表示的是相等关系 而以上式子则表示的是不等关系.
练一练：下列不等式中，哪些是一元一次不等式？
一元一次不等式判别条件：(1)都是整式；(2)只含一个未知数；(3)未知数的最高次数是1；(4)未知数的系数不为0.
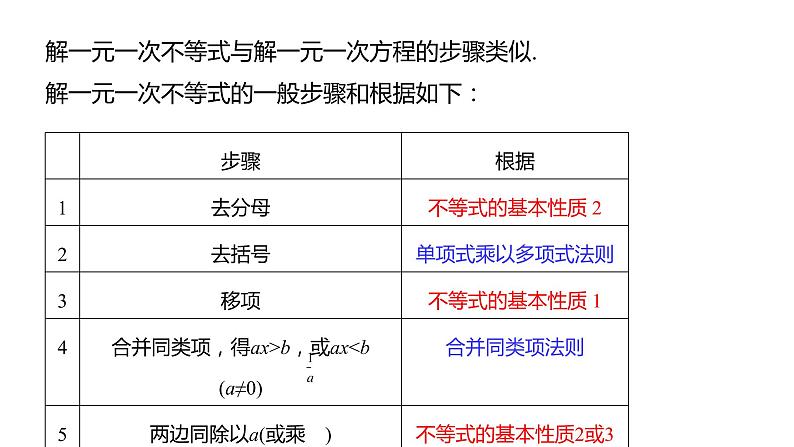
解一元一次不等式与解一元一次方程的步骤类似. 解一元一次不等式的一般步骤和根据如下：
(2) 去分母，得 3(2+x)≥2(2x-1). 去括号，得 6+3x ≥4 x-2 . 移项，得 3x- 4x ≤ -2-6 . 合并同类项，得 -x ≥ -8 . 系数化为1，得 x ≤ 8 . 这个不等式的解集在数轴上的表示如图所示 .
注意：当不等式的两边都乘（或除以）同一个负数时，不等号的方向改变！
解一元一次方程,要根据等式的性质,将方程逐步化为 x =a 的形式;而解一元一次不等式,则要根据不等式的性质,将不等式逐步化为 xa 的形式.
例2 求不等式3(x＋1)≥5x－9的非负整数解．
分析：求不等式的非负整数解，即在原不等式的解集中找出它所包含的“非负整数”特殊解；因此先需求出原不等式的解集．
解：∵解不等式3(x＋1)≥5x－9得x≤6.在数轴上表示为：∴不等式3(x＋1)≥5x－9的非负整数解为 0，1，2，3，4，5，6.
注意：在确定特殊解时，一定要注意是否包括端点的值，一般可以结合数轴，形象直观，一目了然．
例3 当x取何值时，代数式 与 的值的差大于1？
去分母，得 2(x+4)-3(3x-1)>6.去括号，得 2x+8-9x+3>6，合并同类项，得 -7x+11>6.移项，得 -7x >-5.
1．下列不等式中，是一元一次不等式的是(　　)A．2x－1＞0 B．－1＜2 C．3x－2y≤－1 D．y2＋3＞5
3．不等式4－3x≥2x－6的非负整数解有(　　)A．1个 B．2个 C．3个 D．4个
5. 解下列不等式，并在数轴上表示解集：(1) 5x＋15＞4x－1；
解：(1)移项，得5x－4x>－1－15， 合并同类项，得x>－16. 这个不等式的解集在数轴上的表示．
解：去括号，得2x＋10≤3x－15， 移项，得2x－3x≤－15－10， 合并同类项，得－x≤－25， 系数化为1，得x≥25. 这个不等式的解集在数轴上的表示．
(2) 2(x＋5)≤3(x－5)；