





- 四 长方体(二) 长方体的体积(2) 第5课时 课件+教案 课件 18 次下载
- 四 长方体(二) 有趣的测量 第7课时 课件+教案 课件 16 次下载
- 五 分数除法 分数除法(一) 第1课时 课件+教案 课件 19 次下载
- 五 分数除法 分数除法(二) 第2课时 课件+教案 课件 21 次下载
- 五 分数除法 分数除法(三) 第3课时 课件+教案 课件 18 次下载
四 长方体(二) 练习四 课件+教案
展开北师五下第四单元长方体(二) 练习四 | |||
课题 | 练习四 | 课型 | 新授课 |
教材分析 | 本节课是在学习了第四单元的以后的整理与复习的内容。一共13道习题。侧重在解决问题的过程中,进一步理解体积的含义,感受体积、容积单位的实际意义,运用长方体、正方体体积公式进行计算。 | ||
学情分析 | 学生首先回顾本单元内容,然后利用所学知识解决问题。鼓励学生咋不同的情境中,综合自己对题意、所学知识的理解来解决问题,提高学生分析问题、解决问题的能力。 | ||
教学策略 |
| ||
教学内容 | 北师大版五年级下册 教科书第 页 | ||
教学目标 |
| ||
教学重点 | 教学重点:回顾梳理体积、容积等知识,沟通知识间的联系,培养自我反思和整理所学知识的意识。 | ||
教学难点 | 教学难点:复习并掌握长方体等立体图形体积的计算方法,不规则物体体积的测量方法,进一步理解所学内容,发展空间观念。 | ||
教学准备 | 多媒体课件 | ||
课时安排 | 1课时 | ||
教学环节 | 导学案 | ||
一、创设情境
|
今天我们来学习第四单元第7课时《练习四》。
一、谈话导入 师:同学们,回想一下第四单元长方体学了哪些内容吧!
| ||
二、探究体验
经历过程 | 二、回顾梳理
| ||
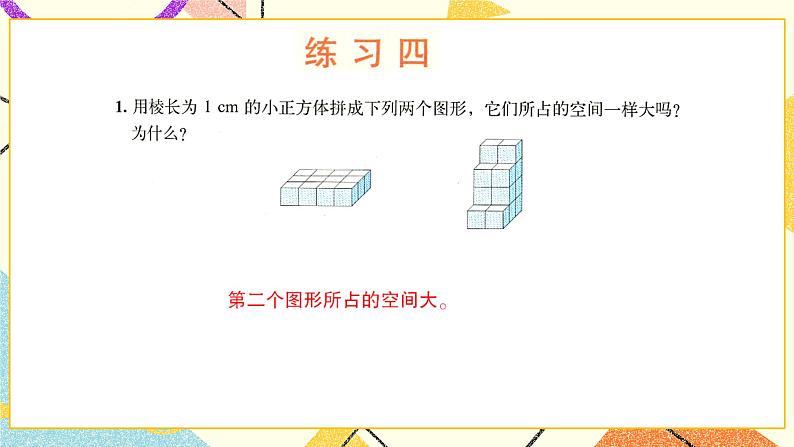
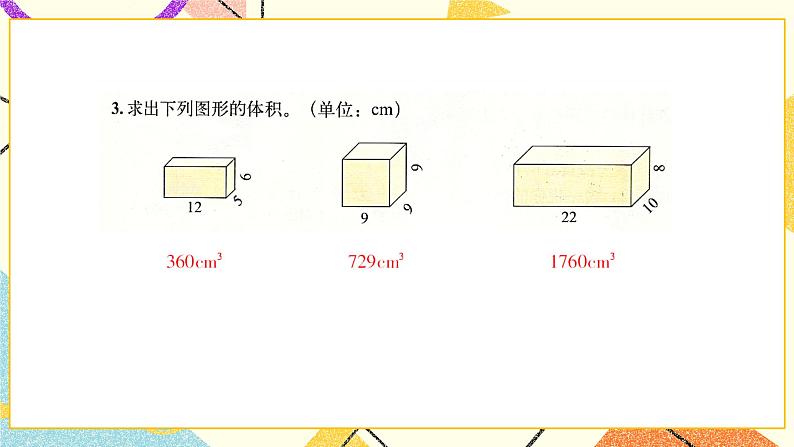
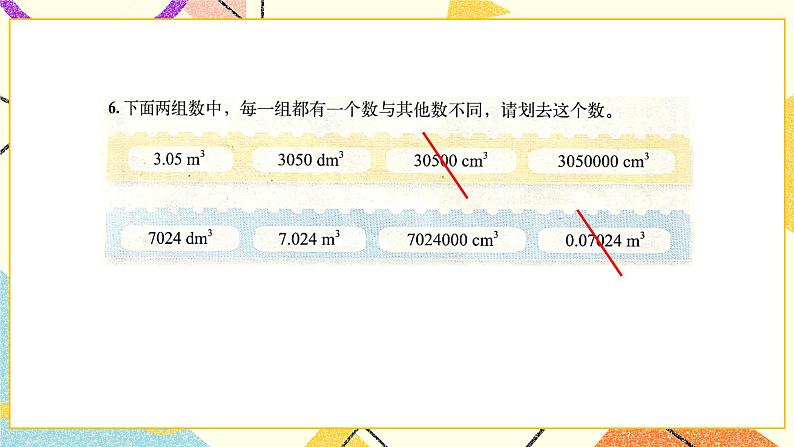
三、达标检测 | 三、习题精讲 师:1.用棱长为1cm的小正方体拼成下列两个图形,它们所占的空间一样大吗?为什么? 师:分析:包含多少个棱长为1cm小正方体,体积就是多少立方厘米 师:第一个图形的体积为12cm3 第二个图形的体积为16cm3 答:第二个图形所占的空间大。 师:2.填上适当的单位。 一块橡皮的体积约是10 立方厘米 一个文具盒的体积约是0.35 立方分米 一个词典的体积约是900 立方厘米 一个讲台的体积约是0.6 立方米 师:3.求出下列图形的体积。 第一个图形, 长乘宽乘高 12×5×6 =60×6 =360(dm3) 第二个图形是正方体 棱长乘棱长乘棱长 9×9×9 =729(cm3) 第三个图形 长乘宽乘高 22×10×8 =220×8 =1760(cm3) 师:4.一个长方体的长是12cm,宽是长的1/3 ,高是长的1/4 ,这个长方体的体积是多少? 师:先求出这个长方体的宽和高。 求一个数的几分之几是多少用乘法计算。 12×1/3=4(cm) 12×1/4=3(cm) 公式:长方体的体积=长乘宽乘高 12×4×3 =48×3 =144(cm3) 答:这个长方体的体积是144立方厘米。 师:5.换算单位,先回想一下体积和容积单位之间的进率吧。 1m3=1000dm3 1dm3=1000cm3 1L=1000mL 0.35m3=(350 )dm3 2.04dm3=( 2040 )cm3 5300dm3=(5.3 )m3 2800cm3=( 2.8 )dm3 19.6L=(19600 )mL 1325mL=(1.325 )L 师:6.下面两组数中,每一组都有一个数与其他数不同,请划去这个数。 我们发现每组数中的数单位不统一,先换算成统一的单位再进行观察。 3.05m3 3050dm3 30500cm3 3050000cm3 可以先把第一组数都换算成以平方厘米为单位的数。 1m3=1000000cm3 3.05m3 =3050000cm3 1dm3=1000cm3 3050dm3=3050000cm3 通过观察发现,第三个数30500cm3和其他数不一样,划去。 7024dm3 7.024m3 7024000cm3 0.07024m3 可以先把第二组数都换算成以平方分米为单位的数。 第二个数 7.024m3 =7024dm3 第三个数 7024000cm3 =7024dm3 第四个数 0.07024m3=70.24dm3 通过观察发现,第四个数 0.07024m3和其他数不一样,划去。 师:7.一个棱长为6cm的正方体药盒,它的表面积和体积分别是多少? 师:我们知道正方体的6个面大小都相同。 师:先求表面积。 6乘6是正方体一个面的面积,再乘6就是个面的表面积。 6×6×6 =36×6 =216(cm2) 再求体积。 正方体的体积=棱长乘棱长乘棱长 6×6×6 =36×6 =216(cm3) 答:正方体的表面积是216平方厘米,体积是216立方厘米。 师:注意哦! 面积单位是平方厘米,体积的单位是立方厘米哦! 师:8.一个长方体水箱的容积是200L,这个水箱的底面是一个边长为50cm的正方形,水箱的高是多少厘米? 师:(小视频)首先发现题目中给的数据单位不统一,先进行单位换算。 200L=200dm3 50cm=5dm 5×5=25(dm2) 8dm=80cm 答:水箱的高是80厘米。 师:9.在一块如右图的长方形地面上铺一层6cm厚的沙土。(单位:m) (1)需要多少立方米的沙土? 分析:沙土的厚度也就是长方体沙土的高 45×28×6 =1260×6 =7560(cm3) 7560cm3=75.6m3 答:需要75.6立方米的沙土。 师:(2)一辆车每次运送1.5m3的沙土,至少需要运多少次? 75.6 ÷1.5=50.4(次) 50+1=51(次) 答:至少需要运51次。 师:10.如图,一种旅行包的A、B、C三部分用拉链连接,拆卸方便。这种旅行包可以近似地看成是由右边的三个图形组成的,这个旅行包的容积大约是多少?(单位:cm) 师:第一种方法,我可以分别算三个长方体的体积再相加,就是这个旅行包的体积。 7×15×26 =105×26 =2730(cm3) 40×15×26 =600×26 =15600(cm3) 2730×2+15600 =5460+15600 =21060(cm3) 师:第二种方法,把这个旅行包看成一个大的个长方体进行计算。 7+40+7=54(cm3) 54×15×26 =810×26 =21060cm3) 答:这个旅行包的容积大约是21060cm3。 师:11.做一个如右图的无盖长方体铁皮水槽最少需要多大面积的铁皮?这个水槽最多可以盛多少升水?(单位:dm) 师:表面积: 12×5=60(cm2) 12×2×2=48(cm2) 5×2×2=20(cm2) 60+48+20=128(cm2) 体积: 12×5×2 =60×2 =120(cm3) =120(L) 答:水槽最少需要128立方厘米的铁皮,最多可以盛120升水。 师:12.某汽车油箱的长、宽、高如右图所示。(单位:cm) (1)这个油箱能装多少升汽油? 50×40×30 =2000×30 =60000(cm3) =60(dm3) 60dm3=60L 答:这个油箱能装60升汽油。 师:(2)如果每升汽油可行驶10km,这箱油最多可以供这辆汽车行驶多少千米? 用乘法计算。 10×60=600(千米) 答:这箱油最多可以供这辆汽车行驶600千米。 师:13.实践活动。找一些棱长为1cm的小正方体,做下面的活动。 师:(1)用4个这样的小正方体可以摆成一个大正方体吗? 一起来看图示,4个这样的小正方体不可以摆成一个大正方体。 师:(2)最少要用多少个这样的小正方体才可以摆成一个再大一点的正方体? 一起来看图示,至少要8个这样的小正方体不可以摆成一个再大一点正方体。 师:(3)你能再摆一个更大一点的正方体吗?用了多少个小正方体? 一起来看图示,至少要27个这样的小正方体不可以摆成一个更大一点正方体。
| ||
四、课堂小结 | 四、课堂小结 师:通过这节课的学习活动,你有什么收获? 师: 体积和容积 体积单位(一) 体积单位(二) 长方体的体积 体积单位的换算 有趣的测量 | ||
五、教学板书 |
练习四
| ||
六、教学反思 |
优点:这节课非常注重学生创新能力的培养,发挥生活中常见的现象给人的冲击作用,物体沉入水中水面会上升,让学生理解排水法的原理所在。空间观念在此时进一步深化,以另一种非常规的形态被学生所接受。 缺点:学生在测量时,要注意物体要完全沉浸在水中,观察刻度时要保持水平状态。 改进措施:学生在实际操作和测量中,由于操作不规范会存在误差,提醒同学要规范测量。
| ||










