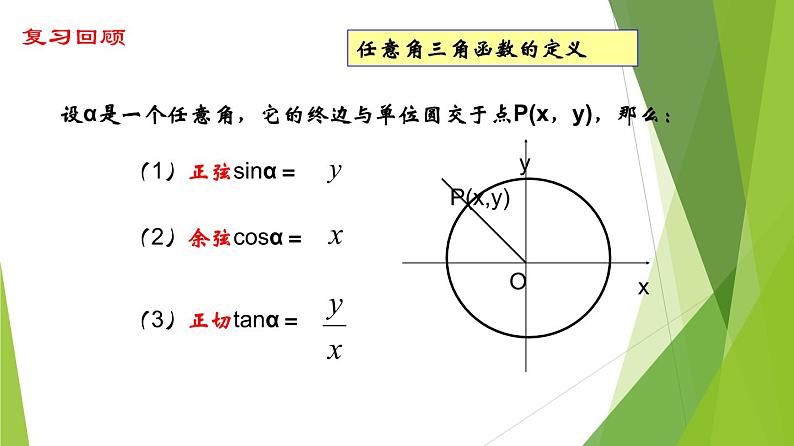
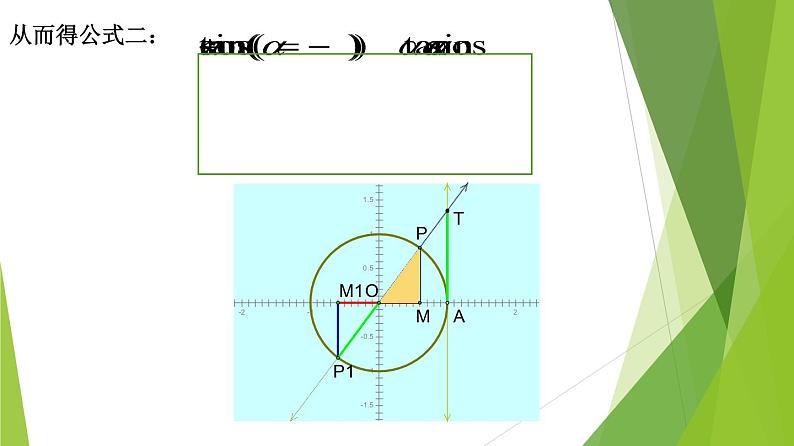
人教A版 (2019)必修 第一册5.3 诱导公式备课课件ppt

5.3 诱导公式（分层作业）（夯实基础+能力提升）

【夯实基础】

一、单选题

1．（2022·全国·高一课时练习）化简（    ）

A． B． C． D．

2．（2022·全国·高一课时练习）的值是（    ）

A． B． C． D．

3．（2022·全国·高一课时练习）若，则（    ）

A． B． C． D．

4．（2022·重庆复旦中学高一开学考试）化简的值是（    ）

A． B． C． D．

5．（2022·西藏拉萨·高一期末）（    ）

A． B． C． D．1

二、多选题

6．（2022·安徽省宿州市苐三中学高一期中）下列结论中，正确的有（    ）

A． B．

C． D．

7．（2022·全国·高一课时练习）已知角满足，则的取值可能为（    ）

A． B． C． D．

8．（2022·山东东营·高一期中）在平面直角坐标系中，角的始边为 的正半轴，终边经过点，则下列式子正确的是（    ）

A． B．

C． D．若为钝角，则

三、填空题

9．（2022·全国·高一课时练习）计算：______.

10．（2022·全国·高一学业考试）已知，则______．

11．（2022·全国·高一课时练习）已知角的顶点在坐标原点，始边与x轴非负半轴重合，终边经过点，则的值为______．

12．（2022·湖北·郧阳中学高一阶段练习）若，则__________．

13．（2022·江苏·南京市第一中学高一阶段练习）若，则______．

14．（2022·浙江省杭州学军中学高一期中）已知钝角终边上一点的坐标为，则________.

15．（2022·浙江大学附属中学高一期中）计算：________．

四、解答题

16．（2022·西藏拉萨·高一期末）已知为第三象限角，且．

(1)化简；

(2)若，求的值．

17．（2022·山东东营·高一期中）已知角满足

(1)若角是第三象限角，求的值;

(2)若，求的值.

18．（2022·湖北宜昌·高一阶段练习）已知．

(1)求的值；

(2)若为第四象限角，求的值．

19．（2022·陕西·蒲城县蒲城中学高一期末）（1）计算：；

（2）已知，求的值.

20．（2022·浙江·杭州高级中学高一期末）（1）化简；

（2）已知关于的方程的两根为和，.求实数以及的值.

【能力提升】

一、单选题

1．（2022·全国·高一课时练习）已知，则（    ）

A． B． C． D．

2．（2022·内蒙古大学满洲里学院附属中学高一期末）已知f（x）是定义在R上的偶函数，在[0，+∞）上是增函数，若a=f（sin），b=f（cos），c=f（tan），则（　　）

A．a＞b＞c B．c＞a＞b C．b＞a＞c D．c＞b＞a

二、多选题

3．（2022·全国·高一课时练习）在平面直角坐标系中，点，，，则下列说法正确的是（    ）

A．线段与的长均为1 B．线段的长为1

C．当时，点，关于轴对称 D．当时，点，关于轴对称

4．（2022·全国·高一课时练习）已知函数，则（    ）

A． B．

C．， D．，

5．（2022·全国·高一课时练习）定义：角与都是任意角，若满足，则称与“广义互余”.已知，则下列角中，可能与角“广义互余”的是（    ）

A． B． C． D．

6．（2022·全国·高一课时练习）在平面直角坐标系xOy中，点，，，则下列说法正确的是（    ）

A．线段与的长均为1 B．线段的长为1

C．当时，点，关于y轴对称 D．当时，点，关于x轴对称

三、填空题

7．（2022·北京·牛栏山一中高一阶段练习）已知角的终边经过点，将角的终边绕原点顺时针旋转得到角的终边，则___________.

8．（2022·全国·高一专题练习）______．

四、解答题

9．（2022·安徽省舒城中学高一开学考试）已知α是第三象限角，且.

(1)化简；

(2)若，求；

(3)若，求.

10．（2022·全国·高一课时练习）已知，为第二象限角.

(1)若，求的值；

(2)若，求的值.

11．（2022·全国·高一课时练习）已知角的终边过点．

(1)求的值；

(2)求的值．

12．（2022·全国·高一课时练习）已知函数.

(1)化简；

(2)若，求的值.

13．（2022·江西上饶·高一阶段练习）在平面直角坐标系中，的顶点与坐标原点重合，点在轴的正半轴上，点在第二象限，且，记，满足．

(1)求点的坐标；

(2)求的值．

14．（2022·陕西·宝鸡市渭滨区教研室高一期末）已知 .

(1)化简；

(2)若是第四象限角，且 ，求的值.

15．（2022·辽宁沈阳·高一期中）已知，且函数．

(1)化简；

(2)若，求和的值．

16．（2022·全国·高一）（1）已知，求的值．

（2）化简．

17．（2022·北京育才学校高一阶段练习）已知，

(1)求的值；

(2)求的值．

18．（2022·全国·高一课时练习）已知正弦三倍角公式：①

（1）试用公式①推导余弦三倍角公式（仅用表示）；

（2）若角满足，求的值.

19．（2022·江西抚州·高一期末）已知O为坐标原点，对于函数，称向量为函数的相伴特征向量，同时称函数为向量的相伴函数.

（1）设函数，试求的相伴特征向量；

（2）记向量的相伴函数为，求当且，的值；

（3）已知，，为的相伴特征向量，，请问在的图象上是否存在一点P，使得.若存在，求出P点坐标；若不存在，说明理由.

20．（2022·全国·高一课时练习）如果函数的定义域为，对于定义域内的任意存在实数使得成立，则称此函数具有“性质”.

（1）判断函数是否具有“性质”，若具有“性质”，写出所有的值；若不具有“性质”，请说明理由.

（2）设函数具有“性质”，且当时，，求当时函数的解析式；若与交点个数为1001个，求的值.