初中数学北师大版九年级下册1 二次函数优质课ppt课件

这是一份初中数学北师大版九年级下册1 二次函数优质课ppt课件，共18页。PPT课件主要包含了学习目标，温故知新，知识讲解，y2x2+1，y2x2，归纳总结，课堂小结，随堂训练等内容，欢迎下载使用。

探究二次函数y = ax 2与y=ax2+c的联系．
能够画出二次函数y=ax2+c的图象.
通过观察图象，掌握y=ax2+c的图象特征和性质.（重点）
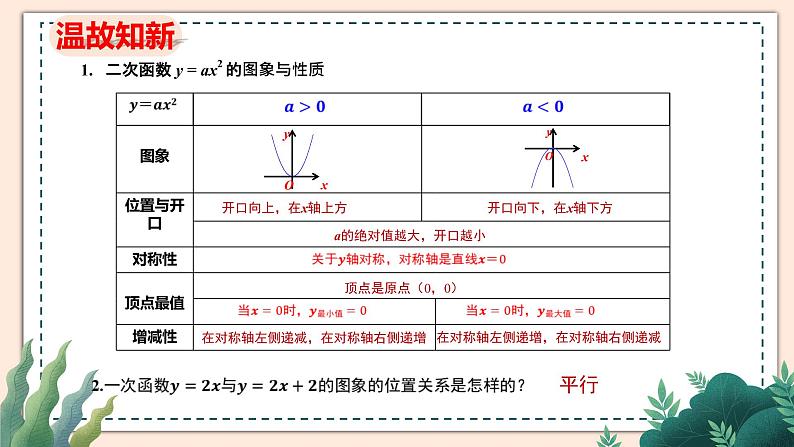
1. 二次函数 y = ax2 的图象与性质　　
a的绝对值越大，开口越小
在对称轴左侧递减，在对称轴右侧递增
在对称轴左侧递增，在对称轴右侧递减
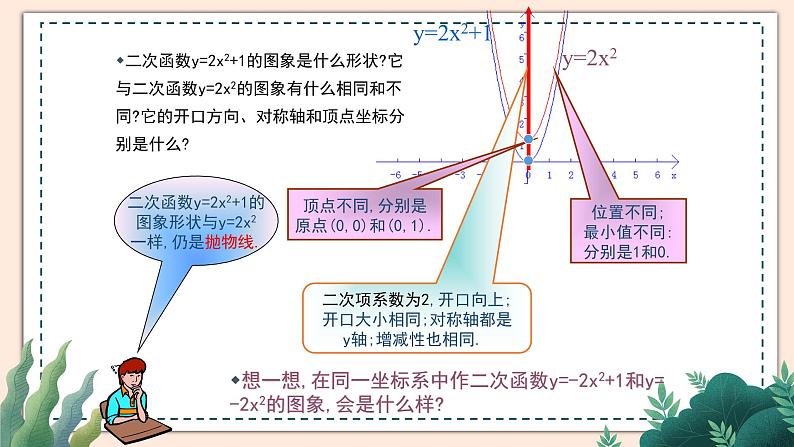
在同一坐标系中作出二次函数y=2x²+1的图象与二次函数y=2x²的图象.
二次函数y=2x²+1的图象与二次函数y=2x²的图象有什么关系?它们是轴对称图形吗?它的开口方向、对称轴和顶点坐标分别是什么?作图看一看．
二次项系数为2,开口向上;开口大小相同;对称轴都是y轴;增减性也相同.
顶点不同,分别是原点(0,0)和(0,1).
二次函数y=2x2+1的图象形状与y=2x2一样,仍是抛物线.
二次函数y=2x2+1的图象是什么形状?它与二次函数y=2x2的图象有什么相同和不同?它的开口方向、对称轴和顶点坐标分别是什么?
位置不同;最小值不同:分别是1和0.
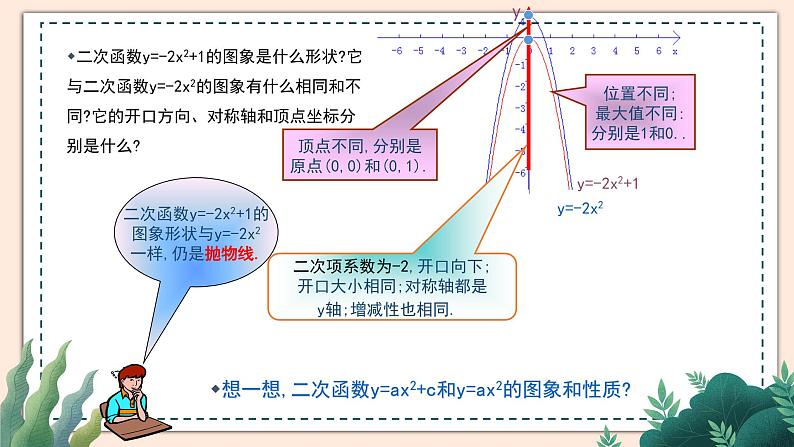
想一想,在同一坐标系中作二次函数y=-2x2+1和y=-2x2的图象,会是什么样?
二次项系数为-2,开口向下;开口大小相同;对称轴都是y轴;增减性也相同.
二次函数y=-2x2+1的图象形状与y=-2x2一样,仍是抛物线.
二次函数y=-2x2+1的图象是什么形状?它与二次函数y=-2x2的图象有什么相同和不同?它的开口方向、对称轴和顶点坐标分别是什么?
位置不同;最大值不同:分别是1和0..
想一想,二次函数y=ax2+c和y=ax2的图象和性质?
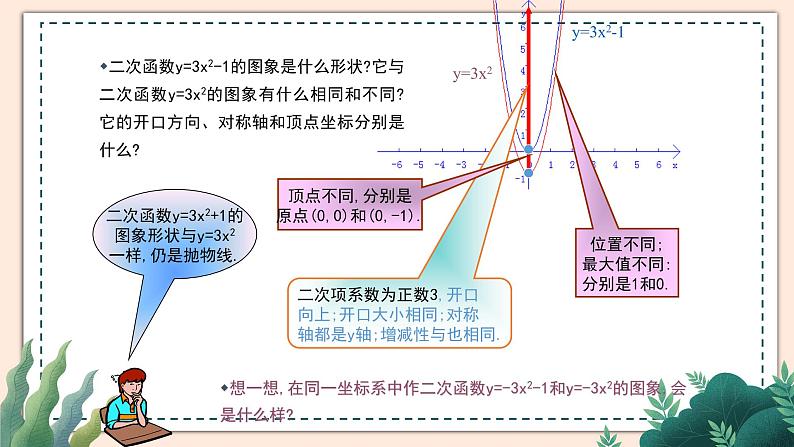
在同一坐标系中作出二次函数y=3x²-1的图象与二次函数y=3x²的图象.
二次函数y=3x² -l的图象与二次函数y=3x²的图象有什么关系?它们是轴对称图形吗?它的开口方向、对称轴和顶点坐标分别是什么?
二次项系数为正数3,开口向上;开口大小相同;对称轴都是y轴;增减性与也相同.
顶点不同,分别是原点(0,0)和(0,-1).
二次函数y=3x2+1的图象形状与y=3x2一样,仍是抛物线.
二次函数y=3x2-1的图象是什么形状?它与二次函数y=3x2的图象有什么相同和不同?它的开口方向、对称轴和顶点坐标分别是什么?
位置不同;最大值不同:分别是1和0.
想一想,在同一坐标系中作二次函数y=-3x2-1和y=-3x2的图象,会是什么样?
二次函数y=-3x2-1的图象是什么形状?它与二次函数y=-3x2的图象有什么相同和不同?它的开口方向、对称轴和顶点坐标分别是什么?
请你总结二次函数y=ax2+c的图象和性质.
二次函数y=ax2+c的图象和性质
y=ax2 +c(a>0)
y=ax2 +c(a<0)
当c>0时,在x轴的上方(经过一,二象限);当c<0时,与x轴相交(经过一,二三四象限).
当c<0时,在x轴的下方(经过三,四象限);当c>0时,与x轴相交(经过一,二三四象限).
当x=0时,最小值为c.
当x=0时,最大值为c.
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
二次函数y=ax²+c与=ax²的关系
1.相同点: (1)图像都是抛物线, 形状相同, 开口方向相同. (2)都是轴对称图形, 对称轴都是y轴.(3)都有最(大或小)值.(4)a>0时, 开口向上,在y轴左侧,y都随x的增大而减小,在y轴右侧,y都随 x的增大而增大. a<0时,开口向下,在y轴左侧,y都随x的增大而增大,在y轴右侧,y都随 x的增大而减小 .
2.不同点:(1)顶点不同:分别是(0,c),(0,0). (2)最值不同:分别是c和0.3.联系: y=ax²+c(a≠0) 的图象可以看成y=ax²的图象沿y轴整体平移|c|个单位得到的.(当c>0时向上平移;当c<0时,向下平移).
关于y轴对称，开口向上
二次函数y=ax2+c的图象的平移
二次函数y=ax2+c的图象可以由 y=ax2 的图象平移得到：
当c> 0 时,向上平移c个单位长度得到；
思考 二次函数 y=ax2 与y=ax2+c（a≠0）的图象有什么关系？
当c＜ 0 时,向下平移-c个单位长度得到；