人教版七年级上册1.3.1 有理数的加法说课ppt课件

这是一份人教版七年级上册1.3.1 有理数的加法说课ppt课件，共27页。PPT课件主要包含了我是火炬手，东East，加数异号，加数的绝对值不相等，相同符号，结果是0，仍是这个数，有理数的加法法则等内容，欢迎下载使用。

1.了解有理数加法的意义，理解有理数加法法则的合理性.Understand the meaning f ratinal number additin and the ratinality f ratinal number additin rules.2.能运用该法则准确进行有理数的加法运算.(重点）Be able t use the additin rules f ratinal numbers accurately.3.探索有理数加法法则的过程，理解并掌握有理数加法的法则.（难点）Explre the prcess f ratinal number additin rule, understand and master the rule f ratinal number additin.
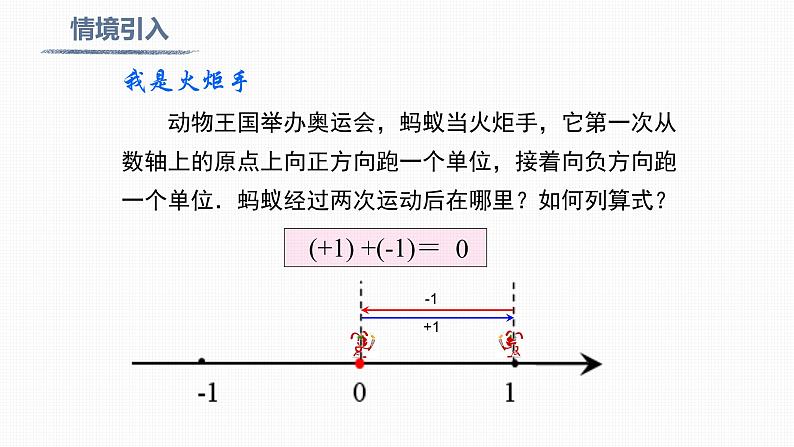
(+1) +(-1)＝
动物王国举办奥运会，蚂蚁当火炬手，它第一次从数轴上的原点上向正方向跑一个单位，接着向负方向跑一个单位．蚂蚁经过两次运动后在哪里？如何列算式？
一只可爱的小狗，在一条东西走向的笔直公路上行走，现规定向东为正，向西为负.A lvely little dg walks n a straight east-west rad. It is nw stipulated that East is psitive and West is negative.
如果小狗先向东行走2米，再继续向东行走1米，则小狗两次一共向哪个方向行走了多少米？If the dg walks 2 meters t the East and then cntinues t walk 1 meter t the East, hw many meters did the dg walk ,in which directin?
解：小狗一共向东行走了（2+1）米，写成算是为：
（+2）+（+1）= +（2+1）（m）
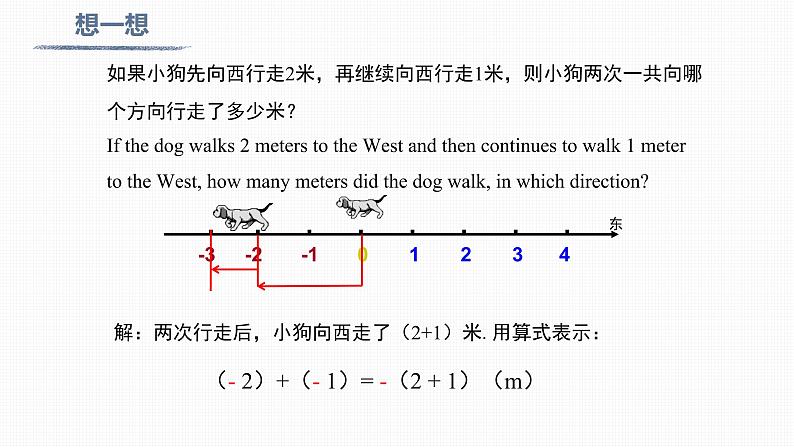
如果小狗先向西行走2米，再继续向西行走1米，则小狗两次一共向哪个方向行走了多少米？If the dg walks 2 meters t the West and then cntinues t walk 1 meter t the West, hw many meters did the dg walk, in which directin?
解：两次行走后，小狗向西走了（2+1）米.用算式表示：
（- 2）+（- 1）= -（2 + 1）（m）
你从上面两个式子中发现了什么？
同号两数相加，取相同的符号，并把绝对值相加.Add tw numbers with the same sign, take the same sign, and add the abslute values.
有理数加法法则一 Ratinal number additin rule 1：
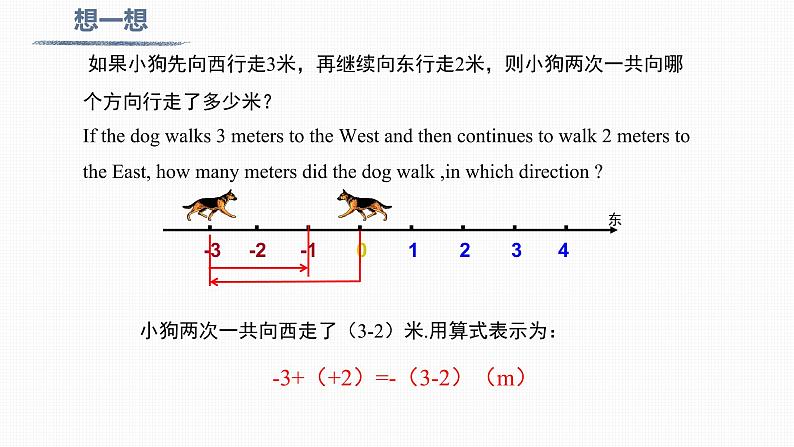
如果小狗先向西行走3米，再继续向东行走2米，则小狗两次一共向哪个方向行走了多少米？If the dg walks 3 meters t the West and then cntinues t walk 2 meters t the East, hw many meters did the dg walk ,in which directin ?
小狗两次一共向西走了（3-2）米.用算式表示为：
-3+（+2）=-（3-2）（m）
如果小狗先向西行走2米，再继续向东行走3米，则小狗两次一共向哪个方向行走了多少米？If the dg walks 2 meters t the West and then cntinues t walk 3 meters t the East, hw many meters did the dg walk in which directin twice?
小狗两次一共向东走了（3-2）米.用算式表示为：
-2+（+3）=+（3-2）（m）
如果小狗先向西行走2米，再继续向东行走2米，则小狗两次一共向哪个方向行走了多少米？If the dg walks 2 meters t the West and then cntinues t walk 2 meters t the East, hw many meters did the dg walk ,in which directin ?
（-2）+（+2）= 0（m）
解：小狗一共行走了0米.写成算式为：
-2 + (+3) = +（3-2） -3 + (+2）= -（3-2） -2 + (+2）= （2-2）
你从上面三个式子中发现了什么？What d yu find frm the abve three frmulas?
有理数加法法则二：Ratinal number additin rule 2
异号两数相加，绝对值相等时和为0；绝对值不相等时，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值.Tw numbers with different signs are added. When the abslute values are equal, the sum is 0; When the abslute values are nt equal, take the sign f the addend with the larger abslute value and subtract the smaller abslute value frm the larger abslute value.
如果小狗先向西行走3米，然后在原地休息，则小狗向哪个方向行走了多少米？If the dg walks 3 meters westward and then rests in place, in which directin did the dg walk ,hw many meters?
小狗向西行走了3米.写成算式为：
（-3）+0= -3（m）
有理数加法法则三：Ratinal number additin rule 3
一个数同0相加，仍得这个数.
有理数加法法则 Ratinal number additin rule
(1)同号两数相加，结果取相同符号，并把绝对值相加．Add tw numbers with the same sign, take the same sign as the result, and add the abslute values.(2)异号两数相加，结果取绝对值较大的加数的符号，并将较大的绝对值减较小的绝对值．互为相反数的两个数相加得0．When tw numbers with different signs are added, the sign f the addend with the larger abslute value is taken, and the larger abslute value is subtracted frm the smaller abslute value. The additin f tw ppsite numbers is 0.(3)一个数同0相加，仍得这个数． The additin f a number and 0 is still this number.
Example 1 Calculate：（1）（－4）＋（－8）；（2）（－5）＋13；（3）0＋（－7）； （4）（－4.7）＋4.7．
Slutin：（1）（－4）＋（－8）　　　 　＝－（4＋8）　　　　 ＝－12 （2）（－5）＋13＝＋（13－5）＝8 （3）0＋（－7）＝－7 （4）（－4.7）＋3.9＝－（4.7-3.9）＝-0.8
互为相反意义的量可以全部抵消或部分抵消．Quantities with ppsite meanings can be cancelled in whle r in part.
通过有理数加法法则的学习，你们认为如何进行有理数加法运算呢？Thrugh the study f ratinal number additin rule, hw d yu think t carry ut ratinal number additin?
方法总结：1.先判断类型（同号、异号等）Judge the type first (same sign, different sign, etc.)；2.再确定和的符号；Then decide the sign f the sum.3.最后进行绝对值的加减运算.Finally, peratins f abslute value.
Example 2 Given that│a│= 8，│b│= 2； （1）When a、b have the same sign,find the value f a+b；（2）When a、b have the different sign,find the value f a+b.
分析：先根据的a、b符号，分类讨论，再计算a+b的值
解：因为│a│= 8，│b│= 2，所以a= ±8，b= ±2.
（1）因为a、b同号，所以a= 8，b= 2或a= -8，b= -2.
所以a+b= 8+2=10，或a+b=- 8+（-2）=-10.
（2）因为a、b异号，所以a= 8，b=- 2或a= -8，b= 2.
所以a+b= 8+（-2）=6，或a+b=- 8+2=-6.
If |x－3| and |y＋2| are ppsite numbers ,find the value f x＋y．
解：由题意得|x－3|+|y＋2|=0，又|x－3|≥0，|y＋2|≥0，所以x－3= 0，y＋2=0，所以x=3 ，y=－2.
所以x＋y=3－2=1.
例3 足球循环赛中，红队胜黄队4:1，黄队胜蓝队1:0，蓝队胜红队1:0，计算各队的净胜球数.Example 3 In the ftball rund rbin match, the red team wins the yellw team by 4:1, the yellw team wins the blue team by 1:0, and the blue team wins the red team by 1:0. Calculate the gals f each team.
每个队的进球总数记为正数，失球总数记为负数，这两数的和为这队的净胜球数.The ttal number f gals scred by each team is recrded as a psitive number and the ttal number f gals lst is recrded as a negative number. The sum f these tw numbers is the team's gal.三场比赛中，红队共进4球，失2球，净胜球数为In the three games, the red team scred 4 gals, lst 2 gals and had a win f（＋4）＋（－2）＝＋（4－2）＝2黄队共进2球，失4球，净胜球为 The yellw team scred 2 gals, lst 4 gals and had a win f（＋2）＋（－4）＝－（4－2）＝－2篮球共进（ ）球，失（ ）球，净胜球数为The blue team scred ( ) gals, lst ( ) gals and had a win f（ ）.
（＋1）＋（－1）＝0
海平面的高度为0m.一艘潜艇从海平面先下潜40m,再上升15m.求现在这艘潜艇相对于海平面的位置.（上升为正，下潜为负）The height f the sea level is 0m. A submarine dives 40m frm the sea level and then rises 15m. Find the current psitin f the submarine relative t the sea level. (rising is psitive and diving is negative)
解：潜水艇下潜40m,记作-40m;上升 15m,记作+15m.根据题意，得（-40）+（+15）=-（40-25）=-25（m)答：现在这艘潜艇位于海平面下25m处.
1.两个有理数的和为零，则这两个有理数一定（ ） A.都是零 B.至少有一个是零 C.一正一负 D.互为相反数2.在1，－1，-2这三个数中，任意两数之和的最大值是（ ） A.1 B.0 C.-1 D.3
A. a+c＜0 B. b+c＜0 C. -b+a＜0 D.-a+b+c＜0
3.已知有理数a,b,c在数轴上的位置如图所示，则下列结论中错误的是（ ）
A.1 B.－5 C.－5或－1 D.5或1
4.若│x│= 3，│y│= 2，且x>y，则x+y的值为（ ）
(1)(-0.6)+(-2.7)；   (2)3.7+(-8.4)； (3)3.22+1.78； (4)7+(-3.3). 
答案：(1)-3.3 (2)-4.7 (3)5 (4)3.7
解：中午的气温为-25+11=-14（℃）， 夜间的气温为-14+（-13）=-27（℃）
6.某城市一天早晨的气温是-25℃，中午上升了11℃，夜间又下降了13℃，那么这天中午、夜间的气温分别是多少？
取绝对值较大的加数的符号