
高中数学8.1 基本立体图形第2课时导学案
展开8.1 第2课时 圆柱、圆锥、圆台、球、简单组合体的结构特征
【学习目标】
素 养 目 标 | 学 科 素 养 |
1.几何体的结构特征,能够识别和区分这些几何体 2.会根据旋转体的几何体特征进行相关运算 3.会根据旋转体的几何体特征进行相关运算 | 1.数学运算; 2.直观想象 |
【自主学习】
一.圆柱的结构特征
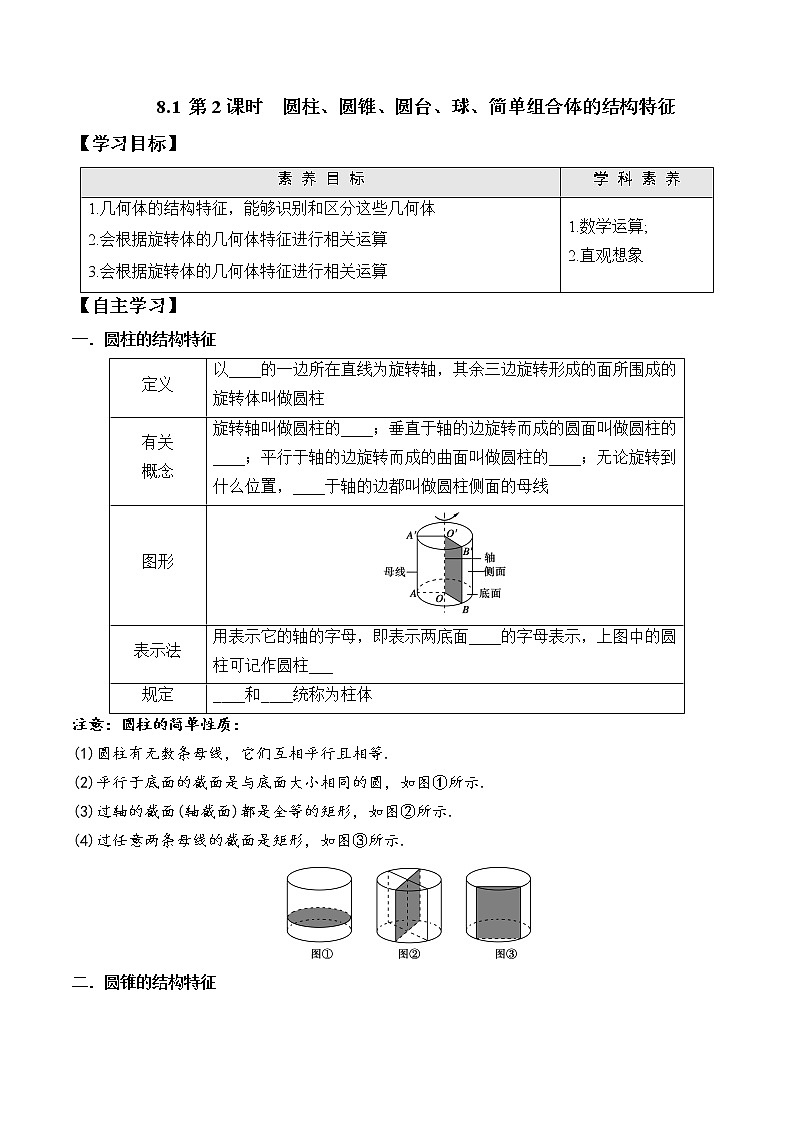
定义 | 以____的一边所在直线为旋转轴,其余三边旋转形成的面所围成的旋转体叫做圆柱 |
有关 概念 | 旋转轴叫做圆柱的____;垂直于轴的边旋转而成的圆面叫做圆柱的____;平行于轴的边旋转而成的曲面叫做圆柱的____;无论旋转到什么位置,____于轴的边都叫做圆柱侧面的母线 |
图形 | |
表示法 | 用表示它的轴的字母,即表示两底面____的字母表示,上图中的圆柱可记作圆柱___ |
规定 | _ _和_ _统称为柱体 |
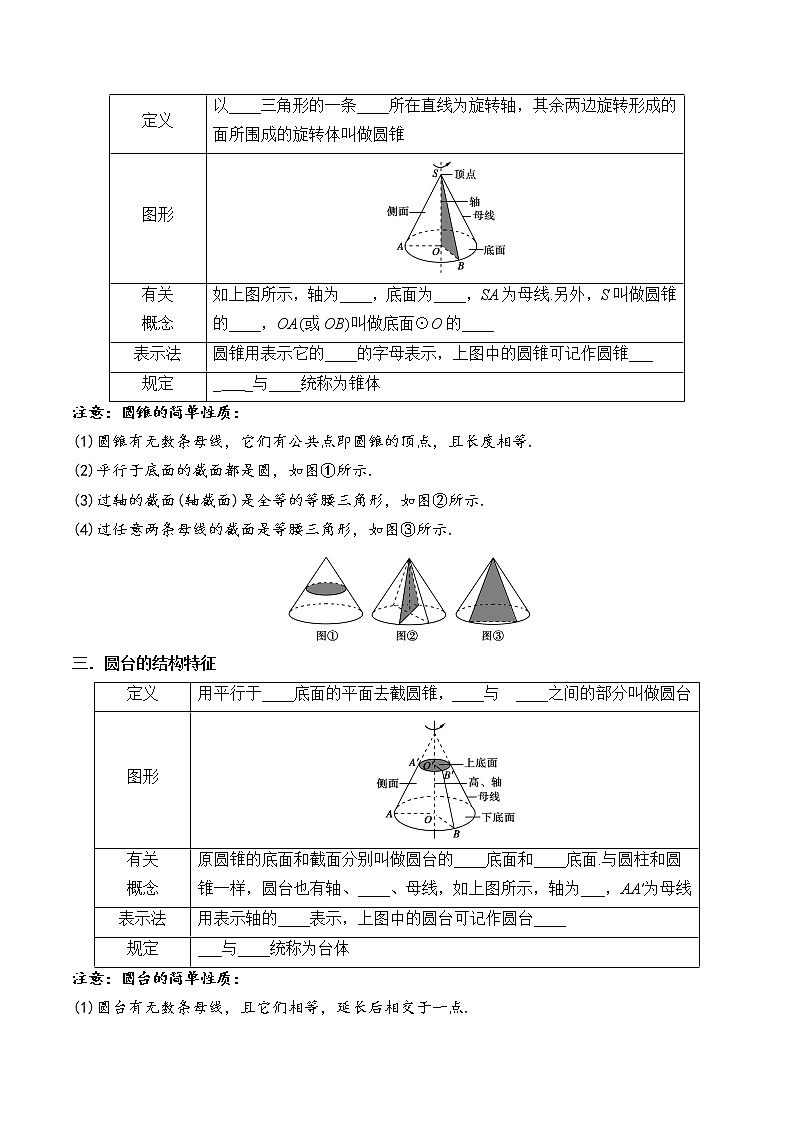
注意:圆柱的简单性质:
(1)圆柱有无数条母线,它们互相平行且相等.
(2)平行于底面的截面是与底面大小相同的圆,如图①所示.
(3)过轴的截面(轴截面)都是全等的矩形,如图②所示.
(4)过任意两条母线的截面是矩形,如图③所示.
二.圆锥的结构特征
定义 | 以____三角形的一条____所在直线为旋转轴,其余两边旋转形成的面所围成的旋转体叫做圆锥 |
图形 | |
有关 概念 | 如上图所示,轴为____,底面为____,SA为母线.另外,S叫做圆锥的____,OA(或OB)叫做底面⊙O的____ |
表示法 | 圆锥用表示它的____的字母表示,上图中的圆锥可记作圆锥___ |
规定 | _ _与____统称为锥体 |
注意:圆锥的简单性质:
(1)圆锥有无数条母线,它们有公共点即圆锥的顶点,且长度相等.
(2)平行于底面的截面都是圆,如图①所示.
(3)过轴的截面(轴截面)是全等的等腰三角形,如图②所示.
(4)过任意两条母线的截面是等腰三角形,如图③所示.
三.圆台的结构特征
定义 | 用平行于____底面的平面去截圆锥,____与 ____之间的部分叫做圆台 |
图形 | |
有关 概念 | 原圆锥的底面和截面分别叫做圆台的____底面和____底面.与圆柱和圆锥一样,圆台也有轴、____、母线,如上图所示,轴为___,AA′为母线 |
表示法 | 用表示轴的____表示,上图中的圆台可记作圆台____ |
规定 | ___与____统称为台体 |
注意:圆台的简单性质:
(1)圆台有无数条母线,且它们相等,延长后相交于一点.
(2)平行于底面的截面是圆,如图①所示.
(3)过轴的截面是全等的等腰梯形,如图②所示.
(4)过任意两条母线的截面是等腰梯形,如图③所示.
四.球
定义 | 以半圆的____所在直线为旋转轴,半圆面旋转____形成的旋转体叫做球体,简称球 |
有关 概念 | 半圆的__ __叫做球的球心;半圆的____叫做球的半径;半圆的___叫做球的直径 |
图形 | |
表示法 | 球常用表示____的字母表示,如上图中的球记作球___ |
五.简单组合体
(1)概念:由 组合而成的几何体叫做简单组合体.
(2)两种构成形式
①由简单几何体 而成;
②由简单几何体 一部分而成.
【小试牛刀】
1.思维辨析(对的打“√”,错的打“×”)
(1)半圆绕其直径所在直线旋转一周形成球.( )
(2)夹在圆柱的两个平行截面间的几何体是一圆柱.( )
(3)直角三角形绕一边所在直线旋转得到的旋转体是圆锥.( )
(4)圆柱、圆锥、圆台的底面都是圆面.( )
2.可以旋转得到如图的图形的是( )
3.过圆锥的轴作截面,则截面形状一定是( )
A.直角三角形 B.等腰三角形
C.等边三角形 D.等腰直角三角形
【经典例题】
题型一 旋转体的结构特征
点拨:简单旋转体判断问题的解题策略
1.准确掌握圆柱、圆锥、圆台和球的生成过程及其特征性质是解决此类概念问题的关键;
2.解题时要注意两个明确:,①明确由哪个平面图形旋转而成;,②明确旋转轴是哪条直线.
例1 下列结论正确的是____.
①以直角三角形的一边为轴旋转一周所得的旋转体是圆锥;
②以直角梯形的一腰为轴旋转一周所得的旋转体是圆台;
③圆柱、圆锥、圆台的底面都是圆;
④以等腰三角形的底边上的高所在的直线为旋转轴,其余各边旋转一周形成的曲面围成的几何体是圆锥;
⑤球面上四个不同的点一定不在同一平面内;
⑥球的半径是球面上任意一点和球心的连线段;
⑦球面上任意三点可能在一条直线上;
⑧用一个平面去截球,得到的截面是一个圆面.
【跟踪训练】1下列命题:①任意平面截圆柱,截面都是圆面;②圆锥的顶点与底面圆周上任意一点的连线是圆锥的母线;③在圆台上、下两底面的圆周上各取一点,则这两点的连线是圆台的母线,其中正确的是( )
A.①② B.②③ C.①③ D.②
题型二 简单组合体的结构特征
例2 如图所示的几何体是由下面哪一个平面图形旋转而形成的( )
【跟踪训练】2已知AB是直角梯形ABCD中与底边垂直的腰,如图所示.分别以AB,BC,CD,DA所在的直线为轴旋转,试说明所得几何体的结构特征.
题型三 圆柱、圆锥、圆台的计算问题
点拨:旋转体中有关底面半径、母线、高的计算,可利用轴截面求解,借助直角三角形或三角形的相似关系建立高、母线长、底面圆的半径长的等量关系,即将立体问题平面化.对于圆台的轴截面,可将两腰延长相交后在三角形中求解.这是解答圆台问题常用的方法.
例3 已知一个圆台的母线长为12 cm,两底面的面积分别为4π cm2和25π cm2,求:
(1)圆台的高;
(2)截得此圆台的圆锥的母线长.
【跟踪训练】3如图所示,用一个平行于圆锥SO底面的平面截这个圆锥,截得圆台上、下底面的面积之比为1∶16,截去的圆锥的母线长是3 cm,求圆台O′O的母线长.
题型四 球的截面问题
点拨:利用球的截面,借助直角三角形,将立体问题转化为平面问题是解决球的有关问题的关键.
例4 已知半径为10的球的两个平行截面的周长分别是12π和16π,求这两个截面间的距离.
【跟踪训练】4 一个与球心距离为1的平面截球所得的圆面面积为π,则球的直径为 .
【当堂达标】
1.如图所示的图形中有( )
A.圆柱、圆锥、圆台和球 B.圆柱、球和圆锥
C.球、圆柱和圆台 D.棱柱、棱锥、圆锥和球
2.如图所示的组合体的结构特征是( )
A.一个棱柱中截去一个棱柱
B.一个棱柱中截去一个圆柱
C.一个棱柱中截去一个棱锥
D.一个棱柱中截去一个棱台
3.下列说法中正确的是________.
①连接圆柱上、下底面圆周上两点的线段是圆柱的母线;
②圆锥截去一个小圆锥后剩余部分是圆台;
③通过圆台侧面上一点,有无数条母线.
4.若母线长是4的圆锥的轴截面的面积是8,则该圆锥的高是________.
5.一个圆台上、下底面的半径分别为3 cm和8 cm,若两底面圆心的连线长为12 cm,则这个圆台的母线长为________cm.
6.指出图中的三个几何体分别是由哪些简单几何体组成的.
【课堂小结】
1.圆柱、圆锥、圆台的关系如图所示.
2.处理台体问题常采用还台为锥的补体思想.
3.处理组合体问题常采用分割思想.
4.重视圆柱、圆锥、圆台的轴截面在解决几何量中的特殊作用,切实体会空间几何平面化的思想.
【参考答案】
【自主学习】
矩形 轴 底面 侧面 平行 圆心 O′O 圆柱 棱柱
直角 直角边 SO ⊙O 顶点 半径 轴 SO 棱锥 圆锥
圆锥 底面 截面 下 上 侧面 OO′ 字母 OO′ 圆台 棱台
直径 一周 圆心 半径 直径 球心 O
简单几何体 拼接 截去或挖去
【小试牛刀】
1.(1)× (2)× (3)× (4)√
2.A 解析:题图所示几何体上面是圆锥,下面是圆台,故平面图形应是由一个直角三角形和一个直角梯形构成.
3.B
【经典例题】
例1 ④⑥⑧ 解析:①以直角三角形的一条直角边为轴旋转一周才可以得到圆锥;②以直角梯形垂直于底边的一腰为轴旋转一周可得到圆台;③它们的底面为圆面;④正确;作球的一个截面,在截面的圆周上任意取四点,则这四点就在球面上,故⑤错误;根据球的半径定义可知⑥正确;球面上任意三点一定不共线,故⑦错误;用一个平面去截球,一定截得一个圆面,故⑧正确.
【跟踪训练】1 D 解析:过圆柱两母线的截面为矩形,有时斜的截面为椭圆,故①错误;圆台的母线不是上底面和下底面上任意两点的连线,③错误;由圆锥母线的定义知②正确.
例2 A 解析:该几何体自上而下由圆锥、圆台、圆台、圆柱组合而成,故应选A.
【跟踪训练】2 解:(1)以AB边所在的直线为轴旋转所得旋转体是圆台,如图①所示.
(2)以BC边所在的直线为轴旋转所得旋转体是一个组合体:下部为圆柱,上部为圆锥,如图②所示.
(3)以CD边所在的直线为轴旋转所得旋转体为一个组合体:上部为圆锥,下部为圆台,再挖去一个小圆锥,如图③所示.
(4)以AD边所在的直线为轴旋转所得旋转体是一个组合体:一个圆柱上部挖去一个圆锥,如图④所示.
例3 [解] (1)设圆台的轴截面为等腰梯形ABCD(如图所示).
由题意可得上底的一半O1A=2 cm,下底的一半OB=5 cm,腰长AB=12 cm,所以圆台的高AM==3(cm).
(2)如图,延长BA,OO1,CD,交于点S,设截得此圆台的圆锥的母线长为l cm,
则由△SAO1∽△SBO,得=,解得l=20.故截得此圆台的圆锥的母线长为20 cm.
【跟踪训练】3【解】 设圆台的母线长为l cm,
由截得的圆台上、下底面面积之比为1∶16,可设
截得的圆台的上、下底面的半径分别为r cm,4r cm.过轴SO作截面,如图所示,
则△SO′A′∽△SOA,SA′=3 cm.
所以=,所以==.
解得l=9,即圆台O′O的母线长为9 cm.
例4 [解] 设球的大圆为圆O,C,D两点为两截面圆的圆心,AB为经过C,O,D三点的直径且两截面圆的半径分别是6和8.
当两截面在球心同侧时,如图(1),此时CD=OC-OD=-=8-6=2.
当两截面在球心两侧时,如图(2),此时CD=OC+OD=+=8+6=14.
故两截面间的距离为2或14.
【跟踪训练】4 2解析:设球心到平面的距离为d,截面圆的半径为r,则πr2=π,∴r=1,
设球的半径为R,则R==,故球的直径为2.
【当堂达标】
1.B 解析:根据题中图形可知,(1)是球,(2)是圆柱,(3)是圆锥,(4)不是圆台,故应选B.
2.C 解析:如题图,可看成是四棱柱截去一个角,即截去一个三棱锥后得到的简单组合体,故为一个棱柱中截去一个棱锥所得.
3. ② 解析:①错误,连接圆柱上、下底面圆周上两点的线段不一定与圆柱的轴平行,所以①不正确.③错误,通过圆台侧面上一点,只有一条母线.
4. 2 解析:设圆锥的底面半径为r,则圆锥的高h= .
由题意可知·2r·h=r=8,所以r2=8,所以h=2.
5. 13 解析:如图,过点A作AC⊥OB,交OB于点C.在Rt△ABC中,AC=12 cm,BC=8-3=5 (cm).所以AB==13(cm).
6.解:(1)几何体由一个圆锥、一个圆柱和一个圆台拼接而成.
(2)几何体由一个六棱柱和一个圆柱拼接而成.
(3)几何体由一个球和一个圆柱中挖去一个以圆柱下底面为底面、上底面圆心为顶点的圆锥拼接而成.
高中人教A版 (2019)8.3 简单几何体的表面积与体积导学案: 这是一份高中人教A版 (2019)8.3 简单几何体的表面积与体积导学案,共7页。学案主要包含了学习目标,自主学习,经典例题,跟踪训练,当堂达标,参考答案等内容,欢迎下载使用。
高中数学人教A版 (2019)必修 第二册8.1 基本立体图形第2课时学案及答案: 这是一份高中数学人教A版 (2019)必修 第二册8.1 基本立体图形第2课时学案及答案,共8页。学案主要包含了探索新知等内容,欢迎下载使用。
高中数学8.1 基本立体图形第2课时导学案: 这是一份高中数学8.1 基本立体图形第2课时导学案