



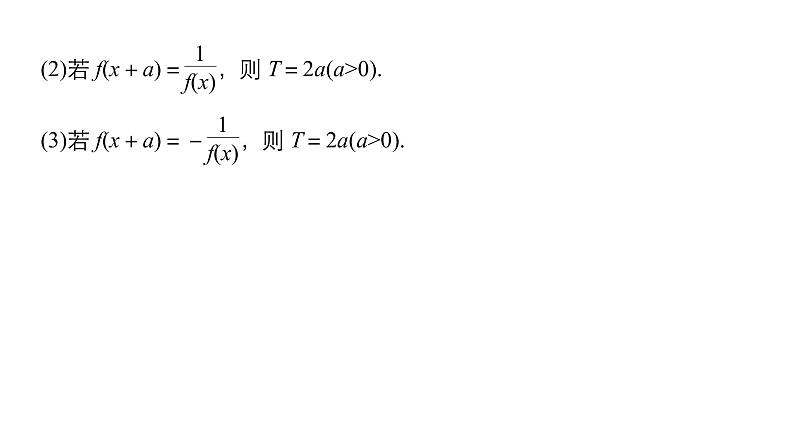



人教A版 (2019)必修 第一册5.4 三角函数的图象与性质教学课件ppt
展开f(-x)=-f(x)
2.周期性(1)周期函数:对于函数y=f(x),如果存在一个非零常数T,使得当x取定义域内的任何值时,都有 ,那么就称函数y=f(x)为周期函数,称T为这个函数的周期.(2)最小正周期:如果在周期函数f(x)的所有周期中存在一个 的正数,那么这个 就叫做f(x)的最小正周期.
f(x+T)=f(x)
1.函数奇偶性常用结论(1)如果函数f(x)是偶函数,那么f(x)=f(|x|).(2)奇函数在两个对称的区间上具有相同的单调性;偶函数在两个对称的区间上具有相反的单调性.(3)在公共定义域内有:奇±奇=奇,偶±偶=偶,奇×奇=偶,偶×偶=偶,奇×偶=奇.2.函数周期性常用结论对f(x)定义域内任一自变量的值x:(1)若f(x+a)=-f(x),则T=2a(a>0).
题组一 思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)偶函数图象不一定过原点,奇函数的图象一定过原点.( )(2)若函数y=f(x+a)是偶函数,则函数y=f(x)关于直线x=a对称.( )(3)函数f(x)在定义域上满足f(x+a)=-f(x),则f(x)是周期为2a(a>0)的周期函数.( )(4)定义域关于原点对称是函数具有奇偶性的一个必要条件.( )(5)若T是函数的一个周期,则nT(n∈Z,n≠0)也是函数的周期.( )
题组二 教材改编2.[P39A组T6]已知函数f(x)是定义在R上的奇函数,且当x>0时,f(x)=x(1+x),则f(-1)=_____.
解析 f(1)=1×2=2,又f(x)为奇函数,∴f(-1)=-f(1)=-2.
4.[P39A组T6]设奇函数f(x)的定义域为[-5,5],若当x∈[0,5]时,f(x)的图象如图所示,则不等式f(x)<0的解集为______________.
解析 由图象可知,当0<x<2时,f(x)>0;当2<x≤5时,f(x)<0,又f(x)是奇函数,∴当-2<x<0时,f(x)<0,当-5≤x<-2时,f(x)>0.综上,f(x)<0的解集为(-2,0)∪(2,5].
(-2,0)∪(2,5]
解析 依题意得f(-x)=f(x),∴b=0,又a-1=-2a,
题组三 易错自纠5.已知f(x)=ax2+bx是定义在[a-1,2a]上的偶函数,那么a+b的值是
6.偶函数y=f(x)的图象关于直线x=2对称,f(3)=3,则f(-1)=______.
解析 ∵f(x)为偶函数,∴f(-1)=f(1).又f(x)的图象关于直线x=2对称,∴f(1)=f(3).∴f(-1)=3.
典例 判断下列函数的奇偶性:
题型一 判断函数的奇偶性
∴f(-x)=-f(x)且f(-x)=f(x),∴函数f(x)既是奇函数又是偶函数.
∴函数f(x)为奇函数.
解 显然函数f(x)的定义域为(-∞,0)∪(0,+∞),关于原点对称.∵当x<0时,-x>0,则f(-x)=-(-x)2-x=-x2-x=-f(x);当x>0时,-x<0,则f(-x)=(-x)2-x=x2-x=-f(x);综上可知:对于定义域内的任意x,总有f(-x)=-f(x),∴函数f(x)为奇函数.
判断函数的奇偶性,其中包括两个必备条件:(1)定义域关于原点对称,这是函数具有奇偶性的必要不充分条件,所以首先考虑定义域;(2)判断f(x)与f(-x)是否具有等量关系.在判断奇偶性的运算中,可以转化为判断奇偶性的等价关系式f(x)+f(-x)=0(奇函数)或f(x)-f(-x)=0(偶函数)是否成立.
跟踪训练 (1)下列函数中,既不是奇函数,也不是偶函数的是A.y=x+sin 2x B.y=x2-cs xC.y=2x+ D.y=x2+sin x
解析 对于A,f(-x)=-x+sin 2(-x)=-(x+sin 2x)=-f(x),为奇函数;对于B,f(-x)=(-x)2-cs(-x)=x2-cs x=f(x),为偶函数;
对于D,y=x2+sin x既不是偶函数也不是奇函数.
(2)函数f(x)=lg|sin x|是A.最小正周期为π的奇函数B.最小正周期为2π的奇函数C.最小正周期为π的偶函数D.最小正周期为2π的偶函数
解析 易知函数的定义域为{x|x≠kπ,k∈Z},关于原点对称,又f(-x)=lg|sin(-x)|=lg|-sin x|=lg|sin x|=f(x),所以f(x)是偶函数,又函数y=|sin x|的最小正周期为π,所以函数f(x)=lg|sin x|是最小正周期为π的偶函数.
题型二 函数的周期性及其应用
解析 由于函数f(x)是周期为4的奇函数,
2.(2017·山东)已知f(x)是定义在R上的偶函数,且f(x+4)=f(x-2).若当x∈[-3,0]时,f(x)=6-x,则f(919)=_____.
解析 ∵f(x+4)=f(x-2),∴f((x+2)+4)=f((x+2)-2),即f(x+6)=f(x),∴f(x)是周期为6的周期函数,∴f(919)=f(153×6+1)=f(1).又f(x)是定义在R上的偶函数,∴f(1)=f(-1)=6,即f(919)=6.
3.定义在R上的函数f(x)满足f(x+6)=f(x),当-3≤x<-1时,f(x)=-(x+2)2;当-1≤x<3时,f(x)=x.则f(1)+f(2)+f(3)+…+f(2 018)=_____.
解析 ∵f(x+6)=f(x),∴周期T=6.∵当-3≤x<-1时,f(x)=-(x+2)2;当-1≤x<3时,f(x)=x,∴f(1)=1,f(2)=2,f(3)=f(-3)=-1,f(4)=f(-2)=0,f(5)=f(-1)=-1,f(6)=f(0)=0,∴f(1)+f(2)+…+f(6)=1,∴f(1)+f(2)+f(3)+…+f(2 015)+f(2 016)=1× =336.又f(2 017)=f(1)=1,f(2 018)=f(2)=2,∴f(1)+f(2)+f(3)+…+f(2 018)=339.
函数的周期性反映了函数在整个定义域上的性质.对函数周期性的考查,主要涉及函数周期性的判断,利用函数周期性求值.
命题点1 求函数值或函数解析式
题型三 函数性质的综合应用
典例 (1)(2017·全国Ⅱ)已知函数f(x)是定义在R上的奇函数,当x∈(-∞,0)时,f(x)=2x3+x2,则f(2)=_____.
解析 方法一 令x>0,则-x<0.∴f(-x)=-2x3+x2.∵函数f(x)是定义在R上的奇函数,∴f(-x)=-f(x).∴f(x)=2x3-x2(x>0).∴f(2)=2×23-22=12.方法二 f(2)=-f(-2)=-[2×(-2)3+(-2)2]=12.
(2)(2016·全国Ⅲ改编)已知f(x)为偶函数,当x≤0时,f(x)=e-x-1-x,则f(x)=___________________.
解析 ∵当x>0时,-x<0,∴f(x)=f(-x)=ex-1+x,
典例 (1)设函数f(x)= 为奇函数,则k=____.
解析 ∵f(x)为奇函数,∴f(-x)=-f(x),
∴(x+2)(x+k)=(2-x)(k-x),x2+2x+kx+2k=2k-kx-2x+x2,∴k=-2.
解析 因为f(x)是定义在R上且周期为2的函数,
即3a+2b=-2. ①
由①②得a=2,b=-4,从而a+3b=-10.
命题点3 利用函数的性质解不等式
典例 (1)已知定义在R上的偶函数f(x),对任意x1,x2∈[0,+∞)(x1≠x2),有 <0,则A.f(3)
(-∞,-2)∪(2,+∞)
∴x·f(x)<0的解集为(-∞,-2)∪(2,+∞).
∵f(x)为奇函数,在(-∞,0)上是减函数,f(-2)=0,
(1)关于奇偶性、单调性、周期性的综合性问题,关键是将未知区间上的问题转化为已知区间上的问题.(2)掌握以下两个结论,会给解题带来方便:①f(x)为偶函数⇔f(x)=f(|x|).②若奇函数在x=0处有意义,则f(0)=0.
跟踪训练 (1)已知f(x)是定义在R上的奇函数,且在[0,+∞)上单调递增,若f(lg x)<0,则x的取值范围是A.(0,1) B.(1,10)C.(1,+∞) D.(10,+∞)
解析 由题意,函数f(x)在R上是增函数,且f(0)=0,不等式f(lg x)<0=f(0)等价于lg x<0,故0
一、函数性质的判断典例1 (1)(2017·北京)已知函数f(x)=3x- ,则f(x)A.是偶函数,且在R上是增函数B.是奇函数,且在R上是增函数C.是偶函数,且在R上是减函数D.是奇函数,且在R上是减函数
解析 ∵函数f(x)的定义域为R,
∴函数f(x)是奇函数.
又∵y=3x在R上是增函数,
(2)(2017·荆州模拟)下列函数:①y=sin3x+3sin x;
其中是奇函数且在(0,1)上是减函数的个数为A.1 B.2 C.3 D.4
解析 易知①中函数在(0,1)上为增函数;④中函数不是奇函数;满足条件的函数为②③.
(3)定义在实数集R上的函数f(x)满足f(x)+f(x+2)=0,且f(4-x)=f(x).现有以下三个命题:①8是函数f(x)的一个周期;②f(x)的图象关于直线x=2对称;③f(x)是偶函数.其中正确命题的序号是________.
解析 由f(x)+f(x+2)=0可得f(x+4)=-f(x+2)=f(x),∴函数f(x)的周期是4,①对;由f(4-x)=f(x),可得f(2+x)=f(2-x),f(x)的图象关于直线x=2对称,②对;f(4-x)=f(-x)且f(4-x)=f(x),∴f(-x)=f(x),f(x)为偶函数,③对.
二、函数性质的综合应用典例2 (1)已知f(x)是定义在R上的奇函数,对任意的实数x,f(x-2)=f(x+2),当x∈(0,2)时,f(x)=-x2,则 等于
解析 由f(x-2)=f(x+2),可知函数f(x)的最小正周期T=4,又由于该函数是奇函数,
(2)函数f(x)= 在[1,+∞)上是增函数,则a的取值范围是___________.
解析 由已知函数y=x+2 018- 在[1,+∞)上是增函数,且y>0恒成立.
[-1,2 019)
∴a≥-1.又由当x=1时,y=1+2 018-a>0,得a<2 019.∴a的取值范围是[-1,2 019) .
(3)已知f(x)是定义在R上的偶函数,且在区间(-∞,0)上单调递增.若实数a满足f(2|a-1|)>f( ),则a的取值范围是________.
又由已知可得f(x)在(0,+∞)上单调递减,
1.下列函数为偶函数的是A.f(x)=x-1 B.f(x)=x2+xC.f(x)=2x-2-x D.f(x)=2x+2-x
解析 函数f(x)=x-1和f(x)=x2+x既不是偶函数也不是奇函数,排除选项A和B;选项C中,f(x)=2x-2-x,则f(-x)=2-x-2x=-f(x),且定义域为R,所以f(x)=2x-2-x为奇函数,排除选项C;选项D中,f(x)=2x+2-x,则f(-x)=2-x+2x=f(x),所以f(x)=2x+2-x为偶函数,故选D.
2.设函数f(x)=ln(1+x)-ln(1-x),则f(x)是A.奇函数,且在(0,1)上是增函数B.奇函数,且在(0,1)上是减函数C.偶函数,且在(0,1)上是增函数D.偶函数,且在(0,1)上是减函数
解析 易知函数定义域为(-1,1),f(-x)=ln(1-x)-ln(1+x)=-f(x),故函数f(x)为奇函数,
由复合函数单调性判断方法知,f(x)在(0,1)上是增函数,故选A.
3.(2017·江西南城一中模拟)已知R上的奇函数f(x)满足:当x>0时,f(x)=x2+x-1,则f(f(-1))等于A.-1 B.1 C.2 D.-2
解析 ∵y=f(x)是奇函数,∴f(-1)=-f(1)=-1,∴f (f(-1) )=f(-1)=-1.
4.已知函数f(x)是定义在R上的奇函数,其最小正周期为4,且当x∈ 时,f(x)=lg2(-3x+1),则f(2 021)等于A.4 B.2 C.-2 D.lg27
解析 ∵函数f(x)是定义在R上的奇函数,其最小正周期为4,∴f(2 021)=f(4×505+1)=f(1)=-f(-1).
f(x)=lg2(-3x+1),∴f(-1)=lg2[-3×(-1)+1]=2,∴f(2 021)=-f(-1)=-2.
5.若f(x)=ex-ae-x为奇函数,则f(x-1)<e- 的解集为A.(-∞,2) B.(-∞,1)C.(2,+∞) D.(1,+∞)
解析 因为f(x)=ex-ae-x为奇函数,所以f(0)=1-a=0,即a=1,则f(x)=ex-e-x在R上单调递增,
6.已知偶函数f(x)对于任意x∈R都有f(x+1)=-f(x),且f(x)在区间[0,1]上是单调递增的,则f(-6.5),f(-1),f(0)的大小关系是A.f(0)<f(-6.5)<f(-1)B.f(-6.5)<f(0)<f(-1)C.f(-1)<f(-6.5)<f(0)D.f(-1)<f(0)<f(-6.5)
解析 由f(x+1)=-f(x),得f(x+2)=-f(x+1)=f(x),∴函数f(x)的周期是2.∵函数f(x)为偶函数,∴f(-6.5)=f(-0.5)=f(0.5),f(-1)=f(1).∵f(x)在区间[0,1]上是单调递增的,∴f(0)<f(0.5)<f(1),即f(0)<f(-6.5)<f(-1).
7.若f(x)=ln(e3x+1)+ax是偶函数,则a=______.
解析 函数f(x)=ln(e3x+1)+ax是偶函数,故f(-x)=f(x),即ln(e-3x+1)-ax=ln(e3x+1)+ax,
整理得e3x+1=e2ax+3x(e3x+1),所以2ax+3x=0,
8.已知函数f(x)在R上为奇函数,且当x>0时,f(x)= +1,则当x<0时,f(x)=____________.
9.设定义在R上的函数f(x)同时满足以下条件:①f(x)+f(-x)=0;②f(x)=f(x+2);③当0≤x≤1时,f(x)=2x-1,则 =_____.
解析 依题意知:函数f(x)为奇函数且周期为2,
= -1+21-1+20-1
10.若函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上是单调递增函数.如果实数t满足f(ln t)+f ≤2f(1),那么t的取值范围是_______.
解析 由于函数f(x)是定义在R上的偶函数,
得f(ln t)≤f(1).又函数f(x)在区间[0,+∞)上是单调递增函数,所以|ln t|≤1,即-1≤ln t≤1,故 ≤t≤e.
11.已知函数f(x)= 是奇函数.(1)求实数m的值;
解 设x<0,则-x>0,所以f(-x)=-(-x)2+2(-x)=-x2-2x.又f(x)为奇函数,所以f(-x)=-f(x).于是x<0时,f(x)=x2+2x=x2+mx,所以m=2.
(2)若函数f(x)在区间[-1,a-2]上单调递增,求实数a的取值范围.
解 要使f(x)在[-1,a-2]上单调递增,
所以1
解 ∵f(1+x)=f(1-x),∴f(-x)=f(2+x).又f(x+2)=f(x),∴f(-x)=f(x).又f(x)的定义域为R,∴f(x)是偶函数.
(2)试求出函数f(x)在区间[-1,2]上的表达式.
解 当x∈[0,1]时,-x∈[-1,0],则f(x)=f(-x)=x;从而当1≤x≤2时,-1≤x-2≤0,f(x)=f(x-2)=-(x-2)=-x+2.
即函数f(x)的周期是4,所以f(2 019)=f(505×4-1)=f(-1).因为函数f(x)为偶函数,所以f(2 019)=f(-1)=f(1).
由f(x)>0,得f(1)=1,所以f(2 019)=f(1)=1.
14.设函数f(x)是定义在R上的偶函数,且对任意的x∈R恒有f(x+1)=f(x-1),已知当x∈[0,1]时,f(x)=2x,则有①2是函数f(x)的周期;②函数f(x)在(1,2)上是减函数,在(2,3)上是增函数;③函数f(x)的最大值是1,最小值是0.其中所有正确命题的序号是________.
解析 在f(x+1)=f(x-1)中,令x-1=t,则有f(t+2)=f(t),因此2是函数f(x)的周期,故①正确;当x∈[0,1]时,f(x)=2x是增函数,根据函数的奇偶性知,f(x)在[-1,0]上是减函数,根据函数的周期性知,函数f(x)在(1,2)上是减函数,在(2,3)上是增函数,故②正确;由②知,f(x)在[0,2]上的最大值f(x)max=f(1)=2,f(x)的最小值f(x)min=f(0)=f(2)=20=1且f(x)是周期为2的周期函数,∴f(x)的最大值是2,最小值是1,故③错误.
15.(2017·东北四市联考)已知f(x)是R上最小正周期为2的周期函数,且当0≤x<2时,f(x)=x3-x,则函数y=f(x)的图象在区间[0,6]上与x轴的交点个数为____.
解析 因为当0≤x<2时,f(x)=x3-x.又f(x)是R上最小正周期为2的周期函数,且f(0)=0,则f(6)=f(4)=f(2)=f(0)=0.又f(1)=0,∴f(3)=f(5)=f(1)=0, 故函数y=f(x)的图象在区间[0,6]上与x轴的交点有7个.
16.已知函数f(x)=2|x-2|+ax(x∈R)有最小值.(1)求实数a的取值范围;
∴-2≤a≤2,故a的取值范围为[-2,2].
高中数学人教A版 (2019)必修 第一册第五章 三角函数5.4 三角函数的图象与性质集体备课课件ppt: 这是一份高中数学人教A版 (2019)必修 第一册第五章 三角函数5.4 三角函数的图象与性质集体备课课件ppt,共47页。PPT课件主要包含了目标认知,fx+T,周期函数,最小正周期,坐标原点,xkπk∈Z等内容,欢迎下载使用。
高中数学人教A版 (2019)必修 第一册5.4 三角函数的图象与性质集体备课课件ppt: 这是一份高中数学人教A版 (2019)必修 第一册5.4 三角函数的图象与性质集体备课课件ppt,共36页。PPT课件主要包含了周期函数,fx+T,奇函数,偶函数等内容,欢迎下载使用。
高中数学人教A版 (2019)必修 第一册5.4 三角函数的图象与性质备课课件ppt: 这是一份高中数学人教A版 (2019)必修 第一册5.4 三角函数的图象与性质备课课件ppt,共38页。PPT课件主要包含了内容索引,课前篇自主预习,课堂篇探究学习,课标阐释,思维脉络,知识点拨,最小正周期,答案0,答案A,答案C等内容,欢迎下载使用。














