沪科版九年级上册第22章 相似形22.1 比例线段精品课时作业

2021-2022学年九年级数学上册尖子生同步培优题典【沪科版】

            专题22.2比例线段（2）

姓名：__________________     班级：______________   得分：_________________

注意事项：

本试卷满分100分，试题共24题，选择10道、填空8道、解答6道．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．

一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．

1．（2021•醴陵市模拟）如图，直线l1∥l2∥l3，直线AC和DF被l1，l2，l3所截，如果AB＝2，BC＝3，EF＝2，那么DE的长是（　　）

A．2 B． C．1 D．

【分析】根据平行线分线段成比例定理得出比例式，代入求出即可．

【解析】∵直线l1∥l2∥l3，

∴，

∵AB＝2，BC＝3，EF＝2，

∴，

∴DE，

故选：B．

2．（2020秋•德保县期末）如图，已知D、E分别为AB、AC上的两点，且DE∥BC，AE＝3CE，AB＝8，则AD的长为（　　）

A．3 B．4 C．5 D．6

【分析】利用平行线分线段成比例定理得到，然后根据比例性质求出D．

【解析】∵DE∥BC，

∴，

∴AD8＝6．

故选：D．

3．（2020秋•莲湖区期末）如图，在△ABC中，DE∥AB，且，则的值为（　　）

A． B． C． D．

【分析】根据平行线分线段成比例定理列出比例式解答即可．

【解析】∵DE∥AB，

∴，

故选：D．

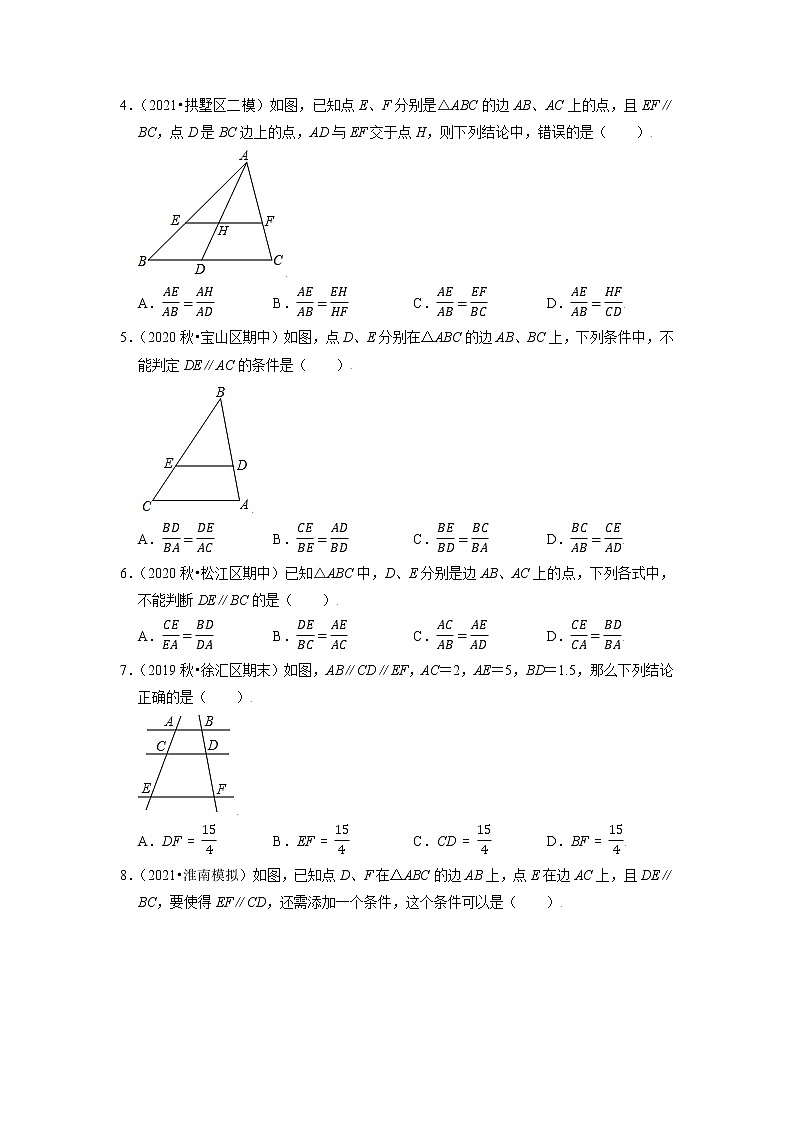
4．（2021•拱墅区二模）如图，已知点E、F分别是△ABC的边AB、AC上的点，且EF∥BC，点D是BC边上的点，AD与EF交于点H，则下列结论中，错误的是（　　）

A． B． C． D．

【分析】利用平行线分线段成比例定理即可一一判断．

【解析】∵EF∥BC，

∴，，，

∴选项A，C，D正确，

故选：B．

5．（2020秋•宝山区期中）如图，点D、E分别在△ABC的边AB、BC上，下列条件中，不能判定DE∥AC的条件是（　　）

A． B． C． D．

【分析】根据平行线分线段成比例定理对各个选项进行判断即可．

【解析】A、∵，不能判定DE∥AC，选项符合题意；

B、∵，∴DE∥AC，选项不符合题意；

C、∵，∴，∴DE∥AC，选项不符合题意；

D、∵，∴，∴DE∥AC，选项不符合题意；

故选：A．

6．（2020秋•松江区期中）已知△ABC中，D、E分别是边AB、AC上的点，下列各式中，不能判断DE∥BC的是（　　）

A． B． C． D．

【分析】若使DE∥BC，则其对应边必成比例，进而依据对应边成比例即可判定DE∥BC．

【解析】如图，若使线段DE∥BC，则其对应边必成比例，

即，，，

故B选项答案错误；

故选：B．

7．（2019秋•徐汇区期末）如图，AB∥CD∥EF，AC＝2，AE＝5，BD＝1.5，那么下列结论正确的是（　　）

A．DF B．EF C．CD D．BF

【分析】根据平行线分线段成比例定理判断即可．

【解析】∵AB∥CD∥EF，AC＝2，AE＝5，BD＝1.5，

∴，

即，

解得：DF，

∴BF＝BD+DF，

故选：D．

8．（2021•淮南模拟）如图，已知点D、F在△ABC的边AB上，点E在边AC上，且DE∥BC，要使得EF∥CD，还需添加一个条件，这个条件可以是（　　）

A． B． C． D．

【分析】由平行线分线段成比例可以得到，则根据等量代换可以推知，进而得出EF∥CD．

【解析】∵DE∥BC，

∴，

∴当时，，

∴EF∥CD，故C选项符合题意；

而A，B，D选项不能得出EF∥CD，

故选：C．

9．（2021•宜兴市模拟）如图，在△ABC中，D是BC上一点，连接AD，，F是AD的中点，连接BF并延长交AC于E，则的值是（　　）

A． B． C． D．

【分析】过D点作DH∥BE交AC于H，如图，根据平行线分线段成比例定理，先利用FE∥DH得到1，即AE＝EH，再由DH∥BE，，则CE＝4AE，从而得到的值．

【解析】过D点作DH∥BE交AC于H，如图，

∵F点为AD的中点，

∴AF＝FD，

∵FE∥DH，

∴1，即AE＝EH，

∵DH∥BE，

∴，CH＝3EH，

∴．

故选：A．

10．（2020秋•三明期末）如图，直线l1∥l2∥l3，直线AC分别交l1，l2，l3于点A，B，C，过点B的直线DE分别交l1，l3于点D，E．若AB＝2，BC＝4，BD＝3，则线段BE的长为（　　）

A．4 B．5 C．6 D．9

【分析】根据平行线分线段成比例定理，列出比例式求解即可得到答案．

【解析】∵l1∥l2∥l3，AB＝2，BC＝4，BD＝3，

∴，

∴，

解得：BE＝6，

故选：C．

二、填空题（本大题共8小题，每小题3分，共24分）请把答案直接填写在横线上

11．（2020•余杭区模拟）如图，直线l1∥l2∥l3，直线AF分别交l1，l2，l3于点A，D，F，直线BE分别交l1，l2，l3于点B，C，E，两直线AF，BE相交于点O．若AD＝DF，OA＝OD，则　　．

【分析】由平行线分线段成比例定理得出比例式，即可得出结果．

【解析】∵AD＝DF，OA＝OD，

∴，

∵l1∥l2∥l3，AD＝DF，OA＝OD，

∴，

故答案为．

12．（2020秋•宜宾期末）如图，AC∥EF∥BD，若AE：EB＝2：3，CD＝10，则CF＝　4　．

【分析】利用平行线分线段成比例定理得到，利用比例的性质得到，所以，从而可求出CF的长．

【解析】∵AC∥EF∥BD，

∴，

∵，

∴，

∴，

∴CF＝4．

故答案为4．

13．（2021•余杭区一模）如图，已知AC∥EF∥BD．如果AE：EB＝2：3，CF＝6．那么CD的长等于　15　．

【分析】根据平行线分线段成比例定理得到，这样可求出FD的长，然后计算CF+FD即可．

【解析】∵AC∥EF∥BD，

∴，

∴FDCF6＝9，

∴CD＝CF+FD＝6+9＝15．

故答案为15．

14．（2020秋•松江区期末）如图，已知直线l1、l2、l3分别交直线l4于点A、B、C，交直线l5于点D、E、F，且l1∥l2∥l3，AB＝4，AC＝6，DF＝10，则DE＝　　．

【分析】直接根据平行线分线段成比例定理得到，然后根据比例的性质可计算出DE的长．

【解析】∵l1∥l2∥l3，

∴，即，

∴DE．

故答案为．

15．（2021•深圳模拟）如图，△ABC中，D、F在AB边上，E、G在AC边上，DE∥FG∥BC，且AD：DF：FB＝3：2：1，若AG＝15，则EC的长为　9　．

【分析】根据平行线分线段成比例定理和已知条件得出AD：DF：FB＝AE：EG：GC＝3：2：1，设AE＝3x，EG＝2x，GC＝x，根据AG＝15得出方程3x+2x＝15，求出x，再求出答案即可．

【解析】∵DE∥FG∥BC，

∴AD：DF：FB＝AE：EG：GC，

∵AD：DF：FB＝3：2：1，

∴AE：EG：GC＝3：2：1，

设AE＝3x，EG＝2x，GC＝x，

∵AG＝15，

∴3x+2x＝15，

解得：x＝3，

即AE＝9，EG＝6，GC＝3，

∴EC＝EG+GC＝6+3＝9，

故答案为：9．

16．（2020春•静安区校级期末）如图，在梯形ABCD中，AD∥BC．点E、F、G在边AB上，点H、I、J在边CD上，且AE＝EF＝FG＝GB，DH＝HI＝IJ＝JC．如果AD＝2，GJ＝5，那么BC＝　6　．

【分析】过D点作DM∥AB交BC于M，交GJ于N，如图，易得四边形ADNG，四边形ADMB为平行四边形的性质，则GN＝BM＝AD＝2，再利用NJ∥MC，根据平行线分线段成比例定理得到，所以MC＝4，

从而得到BC的长．

【解析】过D点作DM∥AB交BC于M，交GJ于N，如图，

∵AE＝EF＝FG＝GB，DH＝HI＝IJ＝JC．

∴AE：EF：FG：GB＝DH：HI：IJ：JC，

∴GN∥AD∥BM，

∴四边形ADNG，四边形ADMB为平行四边形的性质，

∴GN＝BM＝AD＝2，

∴NJ＝3，

∵NJ∥MC，

∴，

∴MC＝4，

∴BC＝BM+MC＝2+4＝6．

故答案为6．

17．（2021•郴州）如图是一架梯子的示意图，其中AA1∥BB1∥CC1∥DD1，且AB＝BC＝CD．为使其更稳固，在A，D1间加绑一条安全绳（线段AD1）量得AE＝0.4m，则AD1＝　1.2　m．

【分析】根据平行线分线段成比例定理得到AE＝EF，同理得到AD1＝3AE，计算即可．

【解析】∵BB1∥CC1，

∴，

∵AB＝BC，

∴AE＝EF，

同理可得：AE＝EF＝FD1，

∵AE＝0.4m，

∴AD1＝0.4×3＝1.2（m），

故答案为：1.2．

18．（2021•铁岭模拟）如图，a∥b∥c，直线l1，l2与这三条平行线分别交于点A，B，C和点D，E，F．若AB＝6，BC＝9，DF＝12，则EF＝　7.2　．

【分析】根据平行线分线段成比例定理列出比例式，代入已知数据计算即可．

【解析】∵a∥b∥c，

∴，即，

解得，EF＝7.2，

故答案为：7.2．

三、解答题（本大题共6小题，共46分．解答时应写出文字说明、证明过程或演算步骤）

19．（2020秋•浦东新区期末）如图，已知AD∥BE∥CF，它们依次交直线l1、l2于点A、B、C和点D、E、F，且AB＝6，BC＝8．

（1）求的值；

（2）当AD＝5，CF＝19时，求BE的长．

【分析】（1）直接根据平行线分线段成比例定理求解；

（2）过D点作DM∥AC交CF于M，交BE于N，如图，易得四边形ABND和四边形ACMD都是平行四边形，所以BN＝CM＝AD＝5，则MF＝14，再利用NE∥MF，所以，然后利用比例的性质计算出NE，最后计算BN+NE即可．

【解析】（1）∵AD∥BE∥CF，

∴；

（2）过D点作DM∥AC交CF于M，交BE于N，如图，

∵AD∥BN∥CM，AC∥DM，

∴四边形ABND和四边形ACMD都是平行四边形，

∴BN＝AD＝5，CM＝AD＝5，

∴MF＝CF﹣CM＝19﹣5＝14，

∵NE∥MF，

∴，

∴NEMF14＝6，

∴BE＝BN+NE＝5+6＝11．

20．（2020春•文登区期中）如图，已知DE∥BC，FE∥CD，AF＝3，AD＝5，AE＝4．

（1）求CE的长；

（2）求AB的长．

【分析】根据平行线分线段成比例定理列出比例式，代入计算即可．

【解析】（1）∵FE∥CD，

∴，即，

解得，AC，

则CE＝AC﹣AE4；

（2）∵DE∥BC，

∴，即，

解得，AB．

21．（2019秋•黄浦区期中）如图，已知在△ABC中，EF∥CD，AF＝3，AD＝5，AE＝4．

（1）求CE的长；

（2）当AB时，求证：DE∥BC．

【分析】（1）根据平行线分线段成比例定理得出比例式，求出AC，再求出CE即可；

（2）根据已知线段的长度求出，根据相似三角形的判定得出△ADE∽△ABC，根据相似三角形的性质得出∠ADE＝∠B，根据平行线的判定得出即可．

【解析】（1）∵EF∥CD，

∴，

∵AF＝3，AD＝5，AE＝4，

∴，

解得：AC，

∵AE＝4，

∴CE＝AC﹣AE4；

（2）∵AB，AD＝5，AE＝4，AC，

∴，

∵∠A＝∠A，

∴△ADE∽△ABC，

∴∠ADE＝∠B，

∴DE∥BC．

22．如图，已知AD∥BE∥CF，如果AB＝3，AC＝7，EF＝6．

（1）求DE的长．

（2）如果AC与DF相交于点O，OF＝1，求．

【分析】（1）利用平行线分线段成比例定理得到，即，然后根据比例的性质求出DE的长；

（2）先计算出OE、OD，然后利用AD∥CF得到．

【解析】（1）∵AD∥BE∥CF，

∴，即，

∴DE；

（2）∵OF＝1，

∴OE＝6﹣1＝5，

∴OD＝5，

∵AD∥CF，

∴．

23．（2019秋•安徽月考）如图，l1∥l2∥l3，ABAC，DF＝9，求EF的长．

【分析】先求出，根据平行线分线段成比例定理得出比例式，代入求出即可．

【解析】∵ABAC，

∴，

∴，

∵l1∥l2∥l3，

∴，

∵DF＝9，

∴，

解得：EF．

24．（2020•浦东新区三模）如图，在Rt△ABC中，∠ACB＝90°，∠BAC＝60°，AC＝6，AD平分∠BAC，交边BC于点D，过点D作CA的平行线，交边AB于点E．

（1）求线段DE的长；

（2）取线段AD的中点M，联结BM，交线段DE于点F，延长线段BM交边AC于点G，求的值．

【分析】（1）根据平行线分线段成比例定理，列出比例式求解即可；

（2）根据平行线分线段成比例定理，列出比例式求解即可．

【解析】（1）∵AD平分∠BAC，∠BAC＝60°，

∴∠DAC＝30°，

在Rt△ACD中，∠ACD＝90°，∠DAC＝30°，AC＝6，

∴CD＝2，

在Rt△ACB中，∠ACB＝90°，∠BAC＝60°，AC＝6，

∴BC＝6，

∴BD＝BC﹣CD＝4，

∵DE∥CA，

∴，

∴DE＝4；

（2）如图，

∵点M是线段AD的中点，

∴DM＝AM，

∵DE∥CA，

∴，

∴DF＝AG，

∵DE∥CA，

∴，

∴，

∵BD＝4，BC＝6，DF＝AG，

∴．