高中数学人教A版 (2019)必修第一册3.2 函数的基本性质课堂教学ppt课件

展开

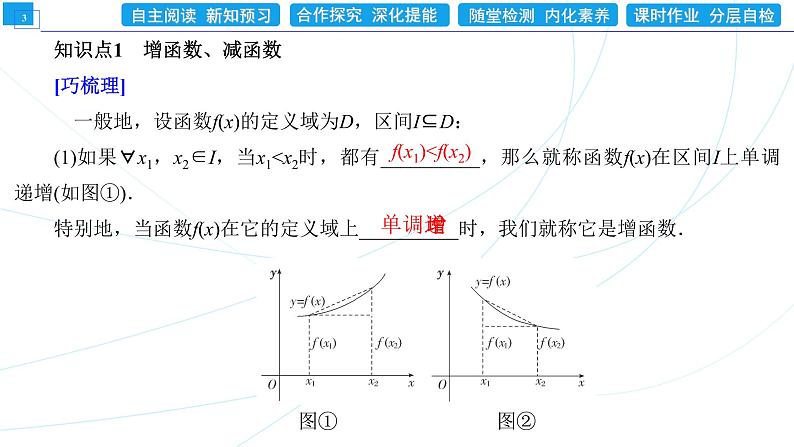
这是一份高中数学人教A版 (2019)必修第一册3.2 函数的基本性质课堂教学ppt课件，共49页。PPT课件主要包含了自主阅读·新知预习，合作探究·深化提能，随堂检测·内化素养，课时作业·分层自检等内容，欢迎下载使用。

知识点1　增函数、减函数[巧梳理]　一般地，设函数f(x)的定义域为D，区间I⊆D：(1)如果∀x1，x2∈I，当x1f(x1)(2)如果∀x1，x2∈I，当x1f(x1)>f(x2)
[微点拨]x1，x2的三个特征(1)同区间性，即x1，x2∈I；(2)任意性，即不可用区间I上的两个特殊值代替x1，x2；(3)有序性，即需要区分大小，通常规定x1知识点2　函数的单调性与单调区间[巧梳理]如果函数y＝f(x)在区间I上__________或__________，那么就说函数y＝f(x)在这一区间具有(严格的)单调性，区间I叫做y＝f(x)的__________．
3．函数f(x)＝x2＋2x＋1的单调递减区间是________．答案：(－∞，－1]
利用定义证明函数单调性的步骤(1)取值：设x1，x2是给定区间内的任意两个值，且x1学习任务二　由图象确定函数的单调区间[例2]　已知函数f(x)＝x2－4|x|＋3，x∈R.根据图象写出它的单调区间．
对于能作出图象的函数，都可应用图象法判断其单调性．图象法主要应用于常见函数(如一次函数、二次函数、反比例函数等)的单调性判断，或应用于能通过常见函数图象的平移、翻折等变换得到所给函数的图象的函数单调性的判断．
[跟踪训练]2．画出函数y＝|x|(x－2)的图象，并指出函数的单调区间．
学习任务三　函数单调性的应用角度1　比较大小或解不等式[例3]　若函数f(x)在区间(－∞，＋∞)上是减函数，则下列关系式一定成立的是(　　)A．f(a)>f(2a)　　　B．f(a2)a2，且函数y＝f(x)在R上是减函数，所以f(a2＋1)[例4]　已知函数y＝f(x)是(－∞，＋∞)上的增函数，且f(2x－3)>f(5x＋6)，则实数x的取值范围是________．解析：因为f(x)在(－∞，＋∞)上是增函数，且f(2x－3)>f(5x＋6)，所以2x－3>5x＋6，即x<－3，所以x的取值范围是(－∞，－3)．答案：(－∞，－3)
利用单调性比较大小或解不等式的方法(1)利用函数的单调性可以比较函数值或自变量的大小．在解决比较函数值的问题时，要注意将对应的自变量转化到同一个单调区间上．(2)在求解与抽象函数有关的不等式时，往往是利用函数的单调性将“f”符号脱掉，使其转化为具体的不等式求解．此时应特别注意函数的定义域．
角度2　求参数的取值范围[例5]　若函数f(x)＝－x2＋2(a－1)x＋2在(－∞，4)上是增函数，则实数a的取值范围是(　　)A．a≥5 B．a≥3C．a≤3 D．a≤－5解析：A　函数f(x)＝－x2＋2(a－1)x＋2的图象开口向下，对称轴为直线x＝a－1，故该函数的单调递增区间为(－∞，a－1)．又函数f(x)在(－∞，4)上是增函数．所以(－∞，4)⊆(－∞，a－1)，所以a－1≥4，a≥5.故选A.
已知函数的单调性求参数的取值范围的一般方法(1)将参数看成已知数，求函数的单调区间，再与已知的单调区间比较，求出参数的取值范围；(2)运用函数单调性的定义建立关于参数的不等式(组)，解不等式(组)求出参数的取值范围．
1.函数y＝f(x)，x∈[－4，4]的图象如图所示，则f(x)的单调递增区间是(　　)A．[－4，4]B．[－4，－3]∪[1，4]C．[－3，1]D．[－3，4]解析：C　由图象知单调递增区间为[－3，1]．
2．已知函数f(x)＝x2－2mx－3在区间[1，2]上单调，则实数m的取值范围为________．解析：∵函数f(x)＝x2－2mx－3的对称轴为x＝m，且f(x)在[1，2]上单调，∴m≥2或m≤1答案：(－∞，1]∪[2，＋∞)
3．已知f(x)是定义在R上的增函数，且f(x2－2)解析：C　因为f(x)在[a，b]上单调递增，对于任意的x1，x2∈[a，b](x1≠x2)，x1－x2与f(x1)－f(x2)的符号相同，故A，B，D都正确，而C中应为若x13．已知定义域为R的函数f(x)在(4，＋∞)上单调递减，且函数y＝f(x)的对称轴为x＝4，则(　　)A．f(2)>f(3) B．f(2)>f(5)C．f(3)>f(5) D．f(3)>f(6)解析：D　∵f(x)关于x＝4对称且在(4，＋∞)上单调递减，∴f(x)在(－∞，4)上单调递增，且f(5)＝f(3)，f(6)＝f(2)，∴f(3)>f(2)＝f(6)，故选D.
4．函数y＝|x＋2|在区间[－3，0]上(　　)A．递减 B．递增C．先减后增 D．先增后减
6．已知函数f(x)是R上的增函数，A(0，－1)，B(3，1)是其图象上的两点，则－1解析：当x≥1时，f(x)是增函数，当x<1时，f(x)是减函数，所以f(x)的单调递减区间为(－∞，1)．答案：(－∞，1)
8．已知函数y＝f(x)在定义域(－1，1)上是减函数，且f(1－a)13．设f(x)是定义在R上的增函数，f(xy)＝f(x)＋f(y)，f(3)＝1，则不等式f(x)＋f(－2)>1的解集为________．

相关课件更多