高中3.2 函数的基本性质第2课时学案及答案

这是一份高中3.2 函数的基本性质第2课时学案及答案，共15页。

1．理解函数的最大(小)值的概念及其几何意义．
2．会借助单调性求最值．
3．掌握求二次函数在闭区间上的最值．
1．最大值
(1)定义：一般地，设函数y＝f(x)的定义域为I，如果存在实数M满足：
①∀x∈I，都有f(x)≤M；
②∃x0∈I，使得f(x0)＝M.
那么，称M是函数y＝f(x)的最大值．
(2)几何意义：函数y＝f(x)的最大值是图象最高点的纵坐标．
2．最小值
(1)定义：一般地，设函数y＝f(x)的定义域为I，如果存在实数M满足：
①∀x∈I，都有f(x)≥M；
②∃x0∈I，使得f(x0)＝M.
那么，称M是函数y＝f(x)的最小值．
(2)几何意义：函数y＝f(x)的最小值是图象最低点的纵坐标．
温馨提示：(1)最大(小)值必须是一个函数值，是值域中的一个元素．
(2)并不是每一个函数都有最值，如函数y＝eq \f(1,x)，既没有最大值，也没有最小值．
(3)最值是函数的整体性质，即在函数的整个定义域内研究其最值．
1．函数y＝f(x)在[－2,2]上的图象如图所示，试指出此函数的最小值、最大值和相应的x的值．
[答案] f(x)的最小值为－1，此时x＝－2；
f(x)的最大值为2，此时x＝1
2．判断正误(正确的打“√”，错误的打“×”)
(1)任何函数都有最大值或最小值．( )
(2)函数的最小值一定比最大值小．( )
(3)函数f(x)＝－x在[2,3)上的最大值为－2，无最小值．( )
(4)函数最大值对应图象中的最高点，且该点只有一个．( )
[答案] (1)× (2)× (3)√ (4)×
题型一 图象法求函数的最大(小)值
【典例1】 (1)已知函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(x2，－1≤x≤1，,\f(1,x)，x>1.))求f(x)的最大值、最小值；
(2)画出函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(－\f(2,x)，x∈－∞，0，,x2＋2x－1，x∈[0，＋∞))的图象，并写出函数的单调区间，函数的最小值．
[思路导引] 作出函数f(x)的图象，结合图象求解．
[解] (1)作出函数f(x)的图象(如图1)．
由图象可知，当x＝±1时，f(x)取最大值为f(±1)＝1；当x＝0时，f(x)取最小值f(0)＝0，故f(x)的最大值为1，最小值为0.
(2)f(x)的图象如图2所示，f(x)的单调递增区间是(－∞，0)和[0，＋∞)，函数的最小值为f(0)＝－1.
图象法求最大(小)值的步骤
[针对训练]
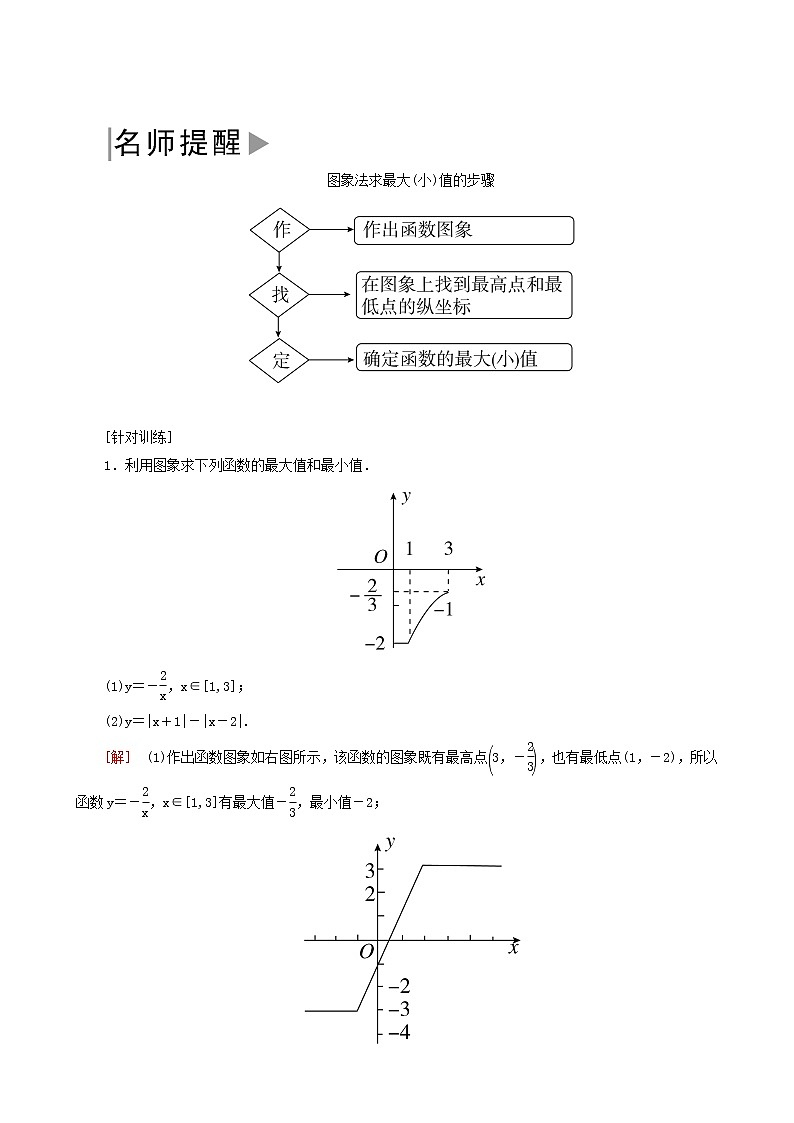
1．利用图象求下列函数的最大值和最小值．
(1)y＝－eq \f(2,x)，x∈[1,3]；
(2)y＝|x＋1|－|x－2|.
[解] (1)作出函数图象如右图所示，该函数的图象既有最高点eq \b\lc\(\rc\)(\a\vs4\al\c1(3，－\f(2,3)))，也有最低点(1，－2)，所以函数y＝－eq \f(2,x)，x∈[1,3]有最大值－eq \f(2,3)，最小值－2；
(2)y＝|x＋1|－|x－2|
＝eq \b\lc\{\rc\ (\a\vs4\al\c1(3，x≥2，,2x－1，－1作出函数的图象，由右图可知，y∈[－3,3]．所以函数的最大值为3，最小值为－3.
题型二 利用单调性求函数的最大(小)值
【典例2】 已知函数f(x)＝x＋eq \f(1,x).
(1)证明：f(x)在(1，＋∞)内是增函数；
(2)求f(x)在[2,4]上的最值．
[解] (1)证明：设∀x1，x2∈(1，＋∞)，且x1∵x2>x1>1，∴x1－x2<0，
又∵x1x2>1，∴x1x2－1>0，
故(x1－x2)·eq \f(x1x2－1,x1x2)<0，即f(x1)所以f(x)在(1，＋∞)内是增函数．
(2)由(1)可知f(x)在[2,4]上是增函数，
∴当x∈[2,4]时，f(2)≤f(x)≤f(4)．
又f(2)＝2＋eq \f(1,2)＝eq \f(5,2)，f(4)＝4＋eq \f(1,4)＝eq \f(17,4)，
∴f(x)在[2,4]上的最大值为eq \f(17,4)，最小值为eq \f(5,2).
函数的最值与单调性的关系
(1)如果函数y＝f(x)在区间(a，b]上是增函数，在区间[b，c)上是减函数，则函数y＝f(x)，x∈(a，c)在x＝b处有最大值f(b)．
(2)如果函数y＝f(x)在区间(a，b]上是减函数，在区间[b，c)上是增函数，则函数y＝f(x)，x∈(a，c)在x＝b处有最小值f(b)．
(3)如果函数y＝f(x)在区间[a，b]上是增(减)函数，则在区间[a，b]的左、右端点处分别取得最小(大)值、最大(小)值．
[针对训练]
2．已知函数f(x)＝eq \f(x,x－1)，x∈[2,5]，判断函数f(x)的单调性，并求函数f(x)的最大值和最小值．
[解] 任取2≤x1则f(x1)＝eq \f(x1,x1－1)，f(x2)＝eq \f(x2,x2－1)，
f(x2)－f(x1)＝eq \f(x2,x2－1)－eq \f(x1,x1－1)＝eq \f(x1－x2,x2－1x1－1)，
∵2≤x10，x1－1>0，
∴f(x2)－f(x1)<0.∴f(x2)∴f(x)＝eq \f(x,x－1)在区间[2,5]上是单调减函数．
f(x)max＝f(2)＝eq \f(2,2－1)＝2，
f(x)min＝f(5)＝eq \f(5,5－1)＝eq \f(5,4).
题型三 求二次函数的最大(小)值
【典例3】 (1)已知函数f(x)＝3x2－12x＋5，x∈[0,3]，求函数的最大值和最小值．
(2)求二次函数f(x)＝x2－2ax＋2在[2,4]上的最小值．
[思路导引] 找出f(x)的对称轴，分析对称轴与给定区间的关系，结合单调性求最值．
[解] (1)函数f(x)＝3x2－12x＋5＝3(x－2)2－7，函数f(x)＝3(x－2)2－7的图象如图所示，由图可知，函数f(x)在[0,2)上递减，在[2,3]上递增，并且f(0)＝5，f(2)＝－7，f(3)＝－4，所以在[0,3]上，f(x)max＝f(0)＝5，f(x)min＝f(2)＝－7.
(2)∵函数图象的对称轴是x＝a，
∴当a<2时，f(x)在[2,4]上是增函数，
∴f(x)min＝f(2)＝6－4a.
当a>4时，f(x)在[2,4]上是减函数，
∴f(x)min＝f(4)＝18－8a.
当2≤a≤4时，f(x)min＝f(a)＝2－a2.
∴f(x)min＝eq \b\lc\{\rc\ (\a\vs4\al\c1(6－4a，a<2，,2－a2，2≤a≤4，,18－8a，a>4.))
[变式] 本例(2)条件变为，若f(x)＝x2－2ax＋2，当x∈[2,4]时，f(x)≤a恒成立，求实数a的取值范围．
[解] 在[2,4]内，f(x)≤a恒成立，
即a≥x2－2ax＋2在[2,4]内恒成立，
即a≥f(x)max，x∈[2,4]．
又f(x)max＝eq \b\lc\{\rc\ (\a\vs4\al\c1(18－8a，a≤3，,6－4a，a>3.))
①当a≤3时，a≥18－8a，解得a≥2，此时有2≤a≤3.
②当a>3时，a≥6－4a，解得a≥eq \f(6,5)，此时有a>3.
综上有实数a的取值范围是[2，＋∞)．
求解二次函数最值问题的顺序
(1)确定对称轴与抛物线的开口方向、作图．
(2)在图象上标出定义域的位置．
(3)观察单调性写出最值．
[针对训练]
3．已知函数f(x)＝x2＋2x＋a(x∈[0,2])有最小值－2，则f(x)的最大值为( )
A．4 B．6 C．1 D．2
[解析] 函数f(x)＝x2＋2x＋a的对称轴为x＝－1，在[0,2]上为增函数，所以f(x)的最小值为f(0)＝a＝－2，f(x)的最大值为f(2)＝8＋a＝6.
[答案] B
4．已知函数f(x)＝x2－6x＋8，x∈[1，a]，并且f(x)的最小值为f(a)，则实数a的取值范围是________．
[解析] 如图可知f(x)在[1，a]内是单调递减的，
又∵f(x)的单调递减区间为(－∞，3]，∴1[答案] (1,3]
题型四 实际应用中的最值
【典例4】 某公司生产一种电子仪器的固定成本为20000元，每生产一台仪器需增加投入100元，已知总收益满足函数：R(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(400x－\f(1,2)x2，0≤x≤400，,80000，x>400.))
其中x是仪器的月产量．
(1)将利润表示为关于月产量的函数f(x)；
(2)当月产量为何值时，公司所获利润最大？最大利润为多少元？(总收益＝总成本＋利润)
[思路导引] 先将利润表示成关于x的函数，再利用函数的单调性求最值．
[解] (1)月产量为x台，则总成本为(20000＋100x)元，
从而f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(－\f(1,2)x2＋300x－20000，0≤x≤400，,60000－100x，x>400.))
(2)当0≤x≤400时，f(x)＝－eq \f(1,2)(x－300)2＋25000，
当x＝300时，f(x)max＝25000；
当x>400时，f(x)＝60000－100x是减函数，f(x)<60000－100×400＝20000<25000.
∴当x＝300时，f(x)max＝25000.
即每月生产300台仪器时公司所获利润最大，最大利润为25000元．
求解函数最大(小)值的实际问题应注意的2点
(1)解实际应用题要弄清题意，从实际出发，引入数学符号，建立数学模型，列出函数关系式，分析函数的性质，从而解决问题，要注意自变量的取值范围．
(2)实际应用问题中，最大利润、用料最省等问题常转化为求函数最值来解决．
[针对训练]
5．将进货单价为40元的商品按50元一个出售时，能卖出500个．已知这种商品每涨价1元，其销售量就减少10个，为得到最大利润，售价应为多少元？最大利润是多少？
[解] 设售价为x元，利润为y元，单个涨价(x－50)元，销量减少10(x－50)个．
∴y＝(x－40)(1000－10x)
＝－10(x－70)2＋9000≤9000.
故当x＝70时，ymax＝9000.
答：售价为70元时，利润最大为9000元.
课堂归纳小结
1．求函数最大(小)值的常用方法
(1)值域．求出函数f(x)的值域，即可求其最值(注意必须确保存在函数值里的最值)；
(2)单调性法．通过研究函数的单调性来求函数的最值；
(3)特殊函数法．利用特殊函数[如一次函数、二次函数、反比例函数、函数y＝x＋eq \f(a,x)(a>0)]的单调性来求其最值.
2.函数的值域与最大(小)值的区别
(1)函数的值域是一个集合，函数的最值是一个函数值，它是值域的一个元素，即定义域中一定存在一个x0，使f(x0)＝M(最值)．
(2)函数的值域一定存在，但函数并不一定有最大(小)值，如y＝x在x∈(－1,1)时无最值.
1．函数f(x)在[－2，＋∞)上的图象如图所示，则此函数的最大、最小值分别为( )
A．3,0
B．3,1
C．3，无最小值
D．3，－2
[解析] 观察图象可以知道，图象的最高点坐标是(0,3)，从而其最大值是3；另外从图象看，无最低点，即该函数不存在最小值．故选C.
[答案] C
2．已知函数f(x)＝|x|，x∈[－1,3]，则f(x)的最大值为( )
A．0 B．1 C．2 D．3
[解析] 作出函数f(x)＝|x|，x∈[－1,3]的图象，如图所示．根据函数图象可知，f(x)的最大值为3.
[答案] D
3．下列函数在[1,4]上最大值为3的是( )
A．y＝eq \f(1,x)＋2 B．y＝3x－2
C．y＝x2 D．y＝1－x
[解析] B、C在[1,4]上均为增函数，A、D在[1,4]上均为减函数，代入端点值，即可求得最值，故选A.
[答案] A
4.在如图所示的锐角三角形空地中，欲建一个面积最大的内接矩形花园(阴影部分)，则其边长x为________(m)．
[解析] 设矩形花园的宽为y m，
则eq \f(x,40)＝eq \f(40－y,40)，
即y＝40－x，矩形花园的面积S＝x(40－x)＝－x2＋40x＝－(x－20)2＋400，当x＝20时，面积最大．
[答案] 20
5．已知二次函数y＝x2－4x＋5，分别求下列条件下函数的最小值：
(1)x∈[－1,0]；(2)x∈[a，a＋1]．
[解] (1)∵二次函数y＝x2－4x＋5的对称轴为x＝2且开口向上，
∴二次函数在x∈[－1,0]上是单调递减的．
∴ymin＝02－4×0＋5＝5.
(2)当a≥2时，函数在x∈[a，a＋1]上是单调递增的，
ymin＝a2－4a＋5；
当a＋1≤2即a≤1时，函数在[a，a＋1]上是单调递减的，
ymin＝(a＋1)2－4(a＋1)＋5＝a2－2a＋2；
当a<2故函数的最小值为eq \b\lc\{\rc\ (\a\vs4\al\c1(a2－2a＋2，a≤1，,1，1课后作业(二十)
复习巩固
一、选择题
1．函数y＝f(x)(－2≤x≤2)的图象如右图所示，则函数的最大值、最小值分别为( )
A．f(2)，f(－2)
B．feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))，f(－1)
C．feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))，feq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(3,2)))
D．feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))，f(0)
[解析] 根据函数最值定义，结合函数图象可知，当x＝－eq \f(3,2)时，有最小值feq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(3,2)))；当x＝eq \f(1,2)时，有最大值feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2))).
[答案] C
2．函数y＝x2－2x＋2在区间[－2,3]上的最大值、最小值分别是( )
A．10,5 B．10,1
C．5,1 D．以上都不对
[解析] 因为y＝x2－2x＋2＝(x－1)2＋1，且x∈[－2,3]，所以当x＝1时，ymin＝1，当x＝－2时，ymax＝(－2－1)2＋1＝10.故选B.
[答案] B
3．函数y＝eq \f(3,x＋2)(x≠－2)在区间[0,5]上的最大值、最小值分别是( )
A.eq \f(3,7)，0 B.eq \f(3,2)，0
C.eq \f(3,2)，eq \f(3,7) D．最小值为－eq \f(1,4)，无最大值
[解析] 因为函数y＝eq \f(3,x＋2)在区间[0,5]上单调递减，所以当x＝0时，ymax＝eq \f(3,2)，当x＝5时，ymin＝eq \f(3,7).故选C.
[答案] C
4．若函数y＝ax＋1在[1,2]上的最大值与最小值的差为2，则实数a的值是( )
A．2B．－2
C．2或－2D．0
[解析] 由题意知a≠0，当a>0时，有(2a＋1)－(a＋1)＝2，解得a＝2；当a<0时，有(a＋1)－(2a＋1)＝2，解得a＝－2.综上知a＝±2.
[答案] C
5．当0≤x≤2时，a<－x2＋2x恒成立，则实数a的取值范围是( )
A．(－∞，1] B．(－∞，0]
C．(－∞，0) D．(0，＋∞)
[解析] 令f(x)＝－x2＋2x，
则f(x)＝－x2＋2x＝－(x－1)2＋1.
又∵x∈[0,2]，∴f(x)min＝f(0)＝f(2)＝0.
∴a<0.
[答案] C
二、填空题
6．函数y＝－eq \f(1,x)，x∈[－3，－1]的最大值与最小值的差是________．
[解析] 因为函数y＝－eq \f(1,x)在[－3，－1]上为增函数，所以ymin＝eq \f(1,3)，ymax＝1，
所以ymax－ymin＝1－eq \f(1,3)＝eq \f(2,3).
[答案] eq \f(2,3)
7．已知函数f(x)＝－x2＋4x＋a，x∈[0,1]，若f(x)有最小值－2，则f(x)的最大值为________．
[解析] 函数f(x)＝－x2＋4x＋a＝－(x－2)2＋4＋a，x∈[0,1]，且函数有最小值－2.
故当x＝0时，函数有最小值，
当x＝1时，函数有最大值．
∵当x＝0时，f(0)＝a＝－2，∴f(x)＝－x2＋4x－2，
∴当x＝1时，f(x)max＝f(1)＝－12＋4×1－2＝1.
[答案] 1
8.如图，某地要修建一个圆形的喷水池，水流在各个方向上以相同的抛物线路径落下，以水池的中央为坐标原点，水平方向为x轴、竖直方向为y轴建立平面直角坐标系．那么水流喷出的高度h(单位：m)与水平距离x(单位：m)之间的函数关系式为h(x)＝－x2＋2x＋eq \f(5,4)，x∈eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(5,2)))，则水流喷出的高度h的最大值是________m.
[解析] 由函数h(x)＝－x2＋2x＋eq \f(5,4)，x∈eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(5,2)))的图象可知，函数图象的顶点就是水流喷出的最高点．此时函数取得最大值．
对于函数h(x)＝－x2＋2x＋eq \f(5,4)，x∈eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(5,2)))，
若x＝1，函数有最大值h(x)max＝－12＋2×1＋eq \f(5,4)＝eq \f(9,4)(m)．
于是水流喷出的最高高度是eq \f(9,4)m.
[答案] eq \f(9,4)
三、解答题
9．已知函数f(x)＝eq \f(3,2x－1).
(1)证明：函数f(x)在eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)，＋∞))上是减函数；
(2)求函数f(x)在[1,5]上的最大值和最小值．
[解] (1)证明：设x1、x2是区间eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)，＋∞))上的任意两个实数，且x2>x1>eq \f(1,2)，
则f(x1)－f(x2)＝eq \f(3,2x1－1)－eq \f(3,2x2－1)
＝eq \f(6x2－x1,2x1－12x2－1).
由于x2>x1>eq \f(1,2)，
所以x2－x1>0，且(2x1－1)·(2x2－1)>0，
所以f(x1)－f(x2)>0，即f(x1)>f(x2)，
所以函数f(x)＝eq \f(3,2x－1)在区间eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)，＋∞))上是减函数．
(2)由(1)知，函数f(x)在[1,5]上是减函数，
因此，函数f(x)＝eq \f(3,2x－1)在区间[1,5]的两个端点上分别取得最大值与最小值，即最大值为f(1)＝3，最小值为f(5)＝eq \f(1,3).
10．求函数f(x)＝x2－2ax＋2在[－1,1]上的最小值．
[解] 函数f(x)图象的对称轴为直线x＝a，且函数图象开口向上，如图所示：
①当a>1时，f(x)在[－1,1]上单调递减，
故f(x)min＝f(1)＝3－2a；
②当－1≤a≤1时，f(x)在[－1,1]上先减后增，
故f(x)min＝f(a)＝2－a2；
③当a<－1时，f(x)在[－1,1]上单调递增，
故f(x)min＝f(－1)＝3＋2a.
综上可知f(x)的最小值为
f(x)min＝eq \b\lc\{\rc\ (\a\vs4\al\c1(3－2a，a>1，,2－a2，－1≤a≤1，,3＋2a，a<－1.))
综合运用
11．函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(2x＋6，x∈[1，2]，,x＋7，x∈[－1，1]，))则f(x)的最大值与最小值分别为( )
A．10,6 B．10,8
C．8,6 D．以上都不对
[解析] ∵x∈[1,2]时，f(x)max＝2×2＋6＝10，f(x)min＝2×1＋6＝8；x∈[－1,1]时，f(x)max＝1＋7＝8，f(x)min＝－1＋7＝6，∴f(x)max＝10，f(x)min＝6.
[答案] A
12．已知函数y＝x2－2x＋3在闭区间[0，m]上有最大值3，最小值2，则m的取值范围是( )
A．[1，＋∞) B．[0,2]
C．(－∞，2] D．[1,2]
[解析] f(x)＝(x－1)2＋2，∵f(x)min＝2，f(x)max＝3，且f(1)＝2，f(0)＝f(2)＝3，∴1≤m≤2，故选D.
[答案] D
13．某公司在甲、乙两地同时销售一种品牌车，销售x辆该品牌车的利润(单位：万元)分别为L1＝－x2＋21x和L2＝2x.若该公司在两地共销售15辆，则能获得的最大利润为( )
A．90万元B．60万元
C．120万元D．120.25万元
[解析] 设公司在甲地销售x辆，则在乙地销售(15－x)辆，公司获利为L＝－x2＋21x＋2(15－x)
＝－x2＋19x＋30＝－eq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(19,2)))2＋30＋eq \f(192,4)，
∴当x＝9或10时，L最大为120万元．
[答案] C
14．函数y＝|x＋1|＋|x－2|的最小值为________．
[解析] 化简函数为
y＝eq \b\lc\{\rc\ (\a\vs4\al\c1(－2x＋1，x≤－1，,3，－12，))
其图象如图所示，
所以函数的最小值为3.
[答案] 3
15．已知函数f(x)对任意x，y∈R，总有f(x)＋f(y)＝f(x＋y)，且当x>0时，f(x)<0，f(1)＝－eq \f(2,3).
(1)求证：f(x)是R上的单调减函数．
(2)求f(x)在[－3,3]上的最小值．
[解] (1)证明：设x1，x2是任意的两个实数，且x1则x2－x1>0，因为x>0时，f(x)<0，
所以f(x2－x1)<0，
又因为x2＝(x2－x1)＋x1，
所以f(x2)＝f[(x2－x1)＋x1]
＝f(x2－x1)＋f(x1)，
所以f(x2)－f(x1)＝f(x2－x1)<0，
所以f(x2)所以f(x)是R上的单调减函数．
(2)由(1)可知f(x)在R上是减函数，
所以f(x)在[－3,3]上也是减函数，
所以f(x)在[－3,3]上的最小值为f(3)．
而f(3)＝f(1)＋f(2)＝3f(1)＝3×eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(2,3)))＝－2.
所以函数f(x)在[－3,3]上的最小值是－2.