初中21.3 实际问题与一元二次方程课文配套课件ppt

这是一份初中21.3 实际问题与一元二次方程课文配套课件ppt，共24页。PPT课件主要包含了问题引入，探究归纳，下降率，下降前的量，×100%，解方程得，整理方程得，合作探究，1+x，变式训练等内容，欢迎下载使用。

小明学习非常认真，学习成绩直线上升，第一次月考数学成绩是 75 分，第二次月考增长了 20%，第三次月考又增长了 20%，问他第三次数学成绩是多少？
第二次数学成绩：75×(1 + 20%) = 90 (分)；
第三次数学成绩：90×(1 + 20%) = 108 (分).
即第三次数学成绩：75×(1 + 20%)2 = 108 (分).
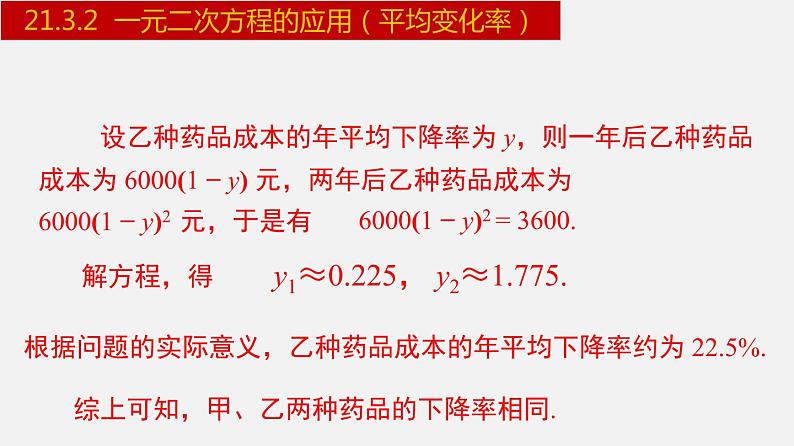
21.3.2 一元二次方程的应用（平均变化率）
两年前生产 1 t 甲种药品的成本是 5000 元，生产 1 t 乙种药品的成本是 6000 元. 随着生产技术的进步，现在生产 1 t 甲种药品的成本是 3000 元，生产 1 t 乙种药品的成本是 3600 元. 哪种药品成本的年平均下降率较大？
下降前的量−下降后的量
类型一：平均变化率与一元二次方程
分析：容易求出，甲种药品成本的年平均下降额为(5000 − 3000)÷2=1000(元)，乙种药品成本的年平均下降额为(6000 − 3600)÷2=1200(元)，显然，乙种药品成本的年平均下降额较大.但是，年平均下降额 (元) 不等同于年平均下降率 (百分数).
解：设甲种药品成本的年平均下降率为 x，则一年后甲种药品成本为 5000(1 − x) 元，两年后甲种药品成本为 5000(1 − x)2 元，于是有
5000(1 − x)2 = 3000.
x1≈0.225，x2≈1.775.
根据问题的实际意义，甲种药品成本的年平均下降率约为 22.5%.
一般下降率不可为负，且不大于 1.
设乙种药品成本的年平均下降率为 y，则一年后乙种药品成本为 6000(1 − y) 元，两年后乙种药品成本为6000(1 − y)2 元，于是有
6000(1 − y)2 = 3600.
y1≈0.225， y2≈1.775.
根据问题的实际意义，乙种药品成本的年平均下降率约为 22.5%.
综上可知，甲、乙两种药品的下降率相同.
例1 某药品经两次降价，零售价降为原来的一半. 已知两次降价的百分率一样，求每次降价的百分率（精确到 0.1%）.
解：设原价为 1 个单位，每次降价的百分率为 x.根据题意，得
答：每次降价的百分率约为 29.3%.
例2 为做好延迟开学期间学生的在线学习服务工作，某城市教育局推出“中小学延迟开学期间网络课堂”，为学生提供线上学习，据统计，第一批公益课受益学生 20万人次，第三批公益课受益学生 24.2 万人次．如果第二批，第三批公益课受益学生人次的增长率相同，求这个增长率.
解：设增长率为 x，根据题意，得 20(1 + x)2 = 24.2.解得 x1 = −2.1 (舍去)，x2 = 0.1 = 10%．答：增长率为 10%.
增长率不可为负，但可以超过 1.
问题 你能总结出有关增长率和降低率问题的数量关系式吗？
若平均增长(或降低)百分率为 x，增长(或降低)前的量是 a，增长(或降低) n 次后的量是 b，则它们的数量关系可表示为a(1±x)n = b (其中增长取“+”，降低取“-”).
例3 某公司去年的各项经营中，一月份的营业额为 200万元，一月、二月、三月的营业额共 950 万元，如果平均每月营业额的增长率相同，求这个增长率．
解：设这个增长率为 x. 根据题意，得
答：这个增长率为 50%.
200 + 200(1 + x) + 200(1 + x)2 = 950，
4x2 + 12x - 7 = 0.
x1 = −3.5 (舍去)，x2 = 0.5 = 50%.
填空：假设某种商品每件的成本为 2 元，售价为 3 元时，可卖 100 件.
(1) 此时的利润 w = 元；
(2) 若售价涨了 1 元，每件利润为_____元，同时少卖了 10 件，销售量为_____件，利润 w =_____元；
(3) 若售价涨了 2 元，每件利润为_____元，同时少卖了 20 件，销售量为____件，利润 w =_____元；
类型二：销售问题与一元二次方程
(4) 若售价涨了 3 元，每件利润为____元，同时少卖了 30 件，销售量为____件，利润 w =______元；
(5) 若售价涨了 x 元，每件利润为________元，同时少卖了____件，销售量为___________件，利润 w =________________ 元.
(100 − 10x)
(1 + x)(100 − 10 x)
想一想 若想售卖这种商品获取利润 300 元，则每件商品应涨价多少元？
解：设单价涨了 x 元，
依题意得 (1 + x)(100 - 10x) = 300，
解得 x1 = 4，x2 = 5.
即当每件商品涨价 4 元或 5 元时，能获得 300 元利润.
即 x2 − 9x + 20 = 0.
假设某种糖的成本为每千克 8 元，售价为 12 元时，可卖 100 千克. 若售价涨了 1 元，则少卖了 5 千克，要想售卖这种糖果获取利润 640 元，且售价不高于成本价的 2.5 倍，则每千克糖应涨价多少元？
解：设售价涨了 x 元，
依题意得 (4 + x)(100 − 5x) = 640，
解得 x1 = 4，x2 = 12.
∵ 售价不高于成本价的 2.5 倍，即
x + 12≤2.5×8，
答：每千克糖应涨价 4 元.
即 x2 − 16x + 48 = 0.
解：设每件衬衫降价 x 元，根据题意得 (40 − x)(20 + 2x) = 1200， 整理得 x2 − 30x + 200 = 0. 解方程得 x1 = 10，x2 = 20. 答：每件衬衫应降价 10 元或 20 元.
例4 某商场销售一批衬衫，平均每天可售出 20 件，每件盈利 40 元．经调查发现，如果每件衬衫降价 1 元，商场平均每天可多售出 2 件．若商场平均每天要盈利1200 元，每件衬衫应降价多少元？
增加条件：为了扩大销售，增加盈利，尽快减少库存，商场决定采取适当的降价措施. 若商场平均每天要盈利1200 元，每件衬衫应降价多少元？
解：设每件衬衫降价 x 元，根据题意得 (40 − x)(20 + 2x) = 1200， 整理得，x2 − 30x + 200 = 0. 解方程得，x1 = 10，x2 = 20. 因为要尽快减少库存，所以应取 x = 20. 答：每件衬衫应降价 20 元.
总结：列一元二次方程解“每每问题”的五个步骤．①设每件商品涨价（降价）x元（有时设新的定价为未知数）；②用含x的代数式表示每件商品的利润P；③用含x的代数式表示涨价（降价）后商品的销售量Q；④根据“每件商品的利润×销售量=销售利润”，得P·Q＝总利润；⑤解方程，取舍，作答．
注意：涨价时，销售量要保证大于0；降价时，要保证单个利润大于0
列一元二次方程解决利润问题的“一二三”1.一个相等关系:单件利润×销售数量=总利润.2.两个变量:单件利润、销售数量是较难表示的两个量.3.三个检验:列方程后检验每项意义、检验方程根求解 是否正确、作答前验根是否符合实际.
1. 某厂今年一月份的总产量为 500 吨，三月份的总产量为 720 吨，平均每月的增长率是 x，则可列方程( ) A. 500(1 + 2x) = 720 B. 500(1 + x)2 = 720 C. 500(1 + x2) = 720 D. 720(1 + x)2 = 500 2. 某校去年对实验器材的投资为 2 万元，预计今、明两年的投资总额为 8 万元．若设该校今、明两年在实验器材投资上的年平均增长率是 x，则可列方程为 .
2(1 + x) + 2(1 + x)2 = 8
3. 某村种的水稻前年平均每公顷产 7200 千克，今年平均每公顷产 8712 千克，求该村这两年水稻每公顷产量的年平均增长率.
解：设水稻每公顷产量的年平均增长率为 x. 根据题意，得 7200(1 + x)2 = 8712， 整理得 (1 + x)2 = 1.21. 解得 x1 = -2.1 (不符合题意，舍去)，x2 = 0.1 = 10%.答：水稻每公顷产量的年平均增长率为 10%.
4. 某超市将进货单价为 40 元的商品按 50 元出售时，能卖 500 个，已知该商品要涨价 1 元，其销售量就要减少 10 个，为了赚 8000 元利润，售价应定为多少，这时应进货多少个？
根据每件商品的利润×件数 = 总利润，
分析：设每件商品涨价 x 元，则商品售价为_______元，
则每个商品的利润为______________元，
因为每涨价 1 元，其销售会减少 10 个，则每个涨价 x 元，其销售量会减少____个，故销售量为__________个，
可列方程为______________________________.
[(50 + x) − 40]
(500 − 10x)
(500 − 10x)·[(50 + x) − 40] = 8000
解：设每个商品涨价 x 元，则单件利润为(50 + x - 40)元，销售量为 (500 − 10x) 个，则 (500 − 10x) · (50 + x − 40) = 8000，整理得 x2 − 40x + 300 = 0. 解得 x1 = 10，x2 = 30，都符合题意.当 x = 10 时，50 + x = 60，500 - 10x = 400；当 x = 30 时，50 + x = 80， 500 - 10x = 200.答：要想赚 8000 元，售价应定为 60 元/个，进货 400 个；或售价定为 80 元/个，进货 200 个.
5. 菜农小李种植的某蔬菜，计划以每千克 5 元的价格对外批发销售.由于部分菜农盲目扩大种植，造成该蔬菜滞销，小李为了加快销售，减少损失，对价格经过两次下调后，以每千克 3.2 元的价格对外批发销售.(1) 求平均每次下调的百分率；
解：设平均每次下调的百分率为 x， 由题意，得 5(1 − x)2 = 3.2. 解得 x1 = 1.8 (舍去)，x2 = 0.2 = 20%. ∴ 平均每次下调的百分率为 20%.
(2) 小华准备到小李处购买 5 吨该蔬菜，因数量多，小李决定再给予两种优惠方案以供选择：方案一，打九折销售；方案二，不打折，每吨优惠现金 200 元.试问小华选择哪种方案更优惠？请说明理由.
解：小华选择方案一购买更优惠，理由如下：方案一所需费用为：3.2×0.9×5000 = 14400(元)，方案二所需费用为：3.2×5000 − 200×5 = 15000(元)，∵ 14400＜15000，∴ 小华选择方案一购买更优惠.