人教版九年级上册21.3 实际问题与一元二次方程教学演示ppt课件

这是一份人教版九年级上册21.3 实际问题与一元二次方程教学演示ppt课件，共16页。PPT课件主要包含了解应用题的一般步骤，第二步列出方程，动手折一折，问题1，如何设未知数，x-10cm，整理得，x2-15x0，解这个方程得，∴x15等内容，欢迎下载使用。

第一步：设未知数(单位名称);
第三步：解这个方程，求出未知数的值；
第四步：查(1)值是否符合实际意义, (2)值是否使所列方程左右相等;
第五步：答题完整（单位名称）。
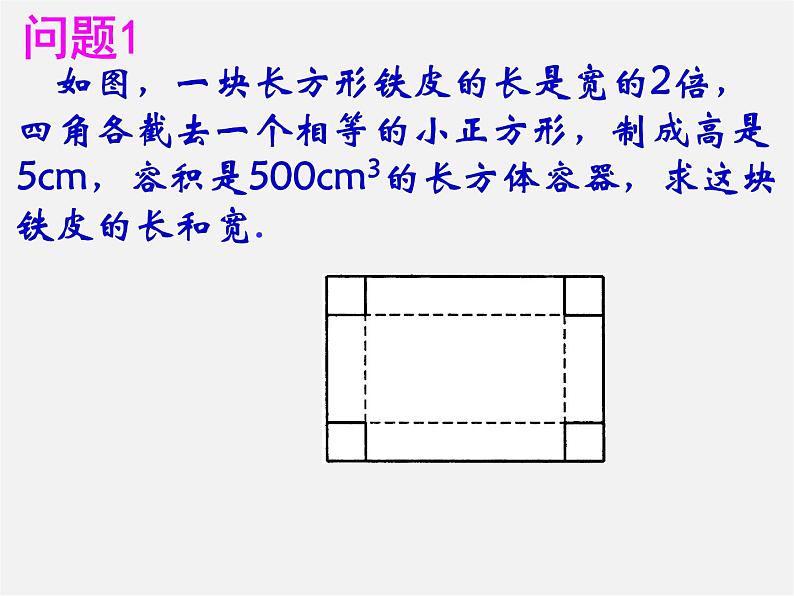
（1） 如何把一张长方形硬纸片折成 一个无盖的长方体纸盒？
（2） 无盖长方体的高与裁去的四个 小正方形的边长有什么关系？
　如图，一块长方形铁皮的长是宽的2倍，四角各截去一个相等的小正方形，制成高是5cm，容积是500cm3的长方体容器，求这块铁皮的长和宽.
如果设这块铁皮的宽是xcm，
那么制成的长方体容器底面的宽是_________
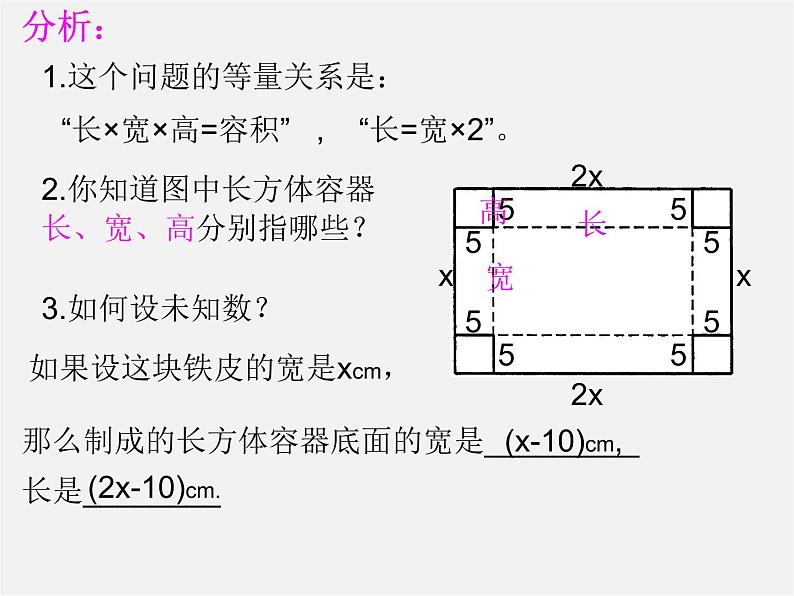
1.这个问题的等量关系是：
“长×宽×高=容积” , “长=宽×2”。
2.你知道图中长方体容器长、宽、高分别指哪些？
设这块铁皮的宽是xcm，那么制成的长方体容器底面的宽是(x-10)cm,长是(2x-10)cm.根据题意得:
5(x-10)(2x-10)=500
x1=15 x2=0
(不合题意,舍去)
答:这块铁皮的宽是15cm，长是30cm.
1.一块长方形菜地的面积是150m2,如果它的长减少5m,那么菜地就变成正方形.求原菜地的长和宽.
如果设原菜地宽为xm
x(x+5)=150
2.如图,在一幅长70cm,宽50cm的风景画四周镶上一条宽度相同的金色纸边,制成一幅挂画.如果要使金色纸边的面积是1300cm2,求金色纸边的宽度.
某商店6月份的利润是2500元，要使8月份的利润达到3600元，平均每月增长的百分率是多少？
则:7月份比6月份利润增长________ 元. 7月份的利润是 _______________元 8月份比7月份利润增长____________ 元 8月份的利润是 ____________ 元
2500(1+x) ·x
2500(1+x)+2500(1+x) ·X= 2500(1+x)2
如果设平均每个月增长的百分率为x
设平均每个月增长的百分率是x.根据题意得:
2500(1+x)2 =3600
(1+x)2= 1.44
x1=0.2=20％ x2=-2.2
答:平均每个月增长的百分率是20％.
1.两次增长后的量=原来的量(1+增长率)2若原来为a,平均增长率是x,增长后的量为b 则 第1次增长后的量是 a(1+x) =b 第2次增长后的量是 a(1+x)2=b … 第n次增长后的量是 a(1+x)n=b
2.反之，若为两次降低，则 平均降低率公式为
3.平均增长(降低两次率)公式
4.注意:(1) 1与x的位置不要调换
(2) 解这类问题用 直接开平方法
某蔬菜交易市场2月份的蔬菜交易量是5000t，4月份达到7200t，平均每月增长的百分率是多少？
解：设平均每月增长的百分率是x.根据题意得：
5000（1+x）2=7200
(1+x)2=1.44
x1=0.2=20％ x2=-2.2
答:平均每个月增长的百分率是20％
1。某种服装原价为每件80元,经两次降价,现售价为每件51.2元,求平均每次降价的百分率.
2。一张长方形铁皮，四个角各剪去一个边长为4cm的小正方形，再折起来做成一个无盖的小 盒子。已知铁皮的长是宽的2倍，做成的小盒子的容积是1536cm3，求长方形铁皮的长与宽 。
某服装店花2000元进了批服装，按50%的利润定价，无人购买。决定打折出售，但仍无人购买，结果又一次打折后才售完。经结算，这批服装共盈利430元。如果两次打折相同，每次打了几折？
1.某厂1月份生产零件2万个，一季度共生产零件7.98万个，若每月的增长率相同，求每月的增长率.
2.某公司计划两年内把产量翻两番，如果每年比上一年提高的百分数相同，求这个百分数。