人教版八年级下册第十六章 二次根式综合与测试巩固练习
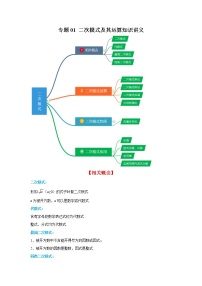
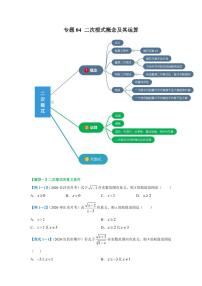
展开专题01 二次根式及其运算知识讲义
【相关概念】
二次根式:
形如(a≥0)的式子叫做二次根式.
a为被开方数,a可以是数字或代数式.
代数式:
含有字母的数学表达式称为代数式.
整式、分式均为代数式.
最简二次根式:
1、被开方数中不含能开得尽方的因数或因式;
2、被开方数的因数是整数,因式是整式.
同类二次根式:
几个二次根式化成最简二次根式后,如果被开方数相同,这几个二次根式叫做同类二次根式.
【二次根式运算】
乘法
(a≥0,b≥0)
除法
(a≥0,b>0)
加(减)法
先把各根式化成最简根式,再合并同类根式
分母有理化
【二次根式性质】
双重非负性:≥0,a≥0
非负数:|a|,a2n,
【二次根式应用】
因式的内移和外移:
(1)负号不能移到根号下;(2)根号下的负号不能移到根号外.
【题型一】二次根式有意义条件
例1. (2020·河北承德市期末)若有意义,则m能取的最小整数值是( )
A.m = 0 B.m = 1 C.m = 2 D.m = 3
例2. (2020·上海市静安区)如果,那么x的取值范围是_______.
例3.(2019·北京期末)如果,那么的取值范围是______.
【题型二】同类二次根式
例4. (2020·上海市期中)如果二次根式与是同类二次根式,那么满足条件的中最小正整数是________.
例5. 若两个最简二次根式与能够合并,则_________.
例6. 最简二次根式与是同类二次根式,则=________.
【题型三】变式考查
例7. (2020·浙江宁波市期中)我们把形如(a,b为有理数,为最简二次根式)的数叫做型无理数,如是型无理数,则是( )
A.型无理数 B.型无理数 C.型无理数 D.型无理数
例8. (1)已知是整数,求自然数所有可能的值;
(2)已知是整数,求正整数的最小值.
例9.(2020·四川武外月考)若,则x=__________.
【题型四】二次根式运算
例10.(2020·南通市月考)一个等腰三角形两边的长分别为和,则这个三角形的周长为( )
A. B.
C.或 D.无法确定
例11.计算:.
例12.(2020·福建省泉州月考)已知,x的整数部分为a,小数部分为b,求的值.
例13.(2020·广东佛山市月考)先阅读,再解答:由 可以看出,两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式,在进行二次根式计算时,利用有理化因式,有时可以化去分母中的根号,例如:
,请完成下列问题:
(1)的有理化因式是 ;
(2)化去式子分母中的根号: .(直接写结果)
(3) (填或)
(4)利用你发现的规律计算下列式子的值:
例14. 若a,b都是正整数,且a<b,与是可以合并的二次根式,是否存在a,b,使+=?若存在,请求出a,b的值;若不存在,请说明理由.
例15.(2019·辽宁大连市期中)[观察]请你观察下列式子的特点,并直接写出结果:
;
;
;
……
[发现]根据你的阅读回答下列问题:
(1)请根据上面式子的规律填空:
(n为正整数);
(2)请证明(1) 中你所发现的规律.
[应用]请直接写出下面式子的结果:
.
【题型五】化简求值
例16. (2021·江苏南通市期末)化简的结果是( )
A. B. C. D.1
例17.(2020·浙江杭州期中)实数a,b在数轴上的位置如图,则化简的结果为( )
A. B. C. D.
例18.若数轴上表示数的点在原点的左边,则化简的结果是( )
A. B. C. D.
例19.(2020·温州月考)下列四个式子中,与的值相等的是( )
A. B. C. D.
例20.下列给出的四个命题:
①若 ,则;②若a2﹣5a+5=0,则 ;
③
其中是真命题是
【题型六】阅读材料
例21.(2021·北京延庆区期末)我们规定用(a,b)表示一对数对.给出如下定义:记,,其中(a > 0,b > 0),将(m,n)与(n,m)称为数对(a,b)的一对“对称数对”.
例如:(4,1)的一对“对称数对”为(,1)和(1,);
(1)数对(9,3)的一对“对称数对”是 ;
(2)若数对(3,y)的一对“对称数对”相同,则y的值为 ;
(3)若数对(x,2)的一个“对称数对”是(,1),则x的值为 ;
(4)若数对(a,b)的一个“对称数对”是(,),求ab的值.
例22. 阅读理解:
二次根式的除法,要化去分母中的根号,需将分子、分母同乘以一个恰当的二次根式.
例如:化简.
解:将分子、分母同乘以得:.
类比应用:
(1)化简: ;
(2)化简: .
拓展延伸:
宽与长的比是的矩形叫黄金矩形.如图①,已知黄金矩形ABCD的宽AB=1.
(1)黄金矩形ABCD的长BC= ;
(2)如图②,将图①中的黄金矩形裁剪掉一个以AB为边的正方形ABEF,得到新的矩形DCEF,猜想矩形DCEF是否为黄金矩形,并证明你的结论;
(3)在图②中,连结AE,则点D到线段AE的距离为 .
例23. (2019·四川月考)阅读下列材料,然后回答问题.
①在进行二次根式的化简与运算时,我们有时会碰上如一样的式子,其实我们还可以将其进一步化简: 以上这种化简的步骤叫做分母有理化.
②学习数学,最重要的是学习数学思想,其中一种数学思想叫做换元的思想,它可以简化我们的计算,比如我们熟悉的下面这个题:已知 ab2,ab 3 ,求 a2 b2 .我们可以把ab和ab看成是一个整体,令 xab , y ab ,则 a 2 b2 (a b)2 2ab x2 2y 4 610.这样,我们不用求出a,b,就可以得到最后的结果.
(1)计算:
(2)已知 m 是正整数, a ,b 且 2a2 1823ab 2b2 2019 .求 m.
(3)已知,则的值为
例24.(2020·湖南怀化市期末)同学们,我们以前学过完全平方公式,你一定熟练掌握了吧!现在,我们又学习了二次根式,那么所有的非负数(以及0)都可以看作是一个数的平方,如,,下面我们观察:,反之,,∴,∴
求:(1);
(2);
(3)若,则m、n与a、b的关系是什么?并说明理由.
例25.(2020·安徽安庆市)阅读理解题,下面我们观察:
反之,
所以,所以
完成下列各题:
(1)在实数范围内因式分解:;
(2)化简:;
(3)化简:.
2021学年第十七章 勾股定理综合与测试课时训练: 这是一份2021学年第十七章 勾股定理综合与测试课时训练,文件包含专题03二次根式及勾股定理中的数学思想方法讲义解析版docx、专题03二次根式及勾股定理中的数学思想方法讲义原卷版docx等2份试卷配套教学资源,其中试卷共52页, 欢迎下载使用。
数学17.1 勾股定理课后练习题: 这是一份数学17.1 勾股定理课后练习题,文件包含专题02勾股定理四大核心知识讲义解析版docx、专题02勾股定理四大核心知识讲义原卷版docx等2份试卷配套教学资源,其中试卷共63页, 欢迎下载使用。
初中数学人教版八年级下册第十六章 二次根式综合与测试课后练习题: 这是一份初中数学人教版八年级下册第十六章 二次根式综合与测试课后练习题,文件包含专题01二次根式及其运算知识基础巩固+技能提升解析版docx、专题01二次根式及其运算知识基础巩固+技能提升原卷版docx等2份试卷配套教学资源,其中试卷共32页, 欢迎下载使用。