高中数学人教A版 (2019)必修 第一册1.3 集合的基本运算教课ppt课件

这是一份高中数学人教A版 (2019)必修 第一册1.3 集合的基本运算教课ppt课件，共18页。PPT课件主要包含了知识探究一，“并”的含义，②x仅属于集合B，①x仅属于集合A，③x既属于A又属于B，自然语言，符号语言，图形语言，知识探究二，并集的性质等内容，欢迎下载使用。

我们知道，实数有加、减、乘、除等运算。类比于实数，集合是否也有类似的运算呢？
问题1：考察下列各个集合，类比实数的加法运算，你能说出集合C与集合A，B之间的关系吗？ （1）A={1，3，5}，B={2，4，6}， C={1，2，3，4，5，6}； （2）A={x｜x是有理数}，B={x｜x是无理数}， C={x｜x是实数}。
这时我们把集合C叫集合A与集合B的并集。
　 集合C中的元素来自集合A，或者来自A集合a或者同时来来自B。即 集合C是由集合A和集合B的元素合并后组成的。
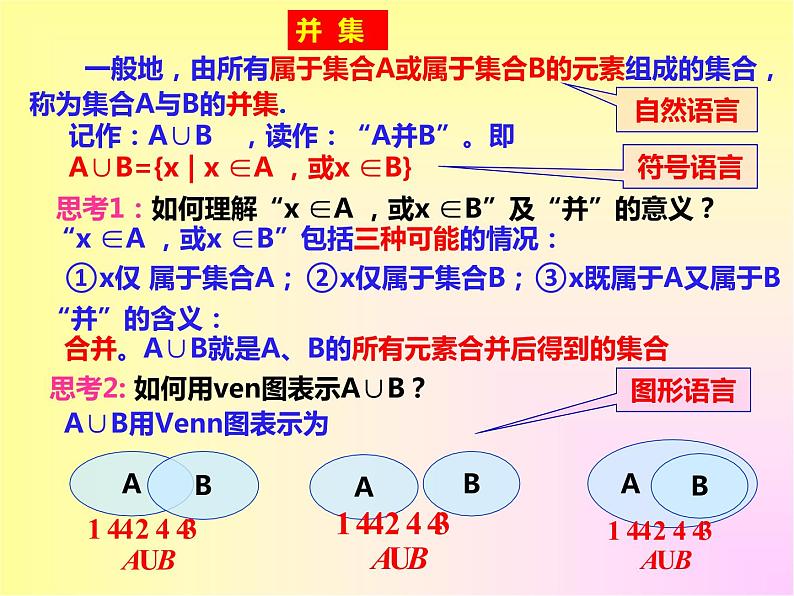
一般地，由所有属于集合A或属于集合B的元素组成的集合，称为集合A与B的并集. 记作：A∪B　，读作：“A并B”。即 A∪B={x | x ∈A ，或x ∈B}
“x ∈A ，或x ∈B”包括三种可能的情况：
思考1：如何理解“x ∈A ，或x ∈B”及“并”的意义？
A∪B用Venn图表示为
思考2: 如何用ven图表示A∪B？
合并。A∪B就是A、B的所有元素合并后得到的集合
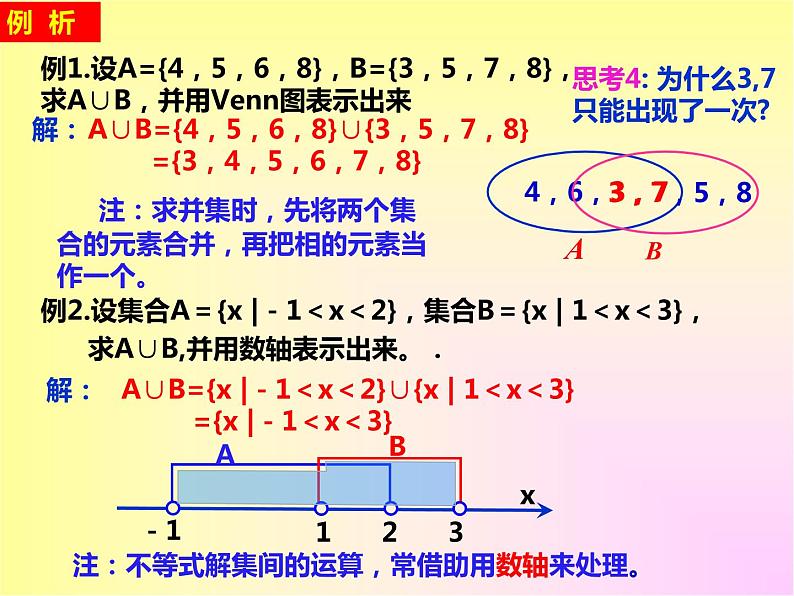
例1.设A={4，5，6，8}，B={3，5，7，8}，求A∪B，并用Venn图表示出来
A∪B={4，5，6，8}∪{3，5，7，8} ={3，4，5，6，7，8}
注：求并集时，先将两个集合的元素合并，再把相的元素当作一个。
例2.设集合A＝{x |－1＜x＜2}，集合B＝{x | 1＜x＜3}， 求A∪B,并用数轴表示出来。．
A∪B={x |－1＜x＜2}∪{x | 1＜x＜3} ={x |－1＜x＜3}
注：不等式解集间的运算，常借助用数轴来处理。
思考4: 为什么3,7只能出现了一次?
　　思考３: (1)集合A、B与集合A∪B的关系如何？ A∪B与B∪A的关系如何？
　　问题2：考察下列两组集合，说说集合A、B和集合C的元素有什么关系：（1）A={2，4，6，8，10}, B={3，5，8，12}， C={8}；（2）A={x|x是本校在校的女生}，B={x|x是本校在校的高一年级的女生} ， C={x|x是本校在校的高一年级的女生} 　　
集合C中的元素既属于集合A又属于集合B，即集合C是由集合A和集合B的公共元素组成的。
思考1：集合A-集合B=集合C吗？
类比于实数的减法，集合的差运算中学阶段不涉及
思考2：集合C中的元素在集合A中吗？在集合B中吗？
这时我们把集合C叫集合A与集合B的交集。
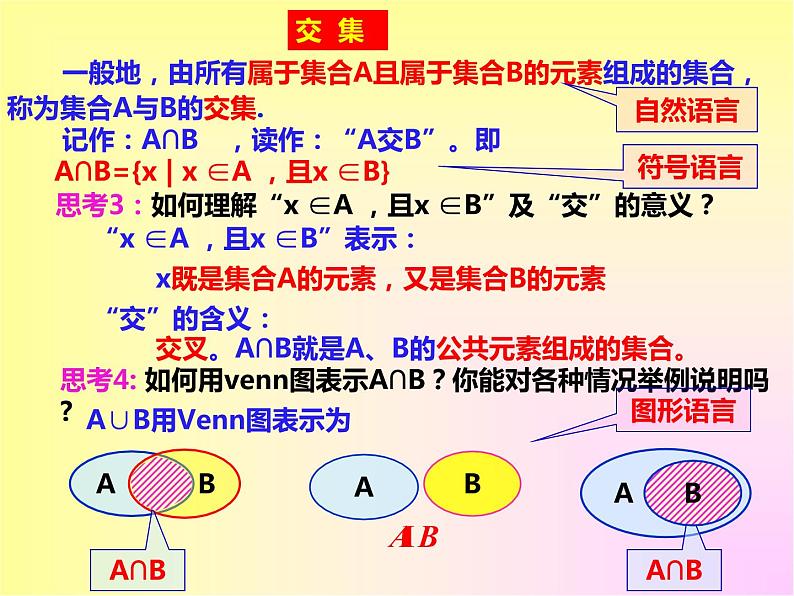
一般地，由所有属于集合A且属于集合B的元素组成的集合，称为集合A与B的交集. 记作：A∩B　，读作：“A交B”。即 A∩B={x | x ∈A ，且x ∈B}
“x ∈A ，且x ∈B”表示：
思考3：如何理解“x ∈A ，且x ∈B”及“交”的意义？
思考4: 如何用venn图表示A∩B？你能对各种情况举例说明吗?
交叉。A∩B就是A、B的公共元素组成的集合。
x既是集合A的元素，又是集合B的元素
平面内的两条直线有三种上可能的关系： 平行，相交或重合当两条直线 l1、l2平行时， L1∩L2=Φ；当两条直线 l1、l2相交于一点P时， L1∩L2={点P}；当两条直线 l1、l2重合时， L1∩L2= L1=L2。
例3.设L1,L2分别是平面内两条直线 l1和 l2上点的集合，试用集合的运算表示这两条直线的位置关系。
例4. 本校开运动会。设 A＝{x |x是本校高一年级参加百米赛的同学}， B＝{x |x是本校高一年级参加跳高比赛的同学}， 求A∩B.
∴A∩B={x |本校高一年级中即参加百米赛又参加跳高比赛的同学}。
A∩B是由本校高一年级中即参加百米赛，又参加跳高比赛的同学组成的集合。
思考5: 下列各式是否成立？为什么，你能举例说明吗？
1.设A={3，5，6，8}，B={4，5，7，8}。求A∩B，A∪B。
2.设A={x|x2-4x-5=0}，B={x|x2=1}。求A∩B，A∪B。
3.设A={x|x是等腰三角形}，B={x|x是直角三角形}。 求A∩B，A∪B
4.设A={x|x是幸福农场的汽车}，B={x|x是幸福农场的拖拉机}。 求A∩B，A∪B
A∪B={3，4，5，6，7，8}
A={x|x2-4x-5=0}
A∪B={-1，1，5，}
A∩B={x|x是等腰直角三角形}
A∪B={x|x是等腰三角形或直角三角形}
A∪B={x|x是是幸福农场的汽车或拖拉机}
5.设A=N，B=Q。求A∩B，A∪B
例5.求下列各组中两集合的交集和并集
例6. 已知集合A={-2,2,a2}，B={1,a}，若A∩B={1}，求a.
B={1,1}，不满足集合元素的互异性。
A={-2，2，1}，B={1，-1}，
思考：若将“A∩B={1}”改为“A∪B={-2,1,2,a}”,则结果又如何？
由A∪B={-2,1,2,a}得
∵a=1时，B={1,1}不满足集合元素的互异性
1.从自然语言、符号语言和图形语言和不同的角度说一说什么是集合A、B的交集 .
2.集合A、B的交集哪些性质？
3.从自然语言、符号语言和图形语言和不同的角度说一说什么是集合A、B的并集 .
4.集合A、B的并集哪些性质？
5.进行集合的交集、并集等运算时要注意哪些问题？
（1）先将能化简的集合进行化简；
（2）必要时可借助于图形语言（如Venn图、数轴等）。