初中数学人教版七年级上册1.2.4 绝对值教课课件ppt

这是一份初中数学人教版七年级上册1.2.4 绝对值教课课件ppt，文件包含124绝对值pptx、124绝对值docx等2份课件配套教学资源，其中PPT共33页， 欢迎下载使用。

绝对值绝对值的非负性比较有理数的大小
1. 定义一般地，数轴上表示数a的点与原点的距离叫做数a的绝对值，记作| a |. 读作“a的绝对值”.
由于绝对值是两点间的距离，所以绝对值不可能是负数.
2. 性质一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0. a(a > 0)，即：|a|= 0 (a=0)，－a(a < 0).
特别提醒由绝对值的定义可知：一个数对应的点离原点越近，它的绝对值越小，离原点越远，它的绝对值越大，所以没有绝对值最大的数，只有绝对值最小的数为0.
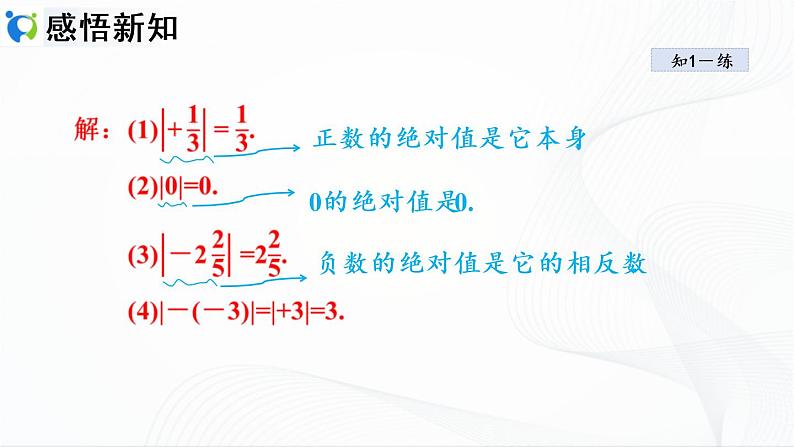
解题秘方：紧扣绝对值的性质进行计算.
正数的绝对值是它本身.
负数的绝对值是它的相反数.
技巧点拨：求一个数的绝对值的方法要求一个数的绝对值，首先判断这个数是正数、负数还是零，然后求出该数的绝对值. 要确保其结果为非负数且只有一个.
若|x|=2 022，则x=________.
解题秘方：根据绝对值的几何意义可知，数轴上表示数x的点与原点的距离为2 022 个单位长度，即可确定x的值.
2-1. 若| －m | =2 023，则m= ________.
2-2. 若| x－2 |=2， 则x=_______.
1. 任何一个数的绝对值，都是唯一的非负数 .2. 绝对值是它本身的数是非负数，绝对值是它的相反数的数是非正数，0 是绝对值最小的数，即：若| a | ＝ a，则a ≥ 0，若| a |=－a，则a ≤ 0.3. 绝对值相等的两个数相等，或互为相反数，即：若| a |=| b |，则a=b 或a=－b.
特别提醒绝对值的非负性是绝对值的一个重要性质，即对于任意有理数a，都有| a | ≥ 0.1.当a≠0时，| a |＞0，当a=0 时，| a |=0.2. 当| a | ＞ 0 时，a≠0，当| a |=0时，a=0.
下列各式中无论m为何值，一定是正数的是( )A．|m| B．|m+1| C．| m |+1 D．－(－m)
解题秘方：紧扣绝对值的非负性进行判断.
解：选项A中，当m=0 时，不符合题意；选项B中，当m=－1 时，| m+1 |=0，不符合题意；选项D中，－(－m)=m，显然不符合题意；选项C中，因为| m | ≥ 0，所以| m |+1 ≥ 1，符合题意.
3-1. 若a为任意有理数， 则－｜－a｜一定是( )A．负数或零 B．负数C．正数或零 D．正数
3-2. 式子| m－3 | + 6的值随m的变化而变化，当m= ______时，| m－3 | +6 有最小值，最小值是______.
如果a=－4，且| a | = | b |，求| b+4 | 的值.
解题秘方：紧扣“若|x|=a(a>0），则x=±a”进行求解.
解：因为a=－4，所以|b|=|a|=|－4|=4.所以b=4 或b=－4.当b=4 时，|b+4|=|4+4|=8；当b=－4 时，|b+4|=|－4+4|=0.所以|b+4| 的值是8 或0.
易漏掉“－4”这种情况.
4-1. 如果｜ x ｜ =| －5 |，那么x 等于( )A．5 B．－5C．±5 D．以上都不对
1. 用数轴比较有理数大小的法则数学中规定：在数轴上表示有理数，它们从左到右的顺序就是从小到大的顺序. 即：右边的数总比左边的数大.
2. 用数的性质比较有理数大小的法则(1)正数大于0，0 大于负数，正数大于负数.(2)两个负数，绝对值大的反而小.即：
特别提醒利用数轴比较大小的优点：一是直接看表示数的点在数轴上的位置即可；二是一次可以比较多个数.
解题秘方：把这些数准确地表示在同一条数轴上，按右边的点表示的数大于左边的点表示的数，将各数按从小到大的顺序排列.
5-1. 如图，a 与b 的大小关系是( )A．abC．a=b D．b=2a
5-2. 若a解题秘方：利用正数>0> 负数，两个负数，绝对值大的反而小进行比较.
6-1. 下列选项中， 比－2℃低的温度是( )A．－3℃ B．－1℃C．0℃ D．1℃
－|－7|<－(＋5.3)．