初中数学21.3 实际问题与一元二次方程精品课件ppt

人教版初中数学九年级上册

21.3.4实际问题与一元二次方程（四）图形面积问题教学设计

一、教学目标：

1.掌握面积法建立一元二次方程的数学模型.（难点）

2.能运用一元二次方程解决与面积有关的实际问题.（重点）

二、教学过程：

复习回顾

1.矩形的长和宽分别为a m和b m，则其面积为____m2，周长为_______m.
2.梯形的上、下底分别为a cm和b cm，高为h cm，则其面积为__________cm2.
3.圆的半径为r cm，则其面积为____cm2，周长为____cm.
4.长方体的长、宽、高分别是a cm，b cm和c cm，则其体积为_____cm3.
5.直角三角形的两直角边长分别为a cm和b cm，斜边长为c cm，则a，b，c之间的数量关系为_________.

练一练

现有长19cm，宽15cm的矩形硬纸片，将它的四角各剪去一个同样大小的正方形后，再折成一个无盖的纸盒，要使纸盒的底面积为117cm2，问剪去的小正方形的边长应是多少？

解：设剪去的小正方形的边长为xcm，则盒底的长为(19-2x)cm，宽为(15-2x)cm，依题意得

(19-2x)(15-2x)=117

整理得 x2-17x+42=0

解得 x1=3，x2=14(不合题意，舍去)

答：剪去的小正方形的边长应为3cm.

知识精讲

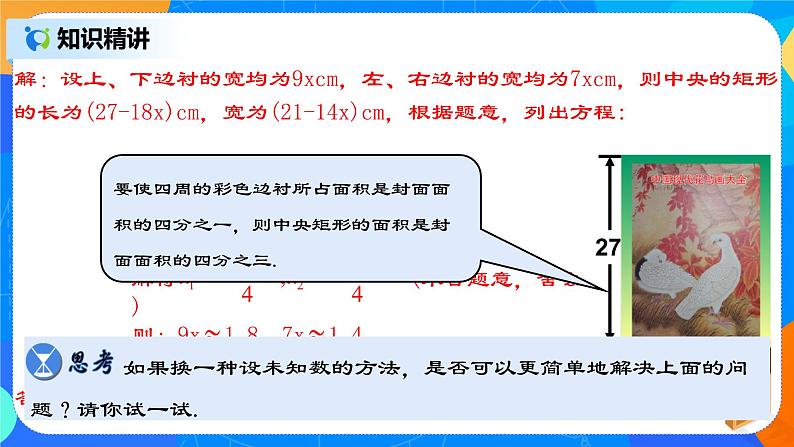
探究：如图，要设计一本书的封面，封面长27cm，宽21cm，正中央是一个与整个封面长宽比例相同的矩形.如果要使四周彩色的边衬所占面积是封面面积的四分之一，上、下边衬等宽，左、右边衬等宽，应如何设计四周边衬的宽度(结果保留小数点后一位)？

分析：封面的长宽之比是27:21=9:7，中央的矩形的长宽之比也应是9:7.设中央矩形的长和宽分别是9a cm和7a cm，由此得上、下边衬与左、右边衬的宽度之比是

(27-9a): (21-7a)=9(3-a):7(3-a)=9:7

解：设上、下边衬的宽均为9x cm，左、右边衬的宽均为7x cm，则中央的矩形的长为(27-18x)cm，宽为(21-14x)cm，根据题意，列出方程

(27-18x)(21-14x)= ×27×21

整理，得 16x2-48x+9=0

解得 x1=，x2=(不合题意，舍去)

则：9x≈1.8，7x≈1.4.

答：上、下边衬的宽约为1.8cm，左、右边衬的宽约为1.4cm.

思考:如果换一种设未知数的方法，是否可以更简单地解决上面的问题？请你试一试.

解：设中央的矩形的长、宽分别为9y cm、7y cm，根据题意，列出方程

9y·7y=×27×21

整理，得 y2=

解得 y1=，y2= (不合题意，舍去)

则：(27-9y)≈1.8， (21-7y)≈1.4.

答：上、下边衬的宽约为1.8cm，左、右边衬的宽约为1.4cm.

典例解析

例1.如图，某小区规划在长32米，宽20米的矩形场地ABCD上修建三条同样宽的3条小路，使其中两条与AB平行，一条与AD平行，其余部分种草，若使草坪的面积为570米2，问小路应为多宽?

【分析】平移法---化零为整

解：设小路的宽为x米，依题意得：

(32-2x)(20-x)=570

整理，得x2-36x+35=0

解得 x1=1,x2=35(不符合题意，舍去)

答：小路的宽为2米.

【针对练习】

如图，在宽为20m，长为30m的矩形地面上修筑同样宽的道路（图中阴影部分），余下的部分种上草坪，要使草坪的面积为551m2，求道路的宽．

解：设道路的宽为，根据题意得：

，

解得：，（不合题意，舍去），

答：道路的宽为．

例2.《生物多样性公约》缔约方大会第十五次会议于2021年10月11日至15日和2022年上半年分两阶段在昆明召开．为迎接cop15，昆明某园艺公司准备围建一个矩形花圃，其中一边靠墙（墙长20米），另外三边用篱笆围成如图所示，所用的篱笆长为36米．

(1)设垂直于墙的一边长为x米．则平行于墙的一边为_________米；

(2)当花圃的面积为144平方米时，求垂直于墙的一边的长为多少米？

(1)设垂直于墙的一边长为x米，则平行于墙的一边为36-2x米；

(2)设花圃的面积为S平方米

∴S=（36-2x）·x=144

解得x=12

答：当花圃的面积为144平方米时，求垂直于墙的一边的长为12米．

【针对练习】

如图，学校建一长方形自行车棚，一边靠墙（墙长18米），另三边用总长50米的栏杆围成，留2米宽的门，若想建成面积为240平方米的自行车棚，则车棚垂直于墙的一边的长为多少米？

解：设车棚垂直于墙的一边的长为x米，则平行于墙的一边的长为米，

由题意列方程可得：，

解得或x=6

当车棚垂直于墙的一边的长为6米时，平行于墙的一边的长为40米，大于墙长的18米，

答：车棚垂直于墙的一边的长为20米.

例3.如图，有一张长6cm、宽5cm的矩形铁皮，将其剪去两个全等的正方形和两个全等的矩形，用剩余（阴影）部分可制成底面积为6cm2的有盖长方体铁盒．求剪去的正方形的边长．

设剪去的正方形的边长为xcm，则底面的长为（5﹣2x）cm，宽为﹣x＝（3﹣x）cm，

依题意得：（5﹣2x）（3﹣x）＝6，

整理得：2x2﹣11x+9＝0，

解得：x1＝1，x2＝，

当x＝1时，5﹣2x＝3，3﹣x＝2，符合题意；

当x＝时，5﹣2x＝﹣4＜0，不合题意，舍去．

答：剪去的正方形的边长为1．

【针对练习】

我市在创建全国文明城市期间，对一个矩形广场进行扩建改造．如图，原广场长为30m、宽为20m，要求扩充后的矩形广场长与宽的比为4：3．扩充区域的扩建费用每平方米30元，扩建后在原广场和扩充区域都铺设地砖，铺设地砖费用每平方米100元．如果计划总费用606000元，扩充后广场的长和宽应分别是多少米？

解：设扩充后广场的长为4xm，宽为3xm，

依题意得：4x•3x•100+30（4x•3x﹣30×20）＝606000．

解得x1＝20，x2＝﹣20（舍去）．

所以4x＝80，3x＝60，

答：扩充后广场的长为80m，宽为60m．

课堂小结

1.本节课你有哪些收获？2.还有没解决的问题吗？

达标检测

1.某学校准备修建一个面积为200平方米的矩形花圃，它的长比宽多10米，设花圃的宽为x米，则可列方程为(   )

A.x(x-10)=200        B.2x+2(x-10)=200

C.x(x+10)=200        D.2x+2(x+10)=200

2.在一幅长为80cm,宽为50cm的矩形风景画的四周镶一条相同宽度的金色纸边,制成一幅矩形挂图，如图所示，如果要使整个挂图的面积是5400cm2，设金色纸边的宽为xcm,那么x满足的方程是(   )

A.(80+x)(50+x)=5400            B.(80+2x)(50+x)=5400

C.(80+x)(50+2x)=5400           D.(80+2x)(50+2x)=5400

3.一个直角三角形的斜边长为√20，一直角边长是另一直角边长的2倍，则这个直角三角的面积是(   )

A.3       B.4         C.5        D.6

4.用22cm长的铁丝，折成一个面积是30cm2的矩形，求这个矩形的长和宽.又问：能否折成面积是32cm 2的矩形呢？为什么？

5.如图，小华要为一个长6分米，宽4分米的长方形防疫科普电子小报四周添加一个边框，要求边框的上下左右宽度相等，且边框面积与电子小报内容所占面积相等．求小华添加的边框的宽度．

6.如图，矩形ABCD是景区内一块油菜花地，AB=6m，BC=8m，点E、F、G、H分别在矩形的四条边上，且AE=FC=CG=HA，现在其中修建一条观花道（阴影所示）供游人赏花．若观花道的面积为13m2，求AE的长．

三、教学反思：

    与图形有关的问题是一元二次方程应用的常见题型，解决这类问题的关键是将不规则图形分割或补全成规则图形，找出各部分面积之间的关系，运用面积等计算公式列出方程，对图形进行分割或补全的原则，转化成为规则图形时越简单越直观越好.