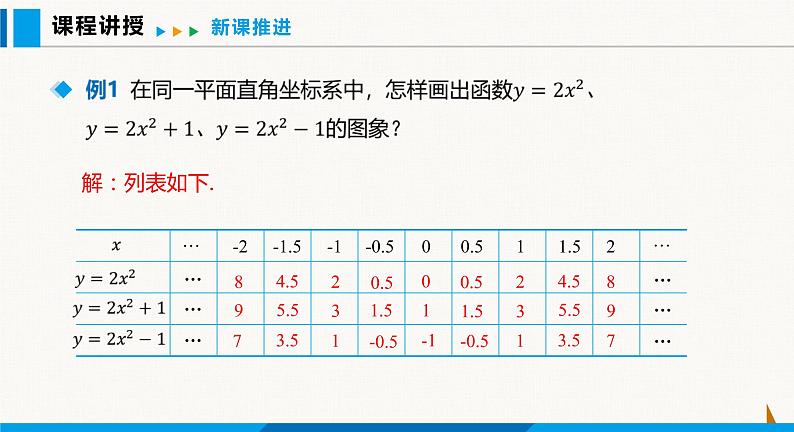
初中数学沪科版九年级上册21.2 二次函数的图象和性质教案配套ppt课件

这是一份初中数学沪科版九年级上册21.2 二次函数的图象和性质教案配套ppt课件，共21页。PPT课件主要包含了学习目标及重难点，课程导入，课程讲授，新课推进，解列表如下，y2x2+1，y2x2，y2x2-1，0-1，二次函数等内容，欢迎下载使用。

还记得通过什么方法画出抛物线y= ax2的图象吗
还记得抛物线y= ax2的性质吗
（2）当a>0时，抛物线的开口向上，顶点是抛物线的最低点;
当a<0时，抛物线的开口向下，顶点是抛物线的最高点.
（3）|a|越大，抛物线的开口越小.
（1）抛物线y= ax2的对称轴是y轴，顶点是原点.
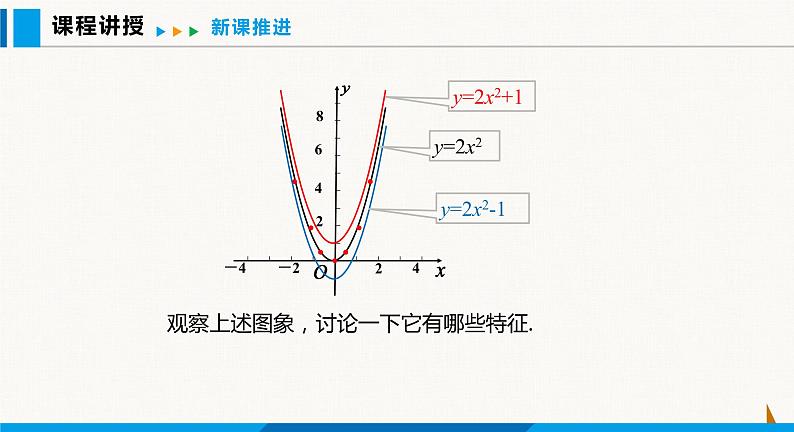
观察上述图象，讨论一下它有哪些特征.
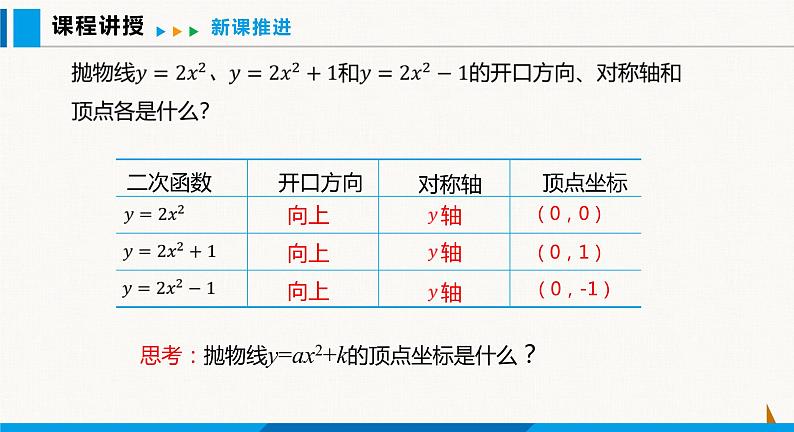
思考：抛物线y=ax2+k的顶点坐标是什么？
抛物线 y＝ax2＋k与抛物线 y＝ax2 有什么关系？
根据例2的图象，思考并填空：
例3 在同一直角坐标系中，一次函数y＝ax＋k和二次函数y＝ax2＋k的图象大致为(　　)
总结：熟记一次函数y＝kx＋b在不同情况下所在的象限，以及熟练掌握二次函数的有关性质(开口方向、对称轴、顶点坐标等)是解决问题的关键．
1、已知（m,n)在y=ax2+a（a不为0）的图象上，(-m,n) ___（填“在”或“不在”）y=ax2+a（a不为0）的图象上.2、若y=x2+（k-2）的顶点是原点，则k____；若顶点位于x轴上方，则k____；若顶点位于x轴下方，则k .
二次函数y=ax2+k的图象可以由 y=ax2 的图象平移得到当k > 0 时,向上平移k个单位长度得到.当k < 0 时,向下平移-k个单位长度得到.
上下平移规律：平方项不变，常数项上加下减.
二次函数 y=ax2 与 y=ax2+k（a ≠ 0）的图象的关系
习题1 二次函数y＝－3x2＋1的图象是将(　　) A．抛物线y＝－3x2向左平移3个单位得到 B．抛物线y＝－3x2向左平移1个单位得到 C．抛物线y＝3x2向上平移1个单位得到 D．抛物线y＝－3x2向上平移1个单位得到
解析：二次函数 y＝－3x2＋1的图象是将抛物线 y＝－3x2向上平移1个单位得到的．故选D.
不画函数y=-x2和y=-x2+1的图象回答下面的问题：
（1）抛物线y=-x2+1经过怎样的平移才能得到抛物线y=-x2.
（2）函数y=-x2+1，当x 时， y随x的增大而减小；当x 时，函数y有最大值，最大值y是 ，其图象与y轴的交点坐标是 ，与x轴的交点坐标是 .
（3）试说出抛物线y=x2-3的开口方向、对称轴和顶点坐标.
(-1,0),(1,0)
开口方向向上，对称轴是y轴，顶点坐标（0，-3）.
习题3 1、对于二次函数y=(m+1)xm2-m+3,当x>0时，y随x的增大而增大，则m=____.2、已知二次函数y=(a-2)x2+a2-2的最高点为（0，2）， 则a=____.3、抛物线y=ax2+c与x轴交于A（-2,0）﹑B两点，与y轴交于点C(0，-4),则三角形ABC的面积是_______.
习题4 如图，抛物线y＝x2－4与x轴交于A、B两点，点P为抛物线上一点，且S△PAB＝4，求P点的坐标．
解：抛物线y＝x2－4，令y＝0，得到x＝2或-2，即A点的坐标为(-2，0)，B点的坐标为(2，0)，∴AB＝4.∵S△PAB＝4，设P点纵坐标为b，∴ ×4|b|＝4，∴|b|＝2，即b＝2或－2.当b＝2时，x2－4＝2，解得x＝± ，此时P点坐标为( ，2)，(- ，2)；当b＝-2时，x2－4＝-2，解得x＝± ，此时P点坐标为( ，-2)，(- ，-2)．