





数学七年级上册第4章 图形的认识4.2 线段、射线、直线教课内容课件ppt
展开图中可以近似地看做线段、射线、直线的分别有哪些?
绷紧的钢拉索、笔直的路灯杆等实物都给我们以线段的形象,线段有两个端点.线段向一端无限延长形成了射线,射线有一个端点.线段向两端无限延长形成了直线,直线没有端点.
生活中有哪些事物可以作为直线、射线、线段的原型?试举例说明.
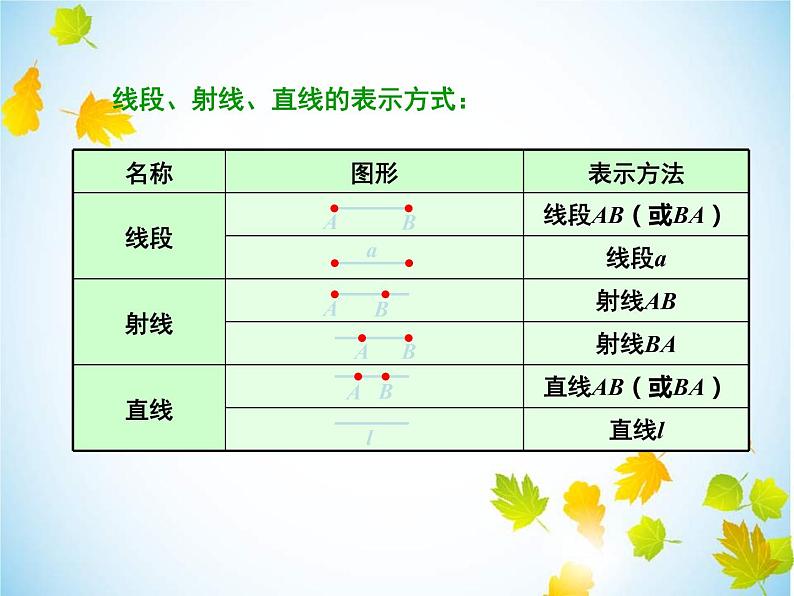
线段、射线、直线的表示方式:
一条线段向两端无限延长就得到一条直线,这说明一条直线有两个方向,它们是互为相反的方向,取定一个方向,就确定了另一个方向.
如图中的直线AB,一个是从A到B的方向,一个是从B到A的方向.
例如,把一条笔直的自行车专用道看成一条直线,那么自行车专用道就有两个互为相反的方向.
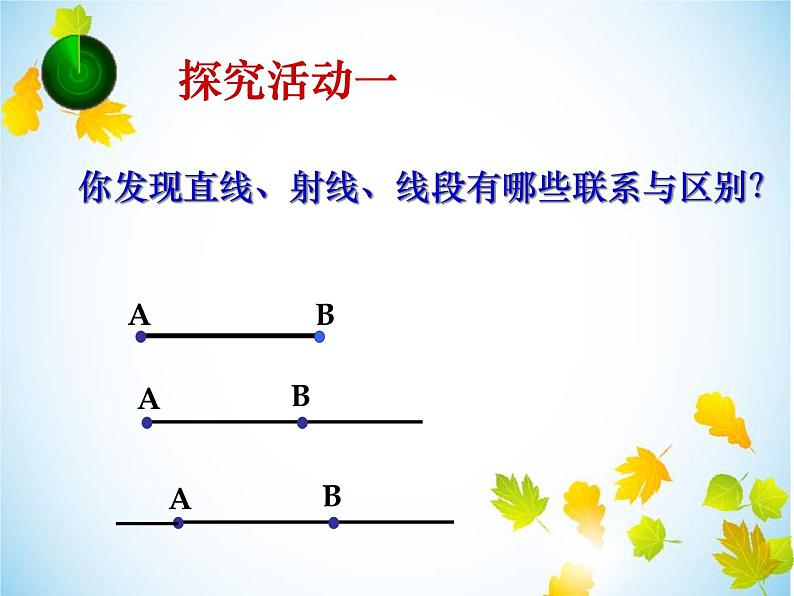
你发现直线、射线、线段有哪些联系与区别?
线段向一端无限延长形成射线,向两端无限延长形成直线
二、直线、射线、线段的区别与联系:
射线、线段都是直线的一部分.
1.射线是直线的一部分. ( )2.线段是射线的一部分. ( )3.画一条射线,使它的长度为3cm. ( )4.线段AB和线段BA是同一条线段. ( )5.射线OP和射线PO是同一条射线. ( )6.如图,画一条线段ab. ( )
动手画一画,点与直线有哪几种位置关系?
点与直线有两种位置关系:点在直线上或点在直线外,也可以说直线经过这个点或直线不经过这个点.
如图,点P在直线l上(直线l经过点P),
点Q 在直线l外(直线l不经过点Q).
当两条不同的直线只有一个公共点时,我们称这两条直线相交,这个公共点叫做它们的交点.
如图,直线l1与l2相交于点O.
1.如果你想将一根细木条固定在墙上,至少需要几个钉子?
2.过一点A可以画几条直线?3.过两点A,B可以画几条直线?
过两点有且只有一条直线.
植树时,只要定出两个树坑的位置,就能确定同一行的树坑所在的直线.
(1)画一条2cm的射线.
(2)如图,直线 AB和直线AC表示的是同 一条直线.
(3)如上图,射线BA和射线BC表示的是同一条射线.
一.判断下列说法是否正确.
(1)直线EF经过点C;
二. 按下列语句画出图形.
(2)经过点O的三条线段a,b,c;(3)线段AB,CD相交于点B.
• 点与直线的位置关系
• 直线 、射线 、线段的表示方法
• 对线段、射线、直线的认识
• 直线、射线、线段的联系与区别
4.2 线段、射线、直线
第2课时 线段的长短比较
问题:怎样比较两条线段的长短呢?
你能再举出一些比较线段长短的实例吗?
你能从上面活动得到一些启发吗?
比较两根细木条(或绳子)的长短
A B C D
点A与点C重合,点B落在C,D之间,这时我们说线段AB小于CD,记作AB<CD.
想一想,什么情况下线段AB大于线段CD,线段AB等于线段CD?
(也可以先测量出线段的长度,再比较.)
1.用圆规截取的方法比较图中下列两组线段的大小:
(1) AC 和AB; (2) BC 和AB.
(1) AC < AB
(2) BC < AB
A B
A B
如图(1),点C 落在线段AB的延长线(即以A为端点,方向为A到B的射线)上,设AB=a ,BC=b, 则线段AC就是线段a与线段b的和,记做AC = a + c ;
如图(2)线段AD就是线段a与线段b的差,记做AD =a- b.
像这样仅用圆规和没有刻度的直尺作图的方法叫尺规作图.
例1 如图,已知线段a,借助圆规和直尺作一条 线段使它等于2a.
作法:(1)作射线AD;(2)在AD上顺次截取AB=BC=a.则AC就是所要求作的线段.
1.如图,已知线段a,b.画一条线段,使它等于2a-b.
A B
作法略;如图所示,线段AD就是所求的线段.
A B
M N
在一张透明的纸上画一条线段,折叠纸片,使线段的端点重合,折痕与线段的交点就是线段的中点.动手试一试!
点M把线段AB分成相等的两条线段AM与MB,点M叫做线段AB的中点.
A B
类似地,还有线段的三等分点、四等分点等.
A B
M N P
2、 如图,线段AB=6cm,点C是AB的中点,点D是AC的中点,求线段AC,AD的长.
答:AC长为3cm,AD长为1.5cm.
1、已知线段AB = 4cm,延长AB到C,使BC = 2AB,若D为AB的中点,则线段DC 的长为 cm.
2cm + 8cm = 10cm
1.杭州湾跨海大桥是跨越杭州湾的便捷通道. 大桥北起嘉兴市,跨越宽阔的杭州湾海域后止于宁波市,全长36km. 大桥建成后宁波至上海间的陆路距离缩短了约120km. 你知道这是根据什么原理吗?
人们根据长期实践经验得到以下基本事实:
两点之间的所有连线中,线段最短.
简单说成:两点之间线段最短.
连接两点的线段的长度,叫做这两点间的距离.
如图:从A地到B地有四条道路,除它们外能否再修一条从A地到B地的最短道路?如果能,请你联系以前所学的知识,在图上画出最短路线.
解:如图所示,线段AB即为所求线段.
1.比较两条线段大小(长短)的方法:
A M B
因为点M是线段AB的中点,所以 AM=BM= AB(反过来说也是成立的).
4.两点之间线段最短.
5.连接两点的线段的长度,叫做这两点间的距离.
湘教版七年级上册4.2 线段、射线、直线教学ppt课件: 这是一份湘教版七年级上册4.2 线段、射线、直线教学ppt课件,文件包含教学课件七上·湘教·42线段射线直线第1课时线段射线直线pptx、42线段射线直线第1课时线段的比较与计算docx等2份课件配套教学资源,其中PPT共25页, 欢迎下载使用。
七年级上册4.2 直线、射线、线段优秀课件ppt: 这是一份七年级上册4.2 直线、射线、线段优秀课件ppt,共18页。PPT课件主要包含了学习目标,试一试,探究活动一,探究活动二,表示线段a,表示射线OA,表示直线l,议一议,有6条射线,探究活动三等内容,欢迎下载使用。
沪科版七年级上册4.2 线段、射线、直线教学课件ppt: 这是一份沪科版七年级上册4.2 线段、射线、直线教学课件ppt,共13页。PPT课件主要包含了创设情境引入新知,请你说一说,自主预习,自主探究,随堂练习,说一说你学到了什么,知识梳理等内容,欢迎下载使用。













