初中数学人教版八年级上册11.2.2 三角形的外角教案

11．2．2 三角形的外角

【教学目标】

1、知识与技能: 使学生初步掌握三角形内角和定理的两个推论，并会应用．。

2、过程与方法：培养学生总结知识内容，使之条理化，以便加深理解和记忆，养成良好的学习习惯．

3、情感态度与价值观：

⑴培养学生的推理能力，运用几何语言有条理的表达能力。

⑵通过师生共同活动，促进学生在学习活动中培养良好的情感，合作交流，主动参与的意识，在独立思考的同时能够认同他人。

【重点】三角形内角和定理推论的应用．

【难点】三角形外角的概念．真正理解推论，并能灵活运用．

【课型】   新授课

【学习方法】自学与小组合作学习相结合的方法

【学习过程】

一、目标导入

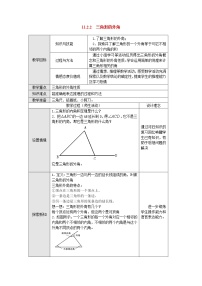
〔投影1〕如图，△ABC的三个内角是什么？它们有什么关系？

（是∠A、∠B、∠C，它们的和是1800。）

若延长BC至D，则∠ACD是什么角？这个角与△ABC的三个内角有什么关系？

二、自主学习(1)：

1.自学内容：教材第15页“思考”上.

2.自学要求：学生理解三角形外角的概念。

三、交流展示(1)：

1：三角形外角的定义：________________________________

2：外角的特征有三：(1)顶点在___________上．(2)一条边是______________．(3)另一条边是__________________．

3、画出一个三角形，并画出它的所有外角。

4、下列图中，∠1、∠2、∠3哪些是△ABC的外角？

四、自主学习(2)：

1.自学内容：课本15页思考到15页第3行；

2.自学要求：学生理解三角形内角和定理推论

五、交流展示(2)

容易知道，三角形的外角∠ACD与相邻的内角∠ACB是邻补角，那与另外两个角有怎样的数量关系呢？

〔投影2〕如图，这是我们证明三角形内角和定理时画的辅助线，你能就此图说明∠ACD与∠A、∠B的关系吗？

∵CE∥AB， ∴∠A=∠1，∠B=∠2

又∠ACD=∠1+∠2

∴∠ACD=∠A+∠B

你能用文字语言叙述这个结论吗？

三角形的一个外角等于与它不相邻的两个内角之和。

由加数与和的关系你还能知道什么？

三角形的一个外角大于与它不相邻的任何一个内角。

即  ，。

六、自主学习(3)：

1.自学内容：课本15页例题；

2.自学要求：学生能灵活运用三角形内角和定理推论

例  如图，∠1、∠2、∠3是三角形ABC的三个外角，它们的和是多少？

    分析：∠1与∠BAC、∠2与∠ABC、∠3与∠ACB有什么关系？∠BAC、ABC、∠ACB有什么关系？

解：∵∠1+∠BAC=1800，∠2+∠ABC=1800，∠3+∠ACB=1800，

∴∠1+∠BAC+∠2+∠ABC+∠3+∠ACB=5400

     又∠BAC+∠ABC+∠ACB=1800

∴∠1+∠2+∠3==3600。

你能用语言叙述本例的结论吗？

三角形外角的和等于3600。

七、交流展示(3)

1、课本15页练习

2、已知：D是AB上一点，E是AC上一点，BE、CD相交于F，∠A=62°，∠ACD=35°，∠ABE=20°

求：(1)∠BDC度数．(2)∠BFD度数．

八、巩固练习：

1. 一个三角形的两内角分别55°和65°，它的外角不可能是（    ）

A. 115°   B. 120°   C. 125°   D. 130°

2. 已知三角形的一个外角小于与它相邻的内角，那么这个三角形是（    ）

A. 锐角三角形 B. 直角三角形 C. 钝角三角形  D. 以上三种情况都有可能

3. 已知，如图，在△ABC中，D是三角形内一点，

求证：∠BDC>∠BAC。

九、小结

1、什么是三角形外角？

2、三角形的外角有哪些性质？

（1. 三角形的外角与它相邻的内角互补。

2. 三角形的一个外角等于和它不相邻的两个内角的和。

3. 三角形的一个外角大于任何一个和它不相邻的内角。

4. 三角形的外角和等于360°。

找三角形的外角是难点，特别是当一个角是某个三角形的内角，同时又是另一个三角形的外角时，困难就更大，解决这个难点的方法是讲清定义，图形分析，变换位置，思路清晰．）

十、布置作业：课本16页2、5、6、8、10。