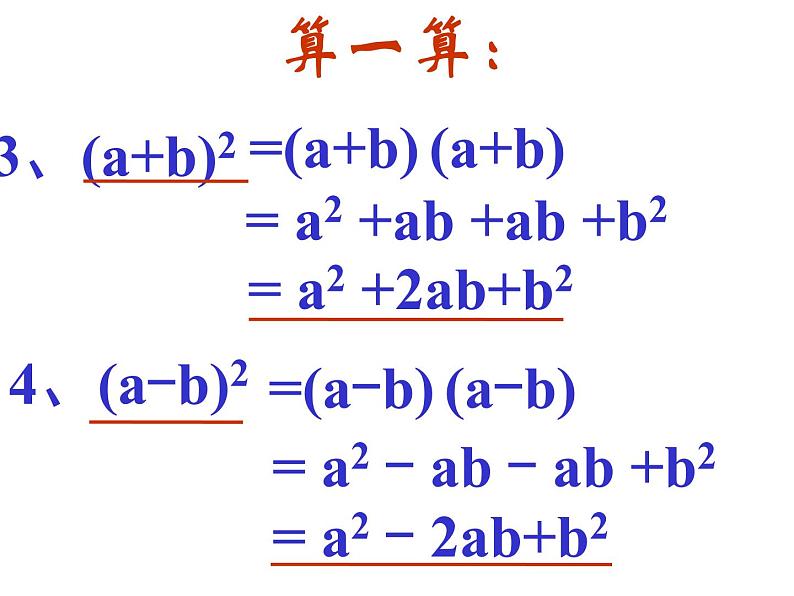
苏科版七年级下册第9章 整式乘法与因式分解9.4 乘法公式课文配套ppt课件

这是一份苏科版七年级下册第9章 整式乘法与因式分解9.4 乘法公式课文配套ppt课件，共27页。PPT课件主要包含了算一算，a+b2，a-b2，你会了吗，课堂检测等内容，欢迎下载使用。

复习提问：
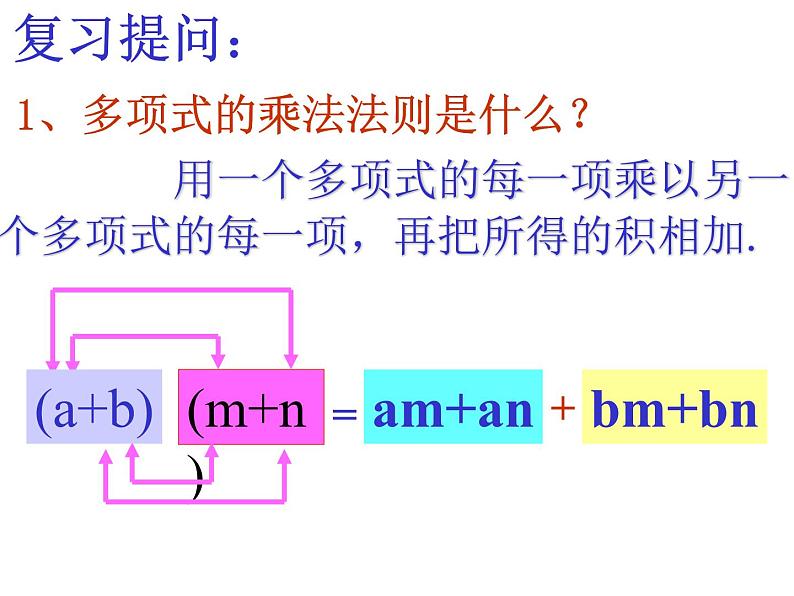
用一个多项式的每一项乘以另一个多项式的每一项，再把所得的积相加.
1、多项式的乘法法则是什么？
1、(a+1)(a+1)
2、(mn+a)(mn+a)
= a2 +2ab+b2
= a2 - 2ab+b2
= a2 +ab +ab +b2
= a2 - ab - ab +b2
=(a+b) (a+b)
=(a-b) (a-b)
完全平方公式的数学表达式：
完全平方公式的文字叙述：
两个数的和（或差）的平方，等于它们的平方和，加上（或减去）它们的积的2倍。
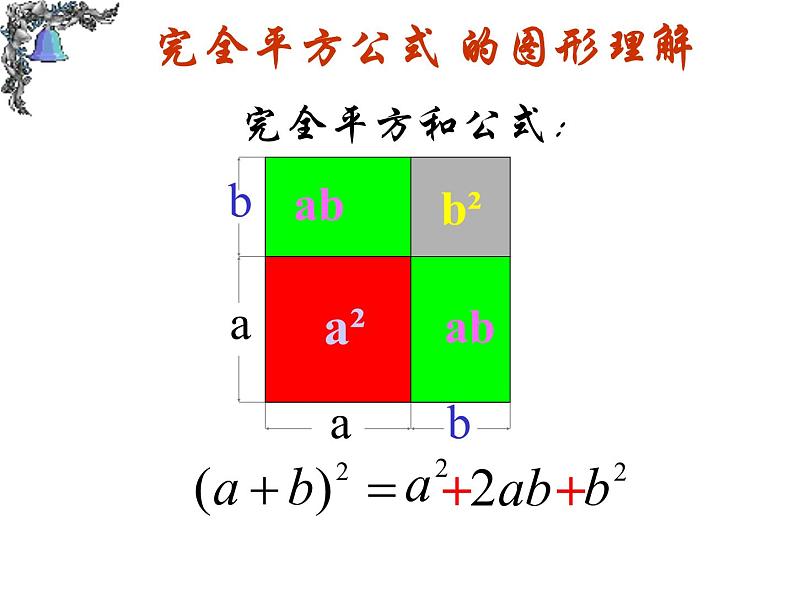
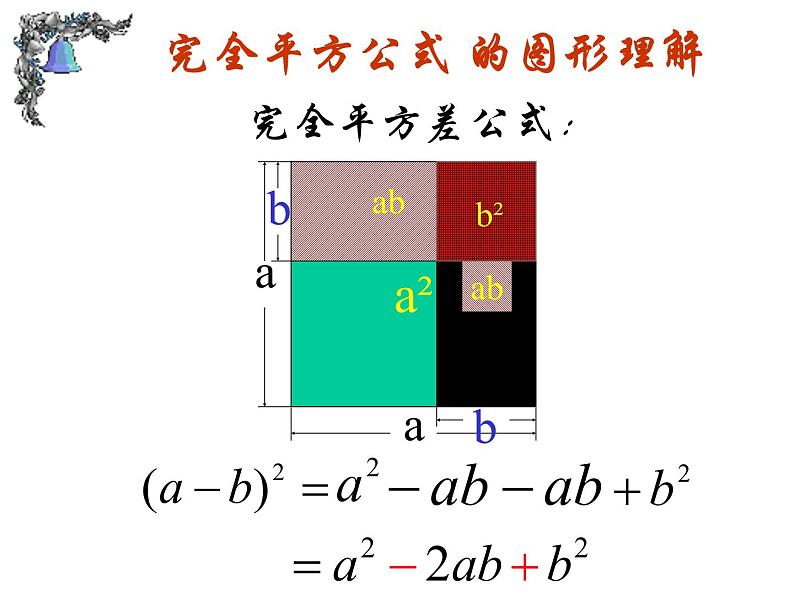
完全平方公式 的图形理解
4、公式中的字母a，b可以表示数，单项式和 多项式。
(a+b)2= a2 +2ab+b2(a-b)2= a2 - 2ab+b2
2、积中两项为两数的平方和；
3、另一项是两数积的2倍，且与乘式中 间的符号相同。
首平方，尾平方，首尾两倍中间放
下面各式的计算是否正确？如果不正确，应当怎样改正？
(x+y)2=x2 +y2
(2)(x -y)2 =x2 -y2
(3) (x -y)2 =x2+2xy +y2
(4) (x+y)2 =x2 +xy +y2
(x +y)2 =x2+2xy +y2
(x -y)2 =x2 -2xy +y2
例1 运用完全平方公式计算：
解： (x+2y)2=
(a +b)2= a2 + 2 ab + b2
解： (x-2y)2=
(a - b)2= a2 - 2 ab + b2
（1）(2x+y)2 = （2）(4-y)2 =（3）(2m-n)2=
例2、运用完全平方公式计算：
(1) ( 4m2 - n2 )2
（ 4m2 － n2）2
=( )2－2( )·( )+( )2
=16m4－8m2n2+n4
记清公式、代准数式、准确计算。
(a-b)2= a2 - 2ab+b2
1.(3x2-7y)2=
2.(2a2+3b3)2=
在解题过程中要准确确定a和b、对照公式原形的两边, 做到(1)不丢项(2)不弄错符号(3)2ab时不少乘2；(4)两数是乘积形式时，被平方时要注意添括号
填空(1)(a+ )2=a2+4ab+4b2(2) (2a+ )2=4a2+4ab+b2(3) (3x－ )2=9x2－12xy2+( ) (4)( －x－ )2=x2+ +1
如何计算 (a+b+c)2
解: (a+b+c)2 =[(a+b)+c]2 =(a+b)2+2·(a+b)·c+c2 =a2+2ab+b2+2ac+2bc+c2 =a2+b2+c2+2ab+2ac+2bc
例3、运用完全平方公式进行简便计算：
=10000+800+16
= (100 –0. 1)2
=10000 -20+0.01
练习：利用完全平方公式计算：
(-a+b)2 =(b-a)2 =(a-b)2
(-a-b)2 =(a+b)2
1.(-x-y)2=
2.(-2a2+b)2=
小兵计算一个二项整式的平方式时得到正确结果是4x2+ +25y2,但中间一项不慎被污染了,这一项应是( )A 10xy B 20xy C±10xy D±20xy
(1) (6a+5b)2 =36a2+60ab+25b2
(2) (4x-3y)2 =16x2-24xy+9y2
(4) (2m-1)2 =4m2-4m+1
(3) (-2m-1)2 =4m2+4m+1
（1）(6a+5b)2 (3)(-2m-1)2（2）(4x-3y)2 (4)(2m-1)2
本节课你的收获是什么？
有时需要进行变形，使变形后的式子符合应用完全平方公式的条件，即为“两数和(或差)的平方”，然后应用公式计算.
在解题过程中要准确确定a和b、对照公式原形的两边, 做到不丢项、不弄错符号、2ab时不少乘2；第一(二)数是乘积被平方时要注意添括号, 是运用完全平方公式进行多项式乘法的关键