初一数学2022年宜兴市外国语学校3月月考试题

这是一份初一数学2022年宜兴市外国语学校3月月考试题，文件包含第一次练习doc、数学练习1答卷doc等2份试卷配套教学资源，其中试卷共9页， 欢迎下载使用。

（本卷满分150分，测试时间120分钟）
一、选择题（每小题3分，共30分.把正确的答案前的字母填入下表相应的括号）
1. 同桌读了：“子非鱼焉知鱼之乐乎？”后，兴高采烈地利用电脑画出了左图鱼的图案，请问：由图中所示的图案通过平移后得到的图案是（ ）
A. B. C. D.
2．下列运算正确的是 （ ）
A． B． C． D．
3．下列长度的三根木棒首尾相接，不能做成三角形框架的是（ ）
A．5cm、7cm、2cm B．7cm、13cm、10cmC．5cm、7cm、11cm D．5cm、10cm、13cm
4．已知a＝96，b＝314，c＝275，则a、b、c的大小关系是（ ）
a
b
1
3
2
4
5
（第6题）
A．a＞b＞cB．a＞c＞bC．c＞b＞aD．b＞c＞a
5．下列说法正确的是（ ）
A．三角形的三条高至少有一条在三角形内
B．直角三角形只有一条高
C．三角形的角平分线其实就是角的平分线
D．三角形的角平分线、中线、高都在三角形的内部
6.如图，下列条件中，能判断直线a∥b的是 （ ）
A．∠2=∠3 B．∠1=∠3 C．∠4＋∠5=180° D．∠2=∠4
7．多边形剪去一角后，多边形的外角和将 ( )
A．减少180° B．不变 C．增大180° D．以上都有可能
8、如图，把一块含45°角的三角板的直角顶点靠在长尺（两边a∥b）的一边b上，若∠1=30°，则三角板的斜边所在直线与长尺的另一边a的夹角∠2的度数为（ ）
A．10° B．15° C．30° D．35°
9. 如图，△ABC的角平分线 CD、BE相交于F，∠A＝90°，
EG∥BC，且CG⊥EG于G，下列结论：①∠CEG＝2∠DCB；
②CA平分∠BCG；③∠ADC＝∠GCD；④∠DFB＝ eq \f(1,2)∠CGE．
其中正确的结论是………………………………………( )
A．①③ B．②④ C．①③④ D．①②③④
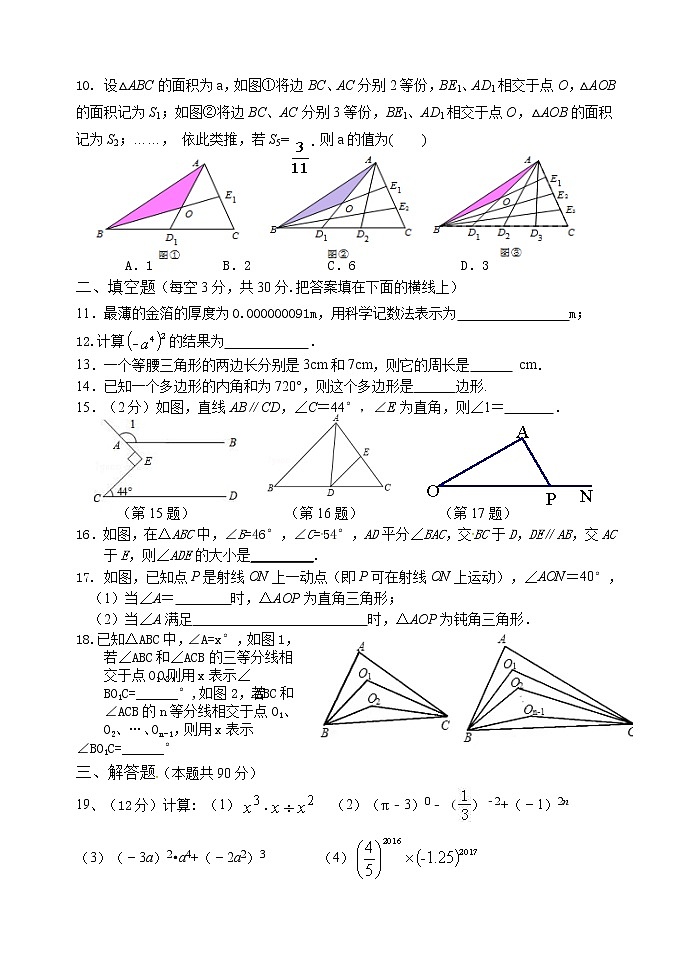
10. 设△ABC的面积为a，如图①将边BC、AC分别2等份，BE1、AD1相交于点O，△AOB的面积记为S1；如图②将边BC、AC分别3等份，BE1、AD1相交于点O，△AOB的面积记为S2；……， 依此类推，若S5=，则a的值为( )
A．1 B．2 C．6 D．3
二、填空题（每空3分，共30分.把答案填在下面的横线上）
11．最薄的金箔的厚度为0.000000091m，用科学记数法表示为 m；
12.计算的结果为 ．
13．一个等腰三角形的两边长分别是3cm和7cm，则它的周长是 cm．
14．已知一个多边形的内角和为720°，则这个多边形是 边形.[来源:学*
15．（2分）如图，直线AB∥CD，∠C＝44°，∠E为直角，则∠1＝ ．
（第15题） （第16题） （第17题）
16．如图，在△ABC中，∠B=46°，∠C=54°，AD平分∠BAC，交BC于D，DE∥AB，交AC于E，则∠ADE的大小是_________.
17. 如图，已知点P是射线ON上一动点（即P可在射线ON上运动），∠AON＝40°，
（1）当∠A＝ 时，△AOP为直角三角形；
（2）当∠A满足 时，△AOP为钝角三角形．
18.已知△ABC中，∠A=x°，如图1，若∠ABC和∠ACB的三等分线相交于点O1、O2，则用x表示∠BO1C=______°,如图2，若∠ABC和∠ACB的n等分线相交于点O1、O2、…、On-1，则用x表示
∠BO1C=______°
SHAPE \* MERGEFORMAT 三、解答题（本题共90分）
19、（12分）计算: （1） （2）（π﹣3）0﹣（）﹣2+（﹣1）2n
（3）（﹣3a）2•a4+（﹣2a2）3 （4）
20．(4分)先化简再求值 - (-2)·(-) + (-)，其中= -，=2．
21（8分）（1）已知,求的值.
（2）已知，求x的值.
22．（8分）如图，在边长为1个单位的正方形网格中，△ABC经过平移后得到△A′B′C′，图中标出了点B的对应点B′．根据下列条件，利用网格点和无刻度的直尺画图并解答相关的问题（保留画图痕迹）：
（1）画出△A′B′C′；（2）画出△ABC的高BD；
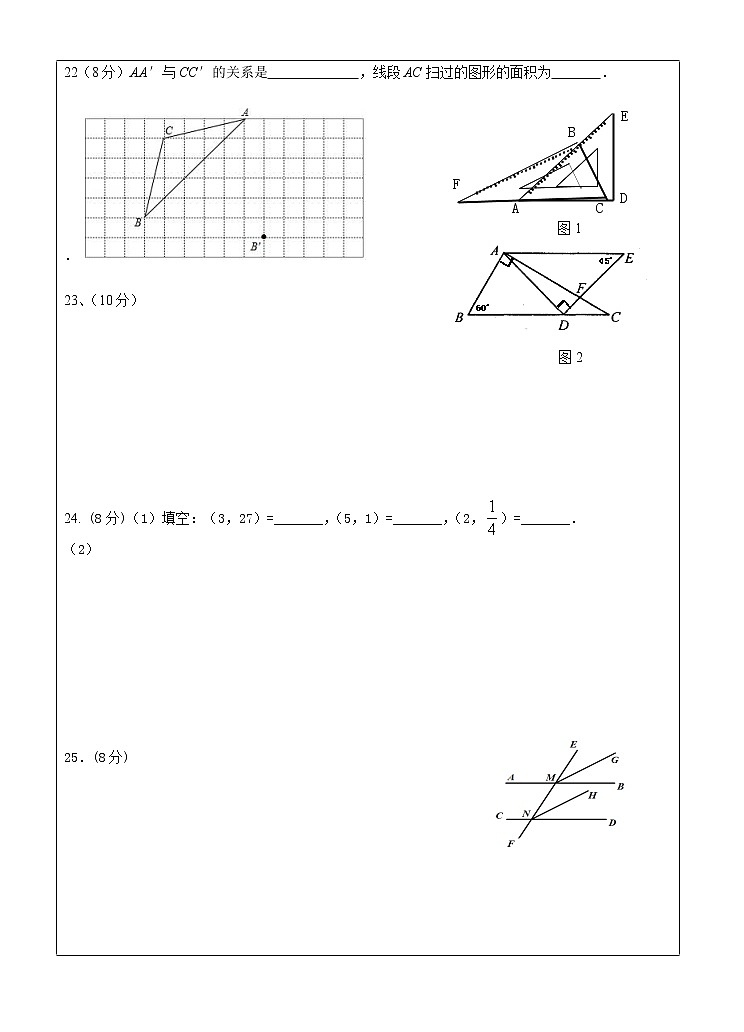
（3）连接AA′、CC′，那么AA′与CC′的关系是 ，线段AC扫过的图形的面积为 ．
A
B
C
D
E
F
23、（10分）生活中到处都存在着数学知识，只要同学们学会用数学的眼光观察生活，就会有许多意想不到的收获，下面两幅图都是由同一副三角板拼凑得到的：
图2
图1
（1）请你计算出图1中的∠ABC的度数.
（2）图2中AE∥BC，请你计算出∠AFD的度数．
24. (8分)规定两数，b之间的一种运算，记作(，b)：如果， QUOTE 那么(，b)=c．
例如：因为23=8，所以(2，8)=3．
（1）根据上述规定，填空：（3，27）=_______，（5，1）=_______，（2， QUOTE ）=_______．
（2）小明在研究这种运算时发现一个现象：（3n，4n）=（3，4）小明给出了如下的证明：
设（3n，4n）=，则（3n）x=4n，即（3x）n=4n 所以3x=4，即（3，4）=，
所以（3n，4n）=（3，4）．
请你尝试运用这种方法证明下面这个等式：(3，4)+(3，5)=(3，20)
25．(8分)如图，直线EF分别与直线AB、CD交于点M、N，
MG平分∠EMB，NH平分∠END，且MG//NH.求证：AB//CD.
C
B
D
E
F
A
26．（10分）在△ABC中，AE⊥BC于点E，∠BAE∶∠CAE＝4∶6，BD平分∠ABC，点F在BC上，∠CDF＝60°，∠ABD＝25°．
（1）求∠CAE的度数；
（2）求证：DF⊥BC．
27、 (10分)初一（1）班数学学习小组在学习了第七章平面图形的认识（二）后对几何学习产生了浓厚的兴趣．请你认真研读下列三个片断，并完成相关问题．如图1，直线OM⊥ON，垂足为O，三角板的直角顶点C落在∠MON的内部，三角板的另两条直角边分别与ON、OM交于点D和点B．
【片断一】小孙说：由四边形内角和知识很容易得到∠OBC+∠ODC的值．如果你是小孙，得到的正确答案应是：∠OBC+∠ODC = °．
【片断二】小康说：连结BD（如图2），若BD平分∠OBC，那么BD也平分∠ODC．请你说明当BD平分∠OBC时，BD也平分∠ODC的理由．
【片断三】小雪说：若DE平分∠ODC、BF平分∠MBC，我发现DE与BF具有特殊的位置关系．请你先在备用图中补全图形，再判断DE与BF有怎样的位置关系并说明理由．
28. (12分) 已知△ABC中，∠ABC=∠ACB，D为射线CB上一点（不与C、B重合），点E为射线CA上一点，∠ADE=∠AED．设∠BAD=α，∠CDE=β．
（1）如图（1），①若∠BAC=40°，∠DAE=30°，则α= ，β= ．
②写出α与β的数量关系，并说明理由；（2）如图（2），当D点在BC边上，E点在CA的延长线上时，其它条件不变，写出α与β的数量关系，并说明理由．（3）如图（3），D在CB的延长线上，根据已知补全图形，并直接写出α与β的关系式 ．