初三数学2022年宜兴市外国语学校初三数学3月月考试题

这是一份初三数学2022年宜兴市外国语学校初三数学3月月考试题，文件包含试卷-初三数学20223docx、答卷-初三数学20223doc等2份试卷配套教学资源，其中试卷共11页， 欢迎下载使用。

出卷： 张洪娟 审核：初三数学备课组 （ 2022 年3月）
一、选择题：（本大题共10小题，每小题3分，共30分．）
1．|﹣9|的值是( ▲ )
A．9 B．﹣9 C． D．±9
2．据报道，首张黑洞照片于北京时间2019年4月10日在全球六地同步发布，该黑洞位于处女座一个巨椭圆星系M87的中心，距离地球5500万光年．其中5500万用科学记数法表示为( ▲ )
A．55×106B．5.5×106C．5.5×107D．5.5×108
3．下列调查方式中合适的是( ▲ )
A.要了解一批节能灯的使用寿命，采用普查方式
B.调查你所在班级同学的身高，采用抽样调查方式
C.环保部门调查太湖某段水域的水质情况，采用抽样调查方式
D.调查全市初三学生每天的就寝时间，采用普查方式
4.一几何体的三视图如图所示，这个几何体是( ▲ )
A．四棱锥 B．圆锥 C．三棱柱 D．四棱柱
5．下列说法不一定成立的是( ▲ )
A．若a>b，则a+c>b+cB．若a+c>b+c，则a>b
C．若a>b，则ac2>bc2D．若a>b，则1+a>b-1
6. 在音乐比赛中，常采用“打分类制”，经常采用这样的办法来得到一名选手的最后成绩：将所有评委的打分组成一组数据，去掉一个最高分和一个最低分，得到一组新的数据，再计算平均分．假设评委不少于10人，则比较两组数据，一定不会发生变化的是（ ▲ ）
A．平均数B．中位数C．众数D．方差
7．如图，在的网格中，A，B均为格点，以点A为圆心，以AB的长为半径作弧，图中的点C是该弧与格线的交点，则的值是（ ▲ ）
A． B． C． D．
8．如图，△AOB和△ACD均为正三角形，且顶点B、D均在双曲线上，若图中S△OBP＝4，则k的值为（ ▲ ）
A．B．
C．﹣4D．4
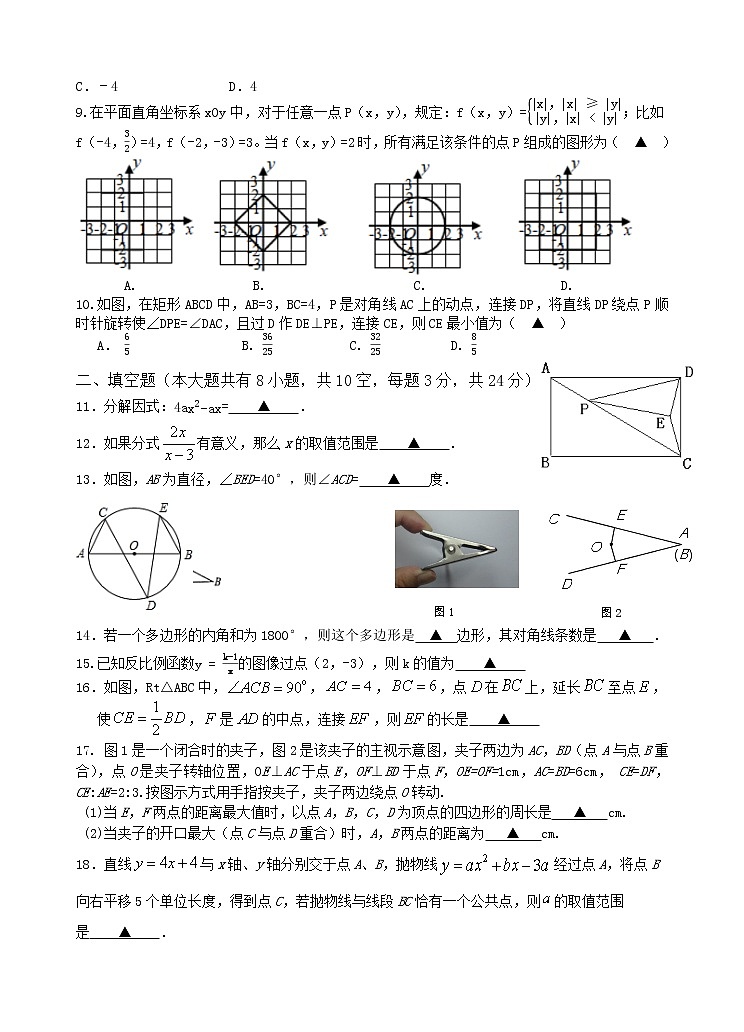
9.在平面直角坐标系xOy中，对于任意一点P（x，y），规定：f（x，y）=x，x≥yy，xf（-4，32）=4，f（-2，-3）=3。当f（x，y）=2时，所有满足该条件的点P组成的图形为（ ▲ ）

B. C. D.
10.如图，在矩形ABCD中，AB=3，BC=4，P是对角线AC上的动点，连接DP，将直线DP绕点P顺时针旋转使∠DPE=∠DAC，且过D作DE⊥PE，连接CE，则CE最小值为（ ▲ ）
A． 65 B. 3625 C. 3225 D. 85
二、填空题（本大题共有8小题，共10空，每题3分，共24分）
11．分解因式：4ax2−ax= ▲ ．
12．如果分式有意义，那么x的取值范围是 ▲ ．
C
E
(B)
A
O
F
D
图1
图2
13．如图，AB为直径，∠BED=40°，则∠ACD= ▲ 度．
14．若一个多边形的内角和为1800°，则这个多边形是 ▲ 边形，其对角线条数是 ▲ ．
15.已知反比例函数y=k−1x的图像过点（2，-3），则k的值为 ▲
16．如图，Rt△ABC中，，，，点在上，延长至点，使，是的中点，连接，则的长是 ▲
17. 图1是一个闭合时的夹子，图2是该夹子的主视示意图，夹子两边为AC，BD（点A与点B重合），点O是夹子转轴位置，OE⊥AC于点E，OF⊥BD于点F，OE=OF=1cm，AC=BD=6cm， CE=DF， CE:AE=2:3.按图示方式用手指按夹子，夹子两边绕点O转动.
(1)当E，F两点的距离最大值时，以点A，B，C，D为顶点的四边形的周长是 ▲ cm.
(2)当夹子的开口最大（点C与点D重合）时，A，B两点的距离为 ▲ cm.
18．直线与x轴、y轴分别交于点A、B，抛物线经过点A，将点B向右平移5个单位长度，得到点C，若抛物线与线段BC恰有一个公共点，则的取值范围
是 ▲ ．
三、解答题（本大题共有10小题，共96分）
19．（本题满分8分）
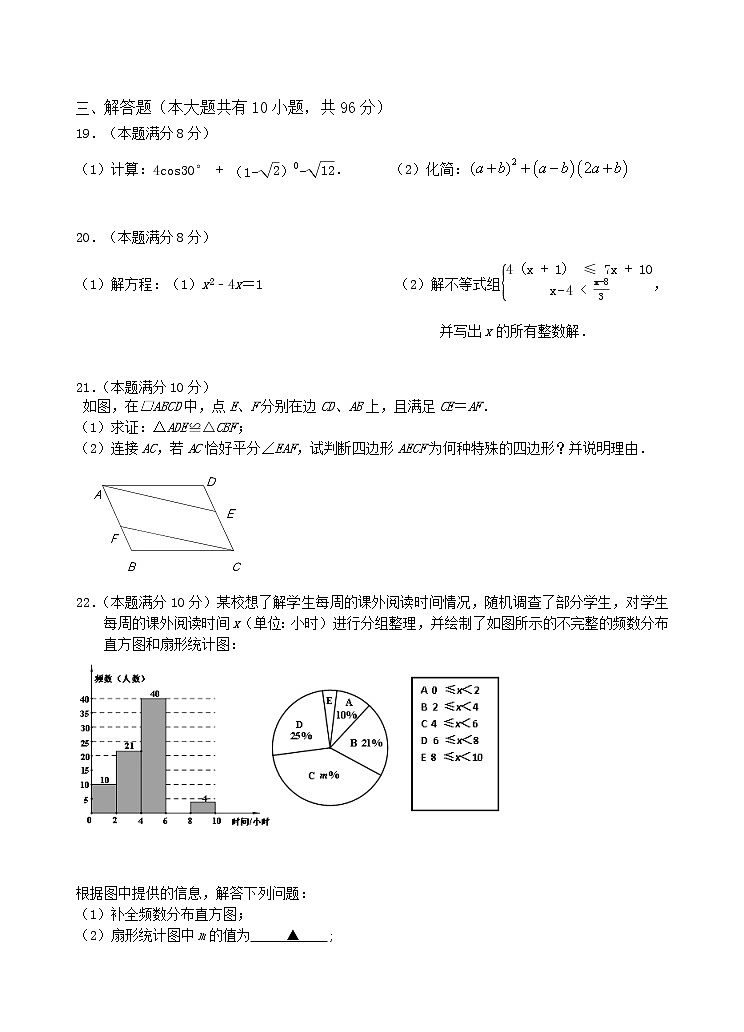
（1）计算：4cs30°+（1−2）0−12． （2）化简：
20．（本题满分8分）
（1）解方程：（1）x2﹣4x＝1 （2）解不等式组4x+1≤7x+10x−4并写出x的所有整数解．
21．（本题满分10分）
如图，在□ABCD中，点E、F分别在边CD、AB上，且满足CE＝AF．
（1）求证：△ADE≌△CBF；
（2）连接AC，若AC恰好平分∠EAF，试判断四边形AECF为何种特殊的四边形？并说明理由．
D
E
F
A
B
C
22．（本题满分10分）某校想了解学生每周的课外阅读时间情况，随机调查了部分学生，对学生每周的课外阅读时间x（单位：小时）进行分组整理，并绘制了如图所示的不完整的频数分布直方图和扇形统计图：
根据图中提供的信息，解答下列问题：
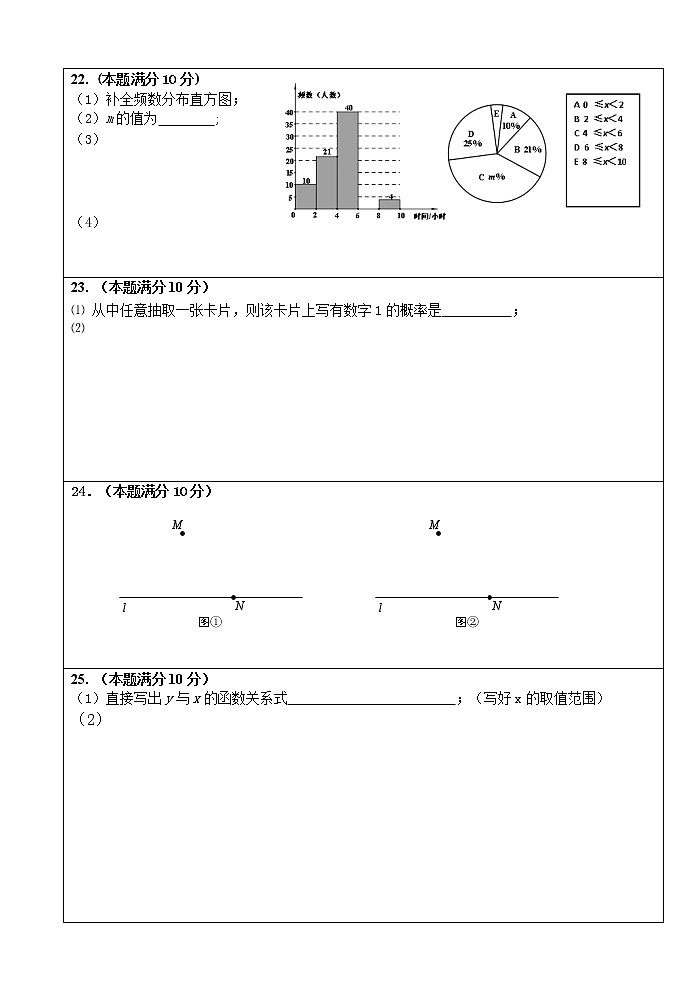
（1）补全频数分布直方图；
（2）扇形统计图中m的值为 ▲ ;
（3）求E组对应的圆心角度数；
（4）请估计该校3000名学生中每周的课外阅读时间不小于6小时的人数．
23.（本题满分10分）在一个不透明的盒子中放有四张分别写有数字1、2、3、4的红色卡片和三张分别写有数字1、2、3的蓝色卡片，卡片除颜色和数字外其它完全相同．
⑴ 从中任意抽取一张卡片，则该卡片上写有数字1的概率是 ▲ ；
⑵ 将3张蓝色卡片取出后放入另外一个不透明的盒子内，然后在两个盒子内各任意抽取一张卡片，以红色卡片上的数字作为十位数，蓝色卡片上的数字作为个位数组成一个两位数，求这个两位数大于22的概率．（请利用树状图或列表法说明）
24.（本题满分10分）
如图，已知点M在直线l外，点N在直线l上，请用无刻度的直尺和圆规完成下列作图，要求保留作图痕迹，不写作法．
（1）在图①中，以线段MN为一条对角线作菱形MPNQ，使菱形的边PN落在直线l上；
（2）在图②中，作⊙O，使⊙O过点M，且与直线l相切于点N．
图①
M
N
l
图②
M
N
l
复制发布25.（本题满分10分）某企业接到一批防护服生产任务，按要求15天完成，已知这批防护服的出厂价为每件80元，为按时完成任务，该企业动员放假回家的工人及时返回加班赶制．该企业第x天生产的防护服数量为y件，y与x之间的关系可以用图中的函数图象来刻画．
（1）直接写出y与x的函数关系式 ▲ ；（写好x的取值范围）
（2）由于特殊原因，原材料紧缺，服装的成本前5天为每件50元，从第6天起每件服装的成本比前一天增加2元，设第x天创造的利润为w元，直接利用（1）的结论，求w与x之间的函数表达式，并求出第几天的利润最大，最大利润是多少元？（利润＝出厂价﹣成本）
26. （本题满分10分）如图，在菱形ABCD中，已知∠BAD＝120°，对角线BD长为12．
（1）求菱形ABCD的周长；
（2）动点P从点A出发，沿A→B的方向，以每秒1个单位的速度向点B运动；在点P出发的同时，动点Q从点D出发，沿D→C→B的方向，以每秒2个单位的速度向点B运动．设运动时间为t（s）．
（备用图）

①当PQ恰好被BD平分时，试求t的值；
②连接AQ，直接写出：在整个运动过程中，当t取怎样的值时，△APQ恰好是一个直角三角形？
27．（本题满分10分）阅读理解：我们知道，四边形具有不稳定性，容易变形. 如图1，一个矩形发生变形后成为一个平行四边形. 设这个平行四边形相邻两个内角中较小的一个内角为，我们把的值叫做这个平行四边形的变形度.
(1) 若矩形发生变形后的平行四边形有一个内角是150°，则这个平行四边形的变形度是_ ▲ _．；
猜想证明：（2）若矩形的面积为，其变形后的平行四边形面积为，试猜想，，之间的数量关系，并说明理由；
拓展探究：（3）如图2，在矩形中，是边上的一点，且，这个矩形发生变形后为平行四边形，为的对应点，连接，，若矩形的面积为，平行四边形的面积为，试求的度数.

28.（本题满分10分）
如图，抛物线y＝x2＋bx＋c的顶点为M，对称轴是直线x＝1，与x轴的交点为A(－3，0)和B．将抛物线y＝x2＋bx＋c绕点B逆时针方向旋转90°，点M1，A1为点M，A旋转后的对应点，旋转后的抛物线与y轴相交于C，D两点．
(1)写出点B的坐标及求原抛物线的解析式：
(2)求证A，M，A1三点在同一直线上：
(3)设点P是旋转后抛物线上DM1之间的一动点，是否存在一点P，使四边形PM1MD的面积最大．如果存在，请求出点P的坐标及四边形PM1MD的面积；如果不存在，请说明理由．
图1