初一数学2022年江阴市敔山湾学校3月月考试题

这是一份初一数学2022年江阴市敔山湾学校3月月考试题，文件包含敔山湾实验学校20212022学年度第二学期3月作业检查七创年级数学参考答案doc、敔山湾实验学校20212022学年度第二学期3月作业检查七创年级数学试卷doc、敔山湾实验学校20212022学年度第二学期3月作业检查七创年级数学试卷pdf、202203敔山湾普通班初一数学doc、敔山湾实验学校20212022学年度第二学期3月作业检查七创年级数学答卷-答题卡pdf等5份试卷配套教学资源，其中试卷共30页， 欢迎下载使用。

命题人：缪路 审题人：胡欣怡
满分120分 考试时间为100分钟
一、选择题（本大题共有10小题，每小题3分，共30分，在每小题所给出的四个选项中，只有一项是正确的，请把正确选项前的字母代号填在题后的括号内）
1．如图，线段AB＝DE，点C为线段AE的中点，下列式子不正确的是 （ ）
A．BC＝CDB．CD＝EQ \F(1,2)AE﹣ABC．CD＝AD﹣CED．CD＝DE

第1题 第2题 第5题 第6题
2．如图，∠MON为锐角．下列说法：①∠MOP＝eq \s\d2(\f(1,2))∠MON；②∠MOP＝∠NOP＝eq \s\d2(\f(1,2))∠MON；③∠MOP＝∠NOP；④∠MON＝∠MOP+∠NOP．其中，能说明射线OP一定为∠MON的平分线的有 （ ）
A．1个B．2个C．3个D．4个
3．下列说法：①两点之间的所有连线中，线段最短；②相等的角是对顶角； ③过一点有且仅有一条直线与已知直线平行； ④两点之间的距离是两点间的线段； ⑤若AB＝BC，则点B为线段AC的中点；⑥不相交的两条直线叫做平行线．其中正确的个数是 （ ）
A．0个B．1个C．2个D．3个
4．若B地在A地的南偏东53°的方向上，则A地在B地的方位是 （ ）
A．北偏西53°B．北偏西37°C．南偏东53°D．南偏东37°
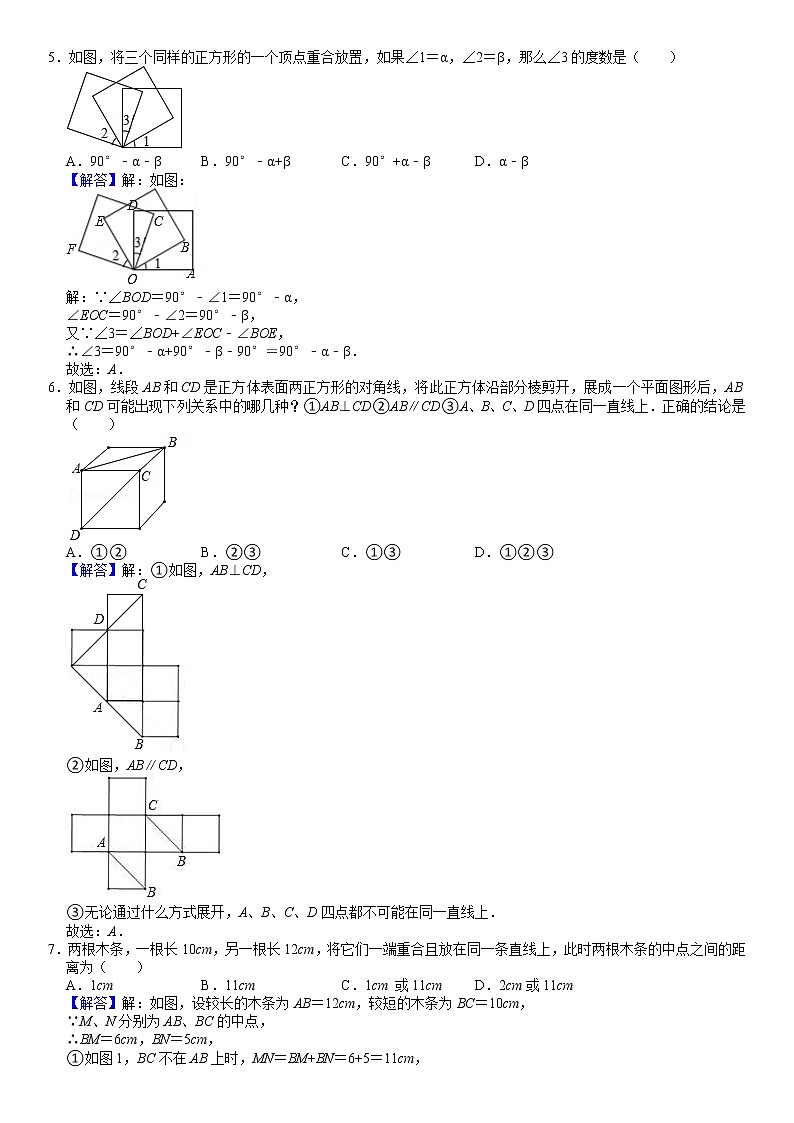
5．如图，将三个同样的正方形的一个顶点重合放置，如果∠1＝α，∠2＝β，那么∠3的度数是 （ ）
A．90°﹣α﹣βB．90°﹣α+βC．90°+α﹣βD．α﹣β
6．如图，线段AB和CD是正方体表面两正方形的对角线，将此正方体沿部分棱剪开，展成一个平面图形后，AB和CD可能出现下列关系中的哪几种？①AB⊥CD②AB∥CD③A、B、C、D四点在同一直线上．正确的结论是 （ ）
A．①②B．②③C．①③D．①②③
7．两根木条，一根长10cm，另一根长12cm，将它们一端重合且放在同一条直线上，此时两根木条的中点之间的距离为 （ ）
A．1cmB．11cmC．1cm 或11cmD．2cm或11cm
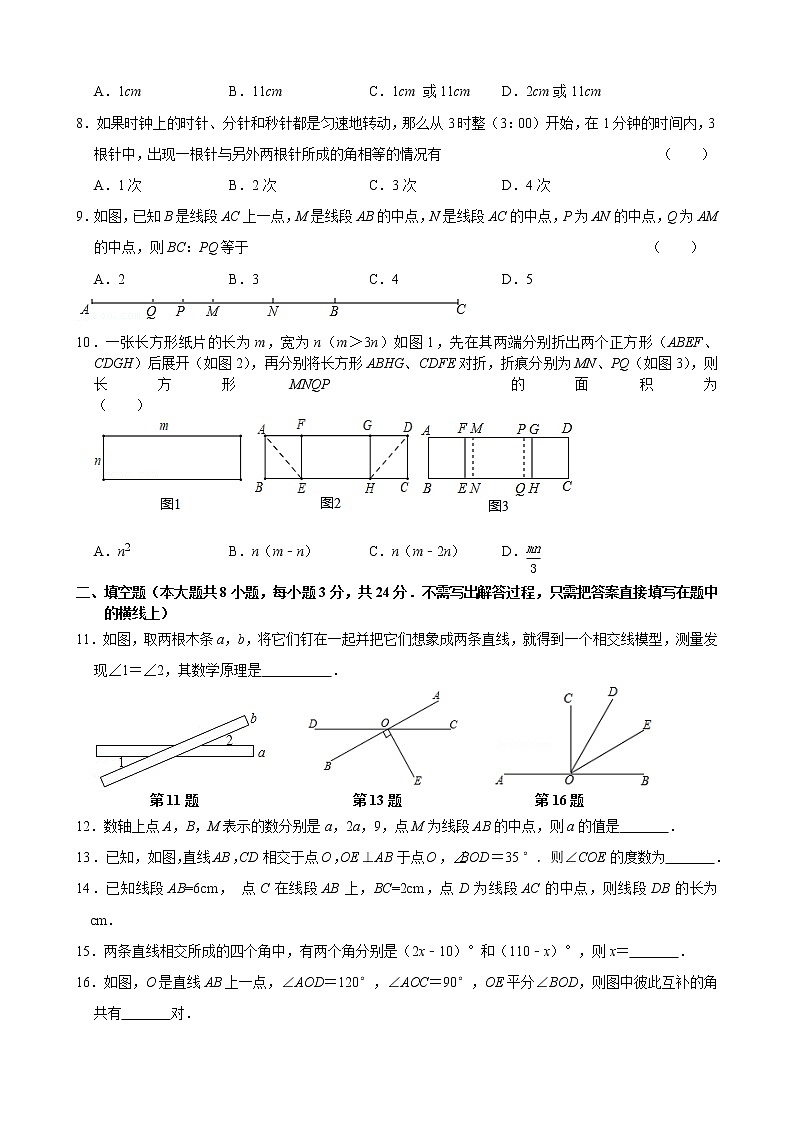
8．如果时钟上的时针、分针和秒针都是匀速地转动，那么从3时整（3：00）开始，在1分钟的时间内，3根针中，出现一根针与另外两根针所成的角相等的情况有 （ ）
A．1次B．2次C．3次D．4次
9．如图，已知B是线段AC上一点，M是线段AB的中点，N是线段AC的中点，P为AN的中点，Q为AM的中点，则BC：PQ等于 （ ）
A．2B．3C．4D．5
10．一张长方形纸片的长为m，宽为n（m＞3n）如图1，先在其两端分别折出两个正方形（ABEF、CDGH）后展开（如图2），再分别将长方形ABHG、CDFE对折，折痕分别为MN、PQ（如图3），则长方形MNQP的面积为 （ ）
A．n2B．n（m﹣n）C．n（m﹣2n）D．eq \s\d2(\f(mn,3))
二、填空题（本大题共8小题，每小题3分，共24分．不需写出解答过程，只需把答案直接填写在题中的横线上）
11．如图，取两根木条a，b，将它们钉在一起并把它们想象成两条直线，就得到一个相交线模型，测量发现∠1＝∠2，其数学原理是 ．

第11题 第13题 第16题
12．数轴上点A，B，M表示的数分别是a，2a，9，点M为线段AB的中点，则a的值是 ．
13．已知，如图，直线AB，CD相交于点O，OE⊥AB于点O，∠BOD＝35°．则∠COE的度数为 ．
14．已知线段AB=6cm， 点C在线段AB上，BC=2cm，点D为线段AC的中点，则线段DB的长为 cm．
15．两条直线相交所成的四个角中，有两个角分别是（2x﹣10）°和（110﹣x）°，则x＝ ．
16．如图，O是直线AB上一点，∠AOD＝120°，∠AOC＝90°，OE平分∠BOD，则图中彼此互补的角共有 对．
17．如图，已知线段AB长度为16，线段CD长度为3，线段CD在线段AB上自由运动（点C与A点不重合，D与B点不重合），若点E为AC的中点．则2BE﹣BD的值为 ．
18．如图，点P1是线段AB上一点，AP1＝2BP1，点P2是线段P1B上一点，P1P2＝2BP2；点P3是线段P2B上一点，P2P3＝2BP3，…，请借助所给的图形，计算（+++…+）的结果为 （n为正整数，用含n的代数式表示）
三、解答题（本大题共有8小题，共66分，解答时应写出文字说明，推理过程或演算步骤）
19．（9分）计算：
（1）45°10′﹣21°35′20′′ （2）48°39′+67°31′﹣21°17′； （3）42°16′+18°23′×2．
20．（6分）已知一个角的余角比这个角的补角的eq \s\d2(\f(1,4))小12°，求这个角的度数．
21．（8分）如图，在6×6的正方形网格中，每个小正方形的边长是1，点M、N、P、Q均为格点（格点是指每个小正方形的顶点），线段MN经过点P．
（1）过点P画线段AB，使得线段AB满足以下两个条件：①AB⊥MN；②AB＝MN；
（2）过点Q画MN的平行线CD，CD与AB相交于点E；
（3）若格点F使得△PFM的面积等于4，则这样的点F共有 个．
22．（8分）如图，O为直线AB上一点，OC为射线，OD、OE分别为∠AOC、∠BOC的平分线．
（1）判断射线OD、OE的位置关系，并说明理由；
（2）若∠AOD＝30°，求证：OC为∠AOE的平分线；
（3）如果∠AOD：∠AOE＝2：11，求∠BOE的度数．
23．（6分）直线l上的三个点A、B、C，若满足BC＝eq \s\d2(\f(1,2))AB，则称点C是点A关于点B的“半距点”．如图1，BC＝eq \s\d2(\f(1,2))AB，此时点C就是点A关于点B的一个“半距点”．
若M、N、P三个点在同一条直线m上，且点P是点M关于点N的“半距点”，MN＝6cm．
（1）MP＝ cm；
（2）若点G也是直线m上一点，且点G是线段MP的中点，求线段GN的长度．
24．（8分）A，B，C，D是长方形纸片的四个顶点，点E、F、H分别是边AB、BC、AD上的三点，连接EF、FH．
（1）将长方形纸片ABCD按图①所示的方式折叠，FE、FH为折痕，点B、C、D折叠后的对应点分别为B'、C'、D'，点B'在FC'上，则∠EFH的度数为 ；
（2）将长方形纸片ABCD按图②所示的方式折叠，FE、FH为折痕，点B、C、D折叠后的对应点分别为B'、C'、D'，若∠B'FC'＝18°，求∠EFH的度数；
（3）将长方形纸片ABCD按图③所示的方式折叠，FE、FH为折痕，点B、C、D折叠后的对应点分别为B'、C'、D'，若∠EFH＝m°，则∠B'FC'的度数为 ．
25．（10分）如图，数轴上A，B两点对应的有理数分别为﹣10和20，点P从点O出发，以每秒1个单位长度的速度沿数轴正方向匀速运动，点Q同时从点A出发，以每秒2个单位长度的速度沿数轴正方向匀速运动，设运动时间为t秒．
（1）分别求当t＝2及t＝12时，对应的线段PQ的长度；
（2）当PQ＝5时，求所有符合条件的t的值，并求出此时点Q所对应的数；
（3）若点P一直沿数轴的正方向运动，点Q运动到点B时，立即改变运动方向，沿数轴的负方向运动，到达点A时，随即停止运动，在点Q的整个运动过程中，是否存在合适的t值，使得PQ＝8？若存在，求出所有符合条件的t值，若不存在，请说明理由．
26．（11分）如图1，点O是弹力墙MN上一点，魔法棒从OM的位置开始绕点O向ON的位置顺时针旋转，当转到ON位置时，则从ON位置弹回，继续向OM位置旋转；当转到OM位置时，再从OM的位置弹回，继续转向ON位置，…，如此反复．按照这种方式将魔法棒进行如下步骤的旋转：第1步，从OA0（OA0在OM上）开始旋转α至OA1；第2步，从OA1开始继续旋转2α至OA2；第3步，从OA2开始继续旋转3α至OA3，…．
图1
图2
例如：
当α＝30°时，OA1，OA2，OA3，OA4的位置如图2所示，其中OA3恰好落在ON上，∠A3OA4＝120°；
当α＝20°时，OA1，OA2，OA3，OA4，OA5的位置如图3所示，
其中第4步旋转到ON后弹回，即∠A3ON+∠NOA4＝80°，而OA5恰好与OA2重合．
图3
图4
解决如下问题：
（1）若α＝35°，在图4中借助量角器画出OA2，OA3，其中∠A3OA2的度数是 ；
（2）若α＜30°，且OA4所在的射线平分∠A2OA3，在如图5中画出OA1，OA2，OA3，OA4并求出α的值；
图5
（3）若α＜36°，且∠A2OA4＝20°，则对应的α值是 ．